Teorema del límite central
Sean $X_1, X_2, \ldots, X_n$ variables aleatoria iid con media
$\mathbb{E}(X_i) = \mu$ y varianza $Var(X_i)=\sigma^2<\infty$
entonces, si se define a $\bar{X}$ la media muestral con media
$\mathbb{E}(\bar{X}) =\mu$ y varianza
$Var(\bar{X}) = \frac{\sigma^2}{n}$, se tendrá que la variable
aleatoria normalizada
\begin{align*} Z_c = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \stackrel{a}{\sim} N(0,1) \end{align*}
convergerá en distribución a una variable aleatoria normal estándar
cuando $n\to \infty$ (usualmente, se usa como valor de referencia a
$n\geq 30$).
Ejercicio
Suponga que Postobon desarrolla una nueva máquina de bebidas para servir
de forma automática gaseosas en los cines, de tal forma que la cantidad
servida, en mililitros, se distribuya Weibull con parámetro de forma
\(\alpha = 1/5\) y parámetro de escala \(\beta = 3\).
Entonces,
si se decide tomar una muestra aleatoria de \(40\) vasos de gaseosa
servidos por una de las nuevas máquinas de bebidas, cuál es la
probabilidad de que la cantidad promedio de bebida obtenida sea como
máximo de \(340_{ml}\)?.
Solución
En este caso tenemos que la cantidad servida de gaseosa por la nueva
máquina no se distribuye normalmente, si no que tiene una distribución
Weibull, con parámetros \(\alpha = 1/5\) y \(\beta = 3\).
Adicionalmente, nos piden calcular la probabilidad de que una muestra de
\(40\) vasos de gaseosa se obtenga como máximo un promedio muestral de
\(340_{ml}\), es decir \[\begin{align*}
\mathbb{P}(\bar{X} \leq 340)
\end{align*}\]
Entonces, dado que los datos no se distribuyen normalmente, pero el
tamaño de la muestra \(n\geq30\), podemos aplicar el teorema del límite
central el cual nos dice que, mediante la aplicación de la
estandarización \[\begin{align*}
Z_c = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \stackrel{a}{\sim} N(0,1)
\end{align*}\] podemos obtener una distribución aproximadamente normal,
lo cual nos permitirá realizar el cálculo de la probabilidad de
interés.
Ahora, para poder aplicar la estandarización, debemos
calcular primero el valor de la media y desviación estandar
poblacionales, y para ello empleamos podemos emplear la definición de
esperanza matemática y varianza de la distribución Weibull, tal que la
media poblacional será igual a \[\begin{align*}
\mathbb{E}(X) = \mu = &= \beta\;\Gamma\left(1 + \frac{1}{\alpha}\right)\\
&= 3 \Gamma\left(1 + \frac{1}{(1/5)}\right) \\
&= 3 \Gamma\left(1 + 5\right) \\
&= 3 \Gamma\left(6\right) \\
&= 3 (6-1)!\\
&= 3 (120) \\
&= 360
\end{align*}\] mientras que, la varianza poblacional será igual a
\[\begin{align*}
Var(X) = \sigma^2 &= \beta^2\left[\Gamma\left(1 + \frac{2}{\alpha}\right) - \Gamma\left(1 + \frac{1}{\alpha}\right)^2\right] \\
&= 3^2\left[\Gamma\left(1 + \frac{2}{(1/5)}\right) - \Gamma\left(1 + \frac{1}{(1/5)}\right)^2\right] \\
&= 9\left[\Gamma\left(1 + 10\right) - \Gamma\left(1 + 5\right)^2\right] \\
&= 9\left[\Gamma\left(11\right) - \Gamma\left(6\right)^2\right] \\
&= 9\left[(11 - 1)! - ((6 - 1)!)^2\right] \\
&= 9\left[3628800 - (120)^2\right] \\
&= 9\left[3628800 - 14400\right] \\
&= 9\left[3628800 - 14400\right] \\
&= 9\left[3614400\right] \\
&= 32529600
\end{align*}\] es decir que, la desviación estándar poblacional será
igual a \[\begin{align*}
Sd(X) = \sigma &= \sqrt{Var(X)} \\
&= \sqrt{32529600} \\
&= 5703.473
\end{align*}\]
Ahora, con los valores ya calculados para \(\mu=360\) y
\(\sigma=5703.473\), se realiza la estandarización de la probabilidad,
para poder realizar su cálculo, tal que \[\begin{align*}
\mathbb{P}(\bar{X} \leq 340) &= \mathbb{P}(\bar{X} - \mu \leq 340 - 360)\\
&= \mathbb{P}\left(\frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \leq \frac{340 - 360}{5703.473/\sqrt{40}}\right)\\
&= \mathbb{P}\left(Z \leq -0.02217791\right)\\
\end{align*}\]
Y como \(Z \stackrel{a}{\sim} N(0,1)\), podemos encontrar la
probabilidad de interés, empleando la
Tabla
de la Distribución Normal Estándar, la función pnorm() del
software R o la función DISTR.NORM.ESTAND.N() de
Excel, tal que \[\begin{align*}
\mathbb{P}\left(Z \leq -0.02217791\right) = 0.491153
\end{align*}\]
lo cual, dada la equivalencia de la igualdad anterior, significará que
\[\begin{align*}
\mathbb{P}(\bar{X} \leq 340) = 0.491153
\end{align*}\]
es decir que la probabilidad de que la cantidad promedio de bebida
obtenida en la muestra de \(40\) vasos sea como máximo de \(340_{ml}\)
es de \(49.11\%\).
Distribuciones muestrales
Distribución para combinaciones lineales
En estadística aplicada a menudo se necesita conocer la distribución de
probabilidad de una combinación lineal de variables aleatorias
independientes. Y Por ello se presentan a continuación $4$ teoremas
que pueden ser de utilidad
Teorema 1
Sean \(X_1\) y \(X_2\) dos variables aleatorias normalmente distribuidas con media \(\mu\) y varianza \(\sigma^2\). Y si \(Y\) es una combinación lineal de \(X_1\) y \(X_2\), tal que \[\begin{align*} Y = X_1 + X_2 \end{align*}\] entonces, la media de \(Y\) estará dada por \[\begin{align*} \mathbb{E}(Y) = \mu_1 + \mu_2 \end{align*}\] y la varianza de \(Y\) estará dada por \[\begin{align*} Var(Y) = \sigma_{x_1}^2 + \sigma_{x_2}^2 + 2 \sigma_{x_1x_2} \end{align*}\] o en caso de que \(X_1\) y \(X_2\) sean variables aleatorias independientes, entonces se tendrá que la varianza de \(Y\) estará dada por \[\begin{align*} Var(Y) = \sigma_{x_1}^2 + \sigma_{x_2}^2 \end{align*}\]
Teorema 2
Sea \(X_1, X_2, \ldots, X_n\) variables aleatorias independientes, distribuidas normalmente con medias \(\mu_1, \mu_2, \ldots, \mu_n\) y varianzas \(\sigma_1^2, \sigma_2^2, \ldots, \sigma_n^2\), entonces la variable aleatorias \[\begin{align*} Y = a_1 X_1 + a_2 X_2 + \ldots + a_n X_n \end{align*}\] tendrá una distribución Normal, con media \[\begin{align*} \mu_Y = a_1 \mu_1 + a_2 \mu_2 + \ldots + a_n \mu_n \end{align*}\] y varianza \[\begin{align*} \sigma^2_Y = a_1 \sigma^2_1 + a_2 \sigma^2_2 + \ldots + a_n \sigma^2_n \end{align*}\] es decir, \(Y\sim N(\mu_Y, \sigma^2_Y)\).
Teorema 3
Sea \(X_1, X_2, \ldots, X_n\) variables aleatorias mutuamente independientes, que tienen una distribución chi-cuadrado con \(\nu_1, \nu_2, \ldots, \nu_n\) grados de libertad, entonces la variable aleatoria \[\begin{align*} Y = X_1 + X_2 + \ldots + X_n \end{align*}\] tiene una distribución chi-cuadrado con \(\nu = \nu_1 + \nu_2 + \ldots + \nu_n\) grados de libertad, es decir, \(Y\sim \chi^2(\nu)\)
Teorema 3.1
Si \(Y\sim \chi^2_\nu\) entonces se puede probar que la media y varianza de la variable aleatoria \(X\) están dadas por \[\begin{align*} \mathbb{E}(X)=\nu \quad \quad Var(X)=2\nu \end{align*}\]
Teorema 4
Sea \(X_1, X_2, \ldots, X_n\) una muestra aleatoria *iid* de tamaño \(n\), que poseen una distribución \(N(\mu,\sigma^2)\), entonces \[\begin{align*} Z_i = \frac{X_i - \mu}{\sigma} \sim N(0,1) \end{align*}\] para \(i =1,2,\ldots,n\) serán variables aleatorias independientes con distribuciones normales estándar. Además, se tendrá que \[\begin{align*} Z_i^2 = \frac{(X_i - \mu)^2}{\sigma^2} \sim \chi^2_{1} \end{align*}\] serán variables aleatorias independientes con distribuciones chi-cuadrado con \(1\) grado de libertad. Entonces, basados en el Teorema 3 se obtiene que \[\begin{align*} Y = \sum_{i=1}^n Z_i^2 = \sum_{i=1}^n\frac{(X_i-\mu)^2}{\sigma^2} \sim \chi^2_n \end{align*}\] tendrá una distribución chi-cuadrado con \(n\) grados de libertad.
Distribución muestral de $\chi^2$
Sea $X_1, X_2, \ldots, X_n$ una muestra aleatoria iid de una
distribución $N(\mu,\sigma^2)$ de tamaño $n$, entonces partiendo del
Teorema
4 se tendrá que
\begin{align*} \sum_{i=1}^n\frac{(X_i-\mu)^2}{\sigma^2} \sim \chi^2_n \end{align*}
En donde, al sumar y restar $\bar{X}$ dentro de $(X_i-\mu)^2$
tendremos que
\begin{align*} \sum_{i=1}^n\frac{(X_i-\mu)^2}{\sigma^2} &= \sum_{i=1}^n\frac{(X_i - \bar{X} + \bar{X} - \mu)^2}{\sigma^2} \\ &= \sum_{i=1}^n\frac{[(X_i - \bar{X}) + (\bar{X} - \mu)]^2}{\sigma^2} \\ &= \sum_{i=1}^n\frac{(X_i - \bar{X})^2 + 2(X_i - \bar{X})(\bar{X} - \mu) + (\bar{X} - \mu)^2}{\sigma^2} \\ &= \sum_{i=1}^n\frac{(X_i - \bar{X})^2 + 2(X_i - \bar{X})(\bar{X} - \mu) + (\bar{X} - \mu)^2}{\sigma^2} \\ &= \sum_{i=1}^n\frac{(X_i - \bar{X})^2}{\sigma^2} + \sum_{i=1}^n\frac{2(X_i - \bar{X})(\bar{X} - \mu)}{\sigma^2} + \sum_{i=1}^n\frac{(\bar{X} - \mu)^2}{\sigma^2} \\ &= \frac{1}{\sigma^2}\sum_{i=1}^n(X_i - \bar{X})^2 + \frac{2(\bar{X} - \mu)}{\sigma^2}\sum_{i=1}^n(X_i - \bar{X}) + \frac{1}{\sigma^2}\sum_{i=1}^n(\bar{X} - \mu)^2 \end{align*}
De lo anterior se puede demostrar que
$\sum_{i=1}^n(X_i - \bar{X})^2=(n-1)S^2$,
$\sum_{i=1}^n(X_i - \bar{X})=0$ y
$\sum_{i=1}^n(\bar{X} - \mu)^2 = n(\bar{X} - \mu)^2$, lo cual al
reemplazar estos valores en la ecuación anterior, se obtendrá que
\begin{align*} \sum_{i=1}^n\frac{(X_i-\mu)^2}{\sigma^2} &= \frac{(n-1)S^2}{\sigma^2} + \frac{n(\bar{X} - \mu)^2}{\sigma^2} \end{align*}
Entonces, del
Teorema
4 se tiene que
\begin{align*} \sum_{i=1}^n\frac{(X_i-\mu)^2}{\sigma^2}\sim \chi^2_n \quad \quad \text{ y } \quad \quad \frac{(\bar{X} - \mu)^2}{\sigma^2}\sim \chi^2_1 \end{align*}
Por tanto basados en el Teorema 3 se tendrá que
\begin{align*} \chi^2_c = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1} \end{align*}
tiene una distribución chi-cuadrado con $n-1$ grados de libertad.
Propiedades
Si $X_1, X_2, \ldots, X_n$ una muestra aleatoria iid de una
distribución $N(\mu,\sigma^2)$ de tamaño $n$, y se tiene que
$\bar{X}$ y $S^2$ son la media y varianza muestrales, entonces
- Las variables aleatorias
$\bar{X}$y$S^2$son independientes. - la esperanza y la varianza de la variable aleatoria
$S^2$estarán dadas por\begin{align*} \mathbb{E}(S^2)= \sigma^2 \quad \text{ y } \quad Var(S^2) = \frac{2(\sigma^2)^2}{n-1} \end{align*}
Ejercicio
Suponga que poseemos una distribución chi-cuadrado con \(\nu\) grados de libertad. Entonces, a partir de esta distribución y empleando la Tabla de la Distribución Chi-Cuadrado, calcule
- \(\mathbb{P}(\chi^2_5 > 3)\)
- \(\mathbb{P}(\chi^2_{20} \leq 37.566)\)
- \(\mathbb{P}(9.034 < \chi^2_{12} \leq 15.812)\)
- \(\mathbb{P}(\chi^2_{8} < x) = 0.10\)
Solución
Para calcular probabilidades con la tabla de la distribución chi-cuadrado, es necesario tener en cuenta el funcionamiento de la tabla misma. Y para ello se presenta la siguiente imagen.
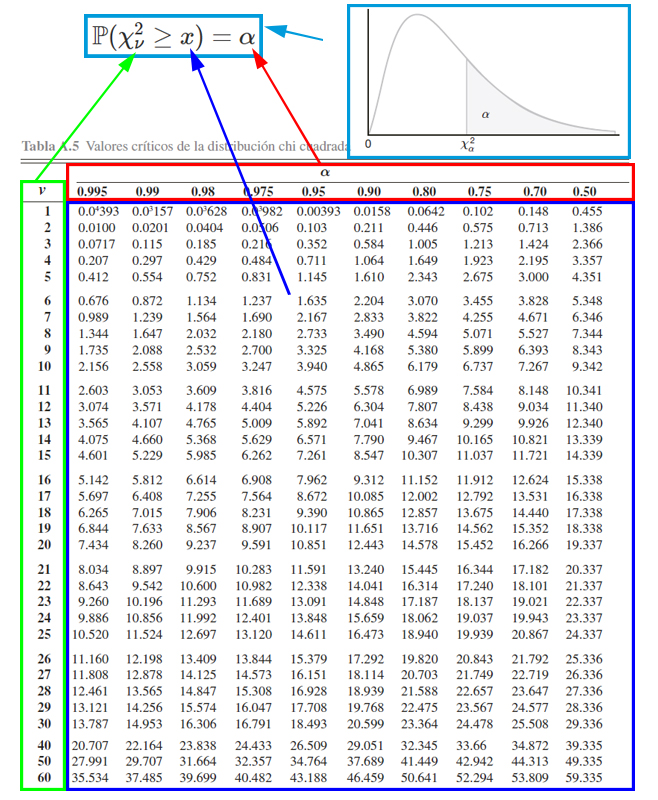
En donde, se aprecia que, el cuadro azul representan los valores críticos \(x\) que se emplea para calcular probabilidades. El cuadro rojo representa las probabilidades \(\alpha\) que se desean calcular a partir de los valores críticos. El cuadro verde representa los grados de libertad \(\nu\) que se emplean para calcular probabilidades junto al empleo de los valores críticos. Finalmente, el cuadro azul claro representa el funcionamiento de la tabla , la cual muestra las probabilidades que poseen la forma \(\mathbb{P}(\chi_\nu^2\geq x)=\alpha\).
-
Con la explicación de la tabla en mente, la primera probabilidad a
calcular es \(\mathbb{P}(\chi^2_5 > 3)\). Entonces como esta
probabilidad tiene la estructura establecida por la tabla
\(\mathbb{P}(\chi_\nu^2\geq x)\), será cuestión de buscar para \(5\)
grados de libertad, el valor crítico \(3\) para localizar la
probabilidad asociada, tal que se busca en la parte izquierda, los
grados de libertad \(5\), y en la parte central (siguiendo la misma fila
en la cual se encontraron los grados de libertad) se busca el valor
crítico \(3\). Una vez ubicado el valor crítico, se busca cuál es la
probabilidad de interés asociada al valor crítico y grados de libertad,
en la parte superior. Dicho procedimiento se muestra en la siguiente
imagen
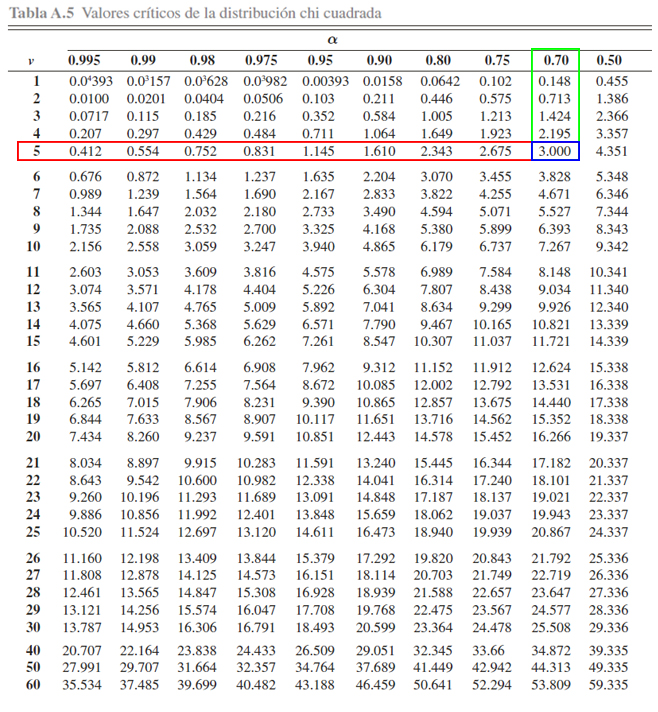 Donde se aprecia que
\[\begin{align*}\mathbb{P}(\chi^2_5 > 3)=0.70\end{align*}\]
Donde se aprecia que
\[\begin{align*}\mathbb{P}(\chi^2_5 > 3)=0.70\end{align*}\]
-
A diferencia del punto anterior, observamos que la probabilidad
propuesta \(\mathbb{P}(\chi^2_{20} \leq 37.566)\) tiene una estructura
diferente a la establecida por la tabla
\(\mathbb{P}(\chi_\nu^2\geq x)\), y por tanto, será necesario emplear el
complemento de la probabilidad propuesta para obtener una estructura
similar a la propuesta por la tabla, tal que
\[\begin{align*}
\mathbb{P}(\chi^2_{20} \leq 37.566) = 1 - \mathbb{P}(\chi^2_{20} > 37.566)
\end{align*}\] En donde, se aprecia que ahora podemos calcular la
\(\mathbb{P}(\chi^2_{20} \leq 37.566)\), mediante el empleo de la
\(\mathbb{P}(\chi^2_{20} > 37.566)\), la cual podemos buscar en la tabla
directamente. Para localizar \(\mathbb{P}(\chi^2_{20} > 37.566)\), se
buscan los grados de libertad \(20\) en la parte izquierda de la tabla,
y el valor crítico en la parte central de la tabla (siguiendo la misma
fila en la cual se encontraron los grados de libertad). Una vez ubicado
el valor crítico, se busca en la parte superior cuál es la probabilidad
de interés asociada al valor crítico y grados de libertad.
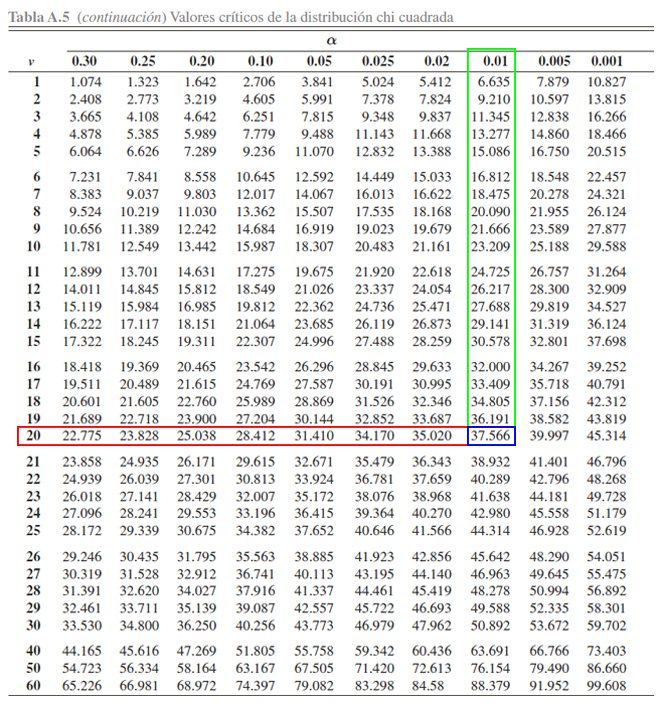 Donde se aprecia que
\[\begin{align*}
\mathbb{P}(\chi^2_{20} > 37.566) = 0.01
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(\chi^2_{20} \leq 37.566) &= 1 - \mathbb{P}(\chi^2_{20} > 37.566)\\
&= 1 - 0.01 \\
&= 0.99
\end{align*}\]
Donde se aprecia que
\[\begin{align*}
\mathbb{P}(\chi^2_{20} > 37.566) = 0.01
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(\chi^2_{20} \leq 37.566) &= 1 - \mathbb{P}(\chi^2_{20} > 37.566)\\
&= 1 - 0.01 \\
&= 0.99
\end{align*}\]
-
En este caso, se desea calcular la
\(\mathbb{P}(9.034 < \chi^2_{12} \leq 15.812)\), y se observa que la
estructura de dicha probabilidad es diferente a la establecida por la
tabla \(\mathbb{P}(\chi_\nu^2\geq x)\), pero también podemos apreciar
que si aplicamos las propiedades de la función de distribución acumulada
para el caso continuo, ya presentadas en la
Clase
08, y posteriormente calculamos el complemento de las
probabilidades, podemos llevar la probabilidad de interés a la forma
\[\begin{align*}
\mathbb{P}(9.034 < \chi^2_{12} \leq 15.812) &= \mathbb{P}(\chi^2_{12} \leq 15.812) - \mathbb{P}(\chi^2_{12} \leq 9.034) \\
&= [1 - \mathbb{P}(\chi^2_{12} > 15.812)] - [1- \mathbb{P}(\chi^2_{12} > 9.034)] \\
&= \mathbb{P}(\chi^2_{12} > 9.034) - \mathbb{P}(\chi^2_{12} > 15.812)
\end{align*}\] obteniendo que la probabilidad
\(\mathbb{P}(9.034 < \chi^2_{12} \leq 15.812)\), puede calcularse
mediante el empleo de las probabilidades
\(\mathbb{P}(\chi^2_{12} > 9.034)\) y
\(\mathbb{P}(\chi^2_{12} > 15.812)\), las cuales pueden calcularse en la
tabla de forma similar a los dos puntos anteriores.
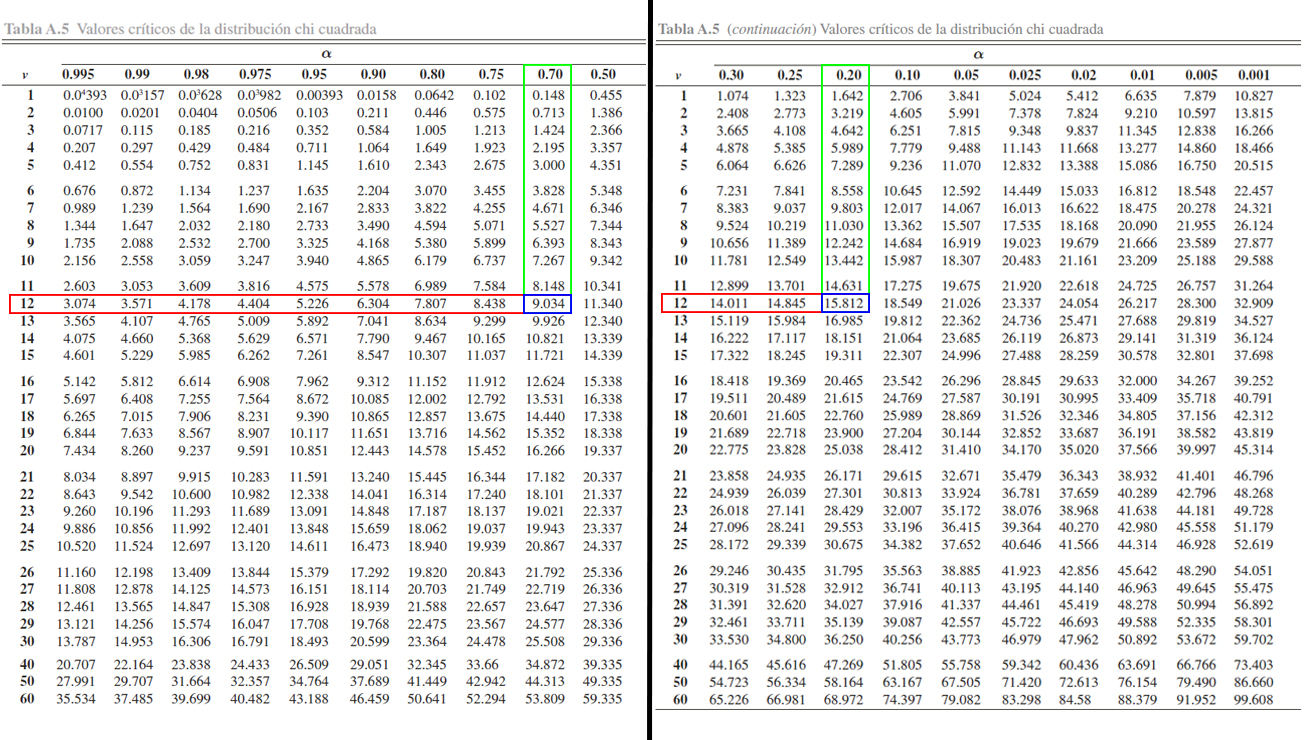 Donde se aprecia que
\[\begin{align*}
\mathbb{P}(\chi^2_{12} > 9.034)=0.70 \quad \text{ y } \quad \mathbb{P}(\chi^2_{12} > 15.812)=0.20
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(9.034 < \chi^2_{12} \leq 15.812) &= \mathbb{P}(\chi^2_{12} > 9.034) - \mathbb{P}(\chi^2_{12} > 15.812)\\
&= 0.70 - 0.20 \\
&= 0.50
\end{align*}\]
Donde se aprecia que
\[\begin{align*}
\mathbb{P}(\chi^2_{12} > 9.034)=0.70 \quad \text{ y } \quad \mathbb{P}(\chi^2_{12} > 15.812)=0.20
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(9.034 < \chi^2_{12} \leq 15.812) &= \mathbb{P}(\chi^2_{12} > 9.034) - \mathbb{P}(\chi^2_{12} > 15.812)\\
&= 0.70 - 0.20 \\
&= 0.50
\end{align*}\]
-
En este punto, a diferencia de los puntos anteriores, nos dan el valor
de la probabilidad y nos piden encontrar el valor crítico \(x\), dado
unos grados de libertad. Es decir debemos calcular el valor crítico
asociado a la probabilidad \[\begin{align*}
\mathbb{P}(\chi^2_{8} < x) = 0.10
\end{align*}\]
Y para ello, debemos llevar inicialmente la estructura de la
probabilidad, a la estructura manejada por la tabla, tal que
\[\begin{align*}
\mathbb{P}(\chi^2_{8} < x) = 0.10 \\
1 - \mathbb{P}(\chi^2_{8} \leq x) = 0.10 \\
1- 0.10 &= \mathbb{P}(\chi^2_{8} \leq x) \\
0.90 &= \mathbb{P}(\chi^2_{8} \leq x)
\end{align*}\]
En donde observamos que la probabilidad
\(\mathbb{P}(\chi^2_{8} \leq x)\) ya posee la estructura de la tabla, y
en consecuencia, podemos proceder a encontrar el valor crítico \(x\),
buscando los \(8\) grados de libertad en la parte izquierda de la tabla,
y la probabilidad \(0.90\) de la parte superior de la tabla, y luego
buscar el valor crítico \(x\) asociado a dicha probabilidad y grados de
libertad, en el cruce de los dos valores anteriormente encontrados.
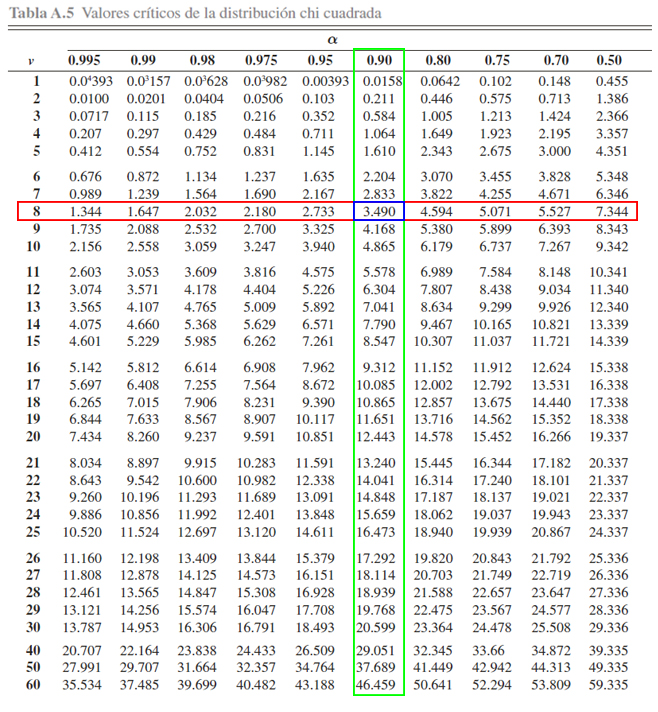 En la tabla se aprecia, que al buscar el cruce entre la probabilidad
\(0.90\) y los \(8\) grados de libertad, encontramos que el valor
crítico \(x\) asociado es de \(3.490\), es decir
\[\begin{align*}
\mathbb{P}(\chi^2_{8} \leq 3.490) &= 0.90
\end{align*}\]
o equivalentemente
\[\begin{align*}
\mathbb{P}(\chi^2_{8} < 3.490) &= 0.10
\end{align*}\]
En la tabla se aprecia, que al buscar el cruce entre la probabilidad
\(0.90\) y los \(8\) grados de libertad, encontramos que el valor
crítico \(x\) asociado es de \(3.490\), es decir
\[\begin{align*}
\mathbb{P}(\chi^2_{8} \leq 3.490) &= 0.90
\end{align*}\]
o equivalentemente
\[\begin{align*}
\mathbb{P}(\chi^2_{8} < 3.490) &= 0.10
\end{align*}\]
Ejercicio
Durante los últimos cinco años se ha realizado en la facultad de
ingeniería un exámen a estudiantes de primer y segundo semestre para
observar la finidad de éstos con la carrera que se encuentran cursando.
Los directivos creen por estudios anteriores, que la calificación
obtenida por los estudiantes es aproximadamente normal con media de
\(72\) y varianza de \(5\) puntos.
Si estre semestre se
realiza el examen a \(26\) estudiantes ¿Encuentre la probabilidad de que
se obtenga una la desviación estándar muestral superior a \(2.828427\)
puntos?
Solución
En este punto estamos interesados en calcular la probabilidad de que la desviación estándar de la calificación obtenida por una muestra de \(26\) estudiantes de primero y segundo semestre de la facultad de ingeniería, en el exámen, sea superior a \(2.828427\) puntos, esto es \[\begin{align*} \mathbb{P}(S > 2.828427) \end{align*}\] Pero al no conocer la distribución de probabilidad de la desviación estándar, debemos realizar operaciones matemáticas de tal forma que llevemos la probabilidad planteada, a una estructura en la cual tengamos conocimiento de cuál es la distribución de probabilidad asociada, para el cálculo de la probabilidad, la cual en este caso, sería una distribución chi-cuadrado, tal que \[\begin{align*} \chi^2_c = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1} \end{align*}\] Con esto en mente, desarrollamos las siguienteso operaciones matemáticas \[\begin{align*} \mathbb{P}(S > 2.828427) &= \mathbb{P}(S^2 > 2.828427^2)\\ &= \mathbb{P}((n-1) S^2 > (26-1)2.828427^2)\\ &= \mathbb{P}\left(\frac{(n-1) S^2}{\sigma^2} > \frac{(25)2.828427^2}{5}\right) \\ &= \mathbb{P}(\chi^2_{25} > 40) \\ \end{align*}\] Entonces, como la distribución asociada es una chi cuadrado con \(25\) grados de libertad, \(\chi^2_{25}\), entonces podemos encontrar la probabilidad de interés, empleando la Tabla de la Distribución Chi-Cuadrado, la función pchisq() del software R o las funciones DISTR.CHICUAD() o DISTR.CHICUAD.CD() de Excel, tal que \[\begin{align*} \mathbb{P}(\chi^2_{25} > 40) = 0.0291644 \end{align*}\] lo cual, dada la equivalencia de la igualdad anterior, significará que \[\begin{align*} \mathbb{P}(S > 2.828427) = 0.0291644 \end{align*}\] es decir, se tendrá un \(2.92\%\) de probabilidad de que la desviación estándar de la calificación obtenida por una muestra de \(26\) estudiantes de primero y segundo semestre de la facultad de ingeniería, en el exámen, sea superior a \(2.828427\) puntos.
Distribución muestral $t$ de Student
Sea $Z$ una variable aleatoria distribuida $N(0,1)$ y $W$ una
variable aleatoria distribuida $\chi^2_v$, entonces si $Z$ y
$W$son independientes, se tendrá que
\begin{align*} t = \frac{Z}{\sqrt{W/v}} \sim t_v \end{align*} tiene
una distribución $t$ con $v$ grados de libertad.
Ahora, si $X_1, X_2, \ldots, X_n$ es una muestra aleatoria de una
población normal con media $\mu$ y varianza $\sigma^2$, se tendrá
\begin{align*} Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1) \quad \text{ y } \quad W =\frac{(n-1)S^2}{\sigma^2}\sim \chi^2_{n-1} \end{align*}
serán variables aleatorias independientes puesto que $\bar{X}$ y
$S^2$ son independientes, entonces
\begin{align*} t = \frac{\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}}{\sqrt{\left(\frac{(n-1)S^2}{\sigma^2}\right)/(n-1)}} \end{align*}
obteniendo como resultado luego de simplificar
\begin{align*} t_c = \frac{\bar{X}-\mu}{S/\sqrt{n}} \sim t_{n-1} \end{align*}
tiene una distribución $t$ con $(n-1)$ grados de libertad.
Ejercicio
Suponga en esta ocasión, que tenemos una distribución \(t\) con \(\nu\) grados de libertad. Entonces, usando esta distribución y empleando la Tabla de la Distribución t de Student, calcule
- \(\mathbb{P}(t_{14} > 1.076)\)
- \(\mathbb{P}(t_{7} \leq 3.53)\)
- \(\mathbb{P}(0.862 < t_{18} \leq 2.214)\)
- \(\mathbb{P}(t_{10} \geq t) = 0.01\)
Solución
Para calcular probabilidades con la tabla de la distribución \(t\), es necesario tener en cuenta el funcionamiento de la tabla misma. Y para ello se presenta la siguiente imagen.
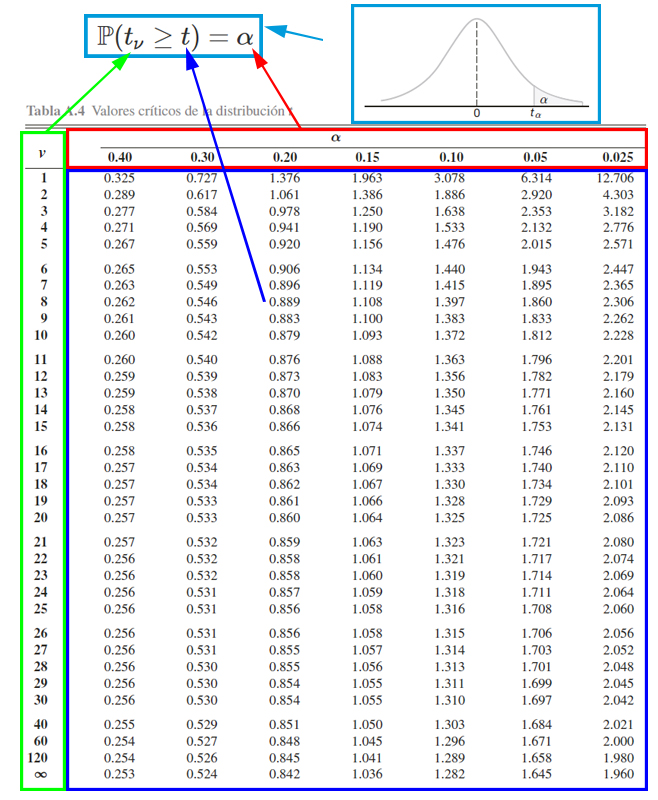
En donde, se aprecia que, el cuadro azul representan los valores críticos \(t\) que se emplea para calcular probabilidades. El cuadro rojo representa las probabilidades \(\alpha\) que se desean calcular a partir de los valores críticos. El cuadro verde representa los grados de libertad \(\nu\) que se emplean para calcular probabilidades junto al empleo de los valores críticos. Finalmente, el cuadro azul claro representa el funcionamiento de la tabla , la cual muestra las probabilidades que poseen la forma \(\mathbb{P}(t_\nu\geq t)=\alpha\).
-
Conocida el funcionamiento de la tabla, la primera probabilidad a
calcular es \(\mathbb{P}(t_{14} > 1.076)\), la cual tiene la estructura
establecida por la tabla \(\mathbb{P}(t_\nu\geq t)\), así que será
cuestión de buscar para \(14\) grados de libertad, el valor crítico
\(1.076\) para localizar la probabilidad asociada.
Para ello, se busca en la parte izquierda, los grados de libertad \(14\), y en la parte central (siguiendo la misma fila en la cual se encontraron los grados de libertad) se busca el valor crítico \(1.076\). Una vez ubicado el valor crítico, se busca cuál es la probabilidad de interés asociada al valor crítico y grados de libertad, en la parte superior. Dicho procedimiento se ilustra a continuación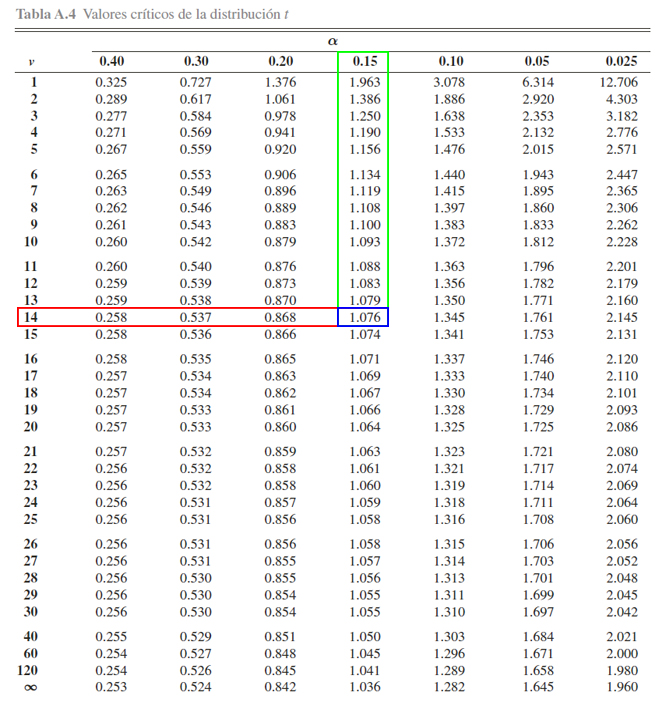 Donde se aprecia que
\[\begin{align*}\mathbb{P}(t_{14} > 1.076)=0.15\end{align*}\]
Donde se aprecia que
\[\begin{align*}\mathbb{P}(t_{14} > 1.076)=0.15\end{align*}\]
-
A diferencia del punto anterior, se observa que la probabilidad
propuesta en este caso es de la forma \(\mathbb{P}(t_{7} \leq 3.53)\),
la cual posee una estructura diferente a la establecida por la tabla
\(\mathbb{P}(t_\nu\geq t)\), por lo cual, será necesario emplear el
complemento de la probabilidad propuesta, para obtener una estructura
similar a la que maneja la tabla, tal que
\[\begin{align*}
\mathbb{P}(t_{7} \leq 3.53) = 1 - \mathbb{P}(t_{7} > 3.5)
\end{align*}\]
Una vez empleado el complemento, podemos emplear la probabilidad
\(\mathbb{P}(t_{7} > 3.5)\) para calcular la probabilidad de interés,
mediante la búsqueda de la probabilidad, tal como se hizo en el
ejercicio anterior. En donde, se localizan los \(7\) grados de libertad
en la parte izquierda de la tabla, y siguiendo la misma fila de los
grados de libertad, se localiza el valor crítico de interés, lo cual, al
buscar en la parte superior nos dirá cuál es la probabilidad asociada al
valor crítico de interés y los grados de libertad.
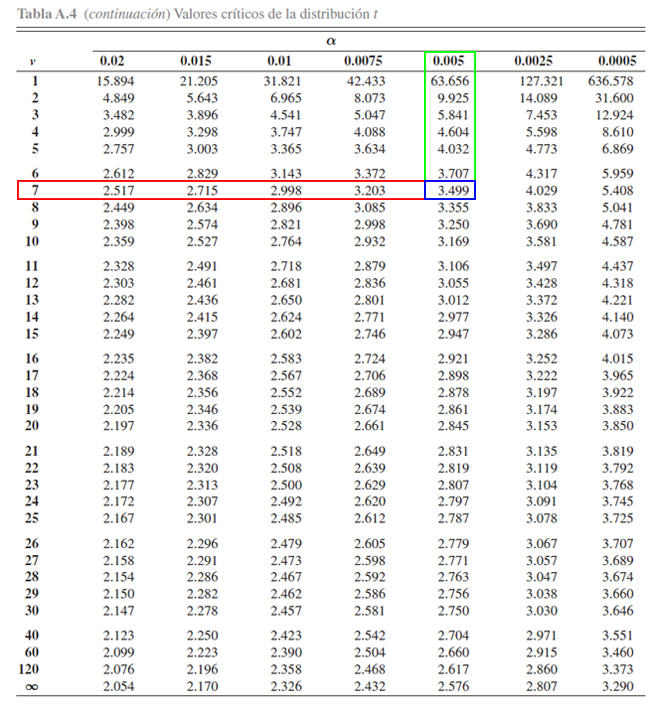 Donde se aprecia que, a pesar de no ser exacto, es el valor más
aproximado
\[\begin{align*}
\mathbb{P}(t_{7} > 3.53) \approx 0.005
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(t_{7} \leq 3.53) &\approx 1 - \mathbb{P}(t_{7} > 3.5)\\
&\approx 1 - 0.005 \\
&\approx 0.995
\end{align*}\]
Donde se aprecia que, a pesar de no ser exacto, es el valor más
aproximado
\[\begin{align*}
\mathbb{P}(t_{7} > 3.53) \approx 0.005
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(t_{7} \leq 3.53) &\approx 1 - \mathbb{P}(t_{7} > 3.5)\\
&\approx 1 - 0.005 \\
&\approx 0.995
\end{align*}\]
-
En este ejercicio, nos piden calcular la
\(\mathbb{P}(0.862 < t_{18} \leq 2.214)\), y se observa que la
estructura de dicha probabilidad es diferente a la establecida por la
tabla \(\mathbb{P}(t_\nu\geq t)\), Pero se aprecia que si aplicamos las
propiedades de la función de distribución acumulada para el caso
continuo, ya presentadas en la
Clase
08, y posteriormente calculamos el complemento de las
probabilidades, podemos llevar la probabilidad de interés a la forma
\[\begin{align*}
\mathbb{P}(0.862 < t_{18} \leq 2.214) &= \mathbb{P}(t_{18} \leq 2.214) - \mathbb{P}(t_{18} \leq 0.862) \\
&= [1 - \mathbb{P}(t_{18} > 2.214)] - [1- \mathbb{P}(t_{18} > 0.862)] \\
&= \mathbb{P}(t_{18} > 0.862) - \mathbb{P}(t_{18} > 2.214)
\end{align*}\] obteniendo que la probabilidad
\(\mathbb{P}(0.862 < t_{18} \leq 2.214)\), puede ser calculada mediante
el empleo de las probabilidades \(\mathbb{P}(t_{18} > 0.862)\) y
\(\mathbb{P}(t_{18} > 2.214)\), las cuales se calculan en la tabla de
forma similar a los dos puntos anteriores.
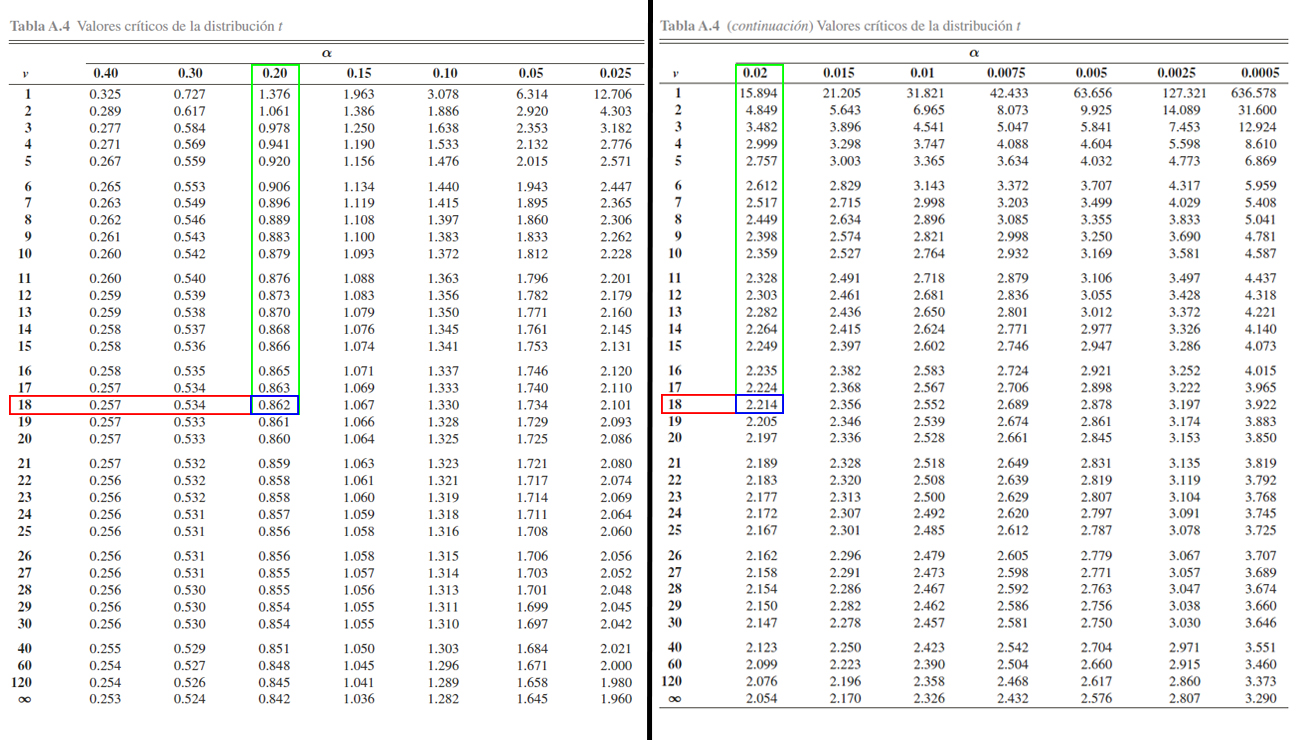 Donde se aprecia que
\[\begin{align*}
\mathbb{P}(t_{18} > 0.862)=0.20 \quad \text{ y } \quad \mathbb{P}(t_{18} > 2.214)=0.02
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(0.862 < t_{18} \leq 2.214) &= \mathbb{P}(t_{18} > 0.862) - \mathbb{P}(t_{18} > 2.214)\\
&= 0.20 - 0.02 \\
&= 0.18
\end{align*}\]
Donde se aprecia que
\[\begin{align*}
\mathbb{P}(t_{18} > 0.862)=0.20 \quad \text{ y } \quad \mathbb{P}(t_{18} > 2.214)=0.02
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(0.862 < t_{18} \leq 2.214) &= \mathbb{P}(t_{18} > 0.862) - \mathbb{P}(t_{18} > 2.214)\\
&= 0.20 - 0.02 \\
&= 0.18
\end{align*}\]
-
En este punto, a diferencia de los puntos anteriores, nos están dando el
valor de la probabilidad, junto a los grados de libertad y nos piden
encontrar el valor crítico \(t\) asociado a dichos valores, tal que
\[\begin{align*}
\mathbb{P}(t_{10} \geq t) = 0.01
\end{align*}\]
Como observamos que la probabilidad de interés ya posee la estructura de
la tabla \(\mathbb{P}(t_\nu\geq t)\), entonces podemos encontrar el
valor crítico de forma directa, buscando en la parte izquierda de la
tabla los grados de libertad \(10\) y en la parte superior de la tabla
la probabilidad \(0.01\), con el fin de localizar el valor crítico en el
cual se cruza la probabilidad y los grados de libertad, tal como se
ilustra en la siguiente imagen
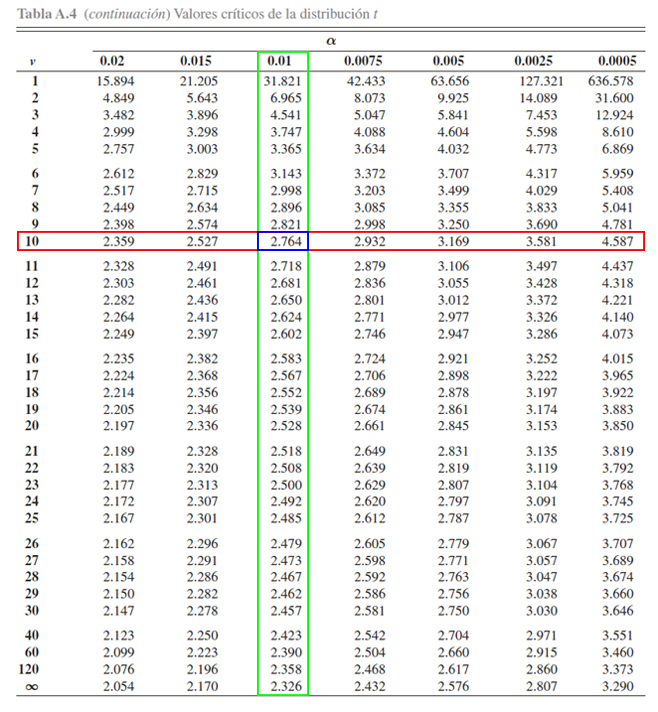 En donde se evidencia, que el valor crítico \(t\) asociado a una
probabilidad de \(0.01\) y a \(10\) grados de libertad, es igual a
\(2.764\), es decir
\[\begin{align*}
\mathbb{P}(t_{10} \geq 2.764) = 0.01
\end{align*}\]
En donde se evidencia, que el valor crítico \(t\) asociado a una
probabilidad de \(0.01\) y a \(10\) grados de libertad, es igual a
\(2.764\), es decir
\[\begin{align*}
\mathbb{P}(t_{10} \geq 2.764) = 0.01
\end{align*}\]
Ejercicio
Suponga que la marca de cigarrillo Malboro, asegura que el contenido
promedio de nicotina de sus cigarrillos es de \(1.1\) miligramos. Un
estudio realizado por un grupo de investigación de la Universidad de
Antioquia mide el contenido de nicotina de una muestra aleatoria de
\(25\) cigarrillos y encuentra que la nicotina promedio y desviación
estándar de la muestra fue de \(1.02\) y \(0.23\) miligramos de
nicotina, respectivamente.
Si se supone que la cantidad de
nicotina en los cigarrillos Malboro se distribuye normalmente, cuál es
la probabilidad de que el promedio muestral sea como máximo el
encontrado por el grupo de investigación de la Universidad de Antioquia,
si se asume como cierta la afirmación de Malboro?
Solución
En este punto, nos preguntan sobre la probabilidad de que el promedio muestral \(\bar{X}\) sea como máximo el encontrado por el grupo de investigación, es decir que se desea calcular la siguiente probabilidad \[\begin{align*} \mathbb{P}(\bar{X} \leq 1.02) \end{align*}\] En donde sabemos que la distribución de probabilidad de la media muestral \(\bar{X} \sim N(\mu, \sigma^2/n)\), por lo cual podríamos calcular directamente la probabilidad de interés, en caso de que conocieramos la varianza poblacional, pero al no ser nuestro caso, debemos realizar operaciones matemáticas con el fin de llevar la probabilidad de interés, a una forma conocida, tal como lo es la estructura de una distribución \(t\) con \(n-1\) grados de libertad, tal que \[\begin{align*} t_c = \frac{\bar{X}-\mu}{S/\sqrt{n}} \sim t_{n-1} \end{align*}\] En donde tenemos que la distribución de la nicotina de los cigarrillos se distribuye normalmente con una media poblacional \(\mu = 1.1\), la cual es la asegurada por la compañia Malboro, Además de la muestra, encontramos que la desviación estándar muestral para las \(n=25\) cigarrillos muestreados es igual a \(S=0.23\) miligramos de nicotina. Basados en estas variables realizamos las siguientes operaciones matemáticas para llevar la probabilidad original, a la estructura planteada, tal que \[\begin{align*} \mathbb{P}(\bar{X} \leq 1.02) &= \mathbb{P}(\bar{X} - \mu \leq 0.82 - 1.1) \\ &= \mathbb{P}\left(\frac{\bar{X} - \mu}{S/\sqrt{n}} \leq \frac{1.02 - 1.1}{0.23/\sqrt{25}}\right) \\ &= \mathbb{P}\left(t_{25-1} \leq -1.73913\right) \end{align*}\] entonces podemos encontrar la probabilidad de interés, empleando la Tabla de la Distribución t de Student, la función pt() del software R o las funciones DISTR.T.N() o DISTR.T.CD() de Excel, tal que \[\begin{align*} \mathbb{P}\left(t_{25-1} \leq -1.73913\right) = 0.04741239 \end{align*}\] lo cual, dada la equivalencia de la igualdad anterior, significará que \[\begin{align*} \mathbb{P}(\bar{X} \leq 1.02) = 0.04741239 \end{align*}\] es decir que la probabilidad de obtener una media muestral inferior a \(1.02\) miligramos de nicotína en una muestra de \(25\), es de \(4.74\%\), si el verdadero valor de la media de nicotina de todos los cigarrillos producidos por la empresa Malboro es de \(1.1\). Por lo cual parecería poco probable que la afirmación de la compañía sea poco creíble.
Distribución muestral $F$ de Fisher-Snedecor
Sea $W_1$ una variable aleatoria $\chi^2_{v_1}$ y $W_2$ una
variable aleatoria $\chi^2_{v_2}$, entonces si $W_1$ y $W_2$ son
independientes.
\begin{align*} F = \frac{W_1/v_1}{W_2/v_2}\sim F_{v_1, v_2} \end{align*}
tiene una distribución $F$ con $v_1$ grados de libertad en el
númerador y $v_2$ grados de libertad en el denominador. Ahora si
$X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_2}$ son dos muestras aleatorias
independientes de poblaciones normales con medias $\mu_1, \mu_2$ y
varianzas $\sigma^2_1, \sigma^2,2$, respectivamente, entonces
\begin{align*} W_1 = \frac{(n_1-1)S_1^2}{\sigma^2_1} \sim N(0,1) \quad \text{ y } \quad W_2 =\frac{(n_1-1)S_1^2}{\sigma^2_1}\sim \chi^2_{n_2-1} \end{align*}
tienen distribuciones chi-cuadrado independientes con $v_1=(n_1-1)$ y
$v_2 = (n_2-1)$ grados de libertad, respectivamente. Y por tanto
\begin{align*} F = \frac{\left(\frac{(n_1-1)S_1^2}{\sigma^2_1}\right)/(n_1-1)}{\left(\frac{(n_1-1)S_1^2}{\sigma^2_1}\right)/(n_2-1)} = \frac{S_1^2/\sigma^2_1}{S_2^2/\sigma^2_2} \end{align*}
En donde, al reordenar términos se tendrá que
\begin{align*} F_c = \frac{S^2_1\sigma^2_2}{S^2_2\sigma^2_1} \sim F_{n_1-1, n_2-1} \end{align*}
tienen una distribución $F$ con $n_1-1$ grados de libertad en el
numerador y $n_2-1$ grados de libertad en el denominador.
Teorema Cola Izquierda
Para encontrar la probabilidad de la cola izquierda para $\alpha$ de
la distribución F, usamos la siguiente formula
\begin{align*} F_{1-\alpha,v_1,v_2} = \frac{1}{F_{\alpha, v_2, v_1}} \end{align*}
Ejercicio
Suponga que en esta ocasión, tenemos una distribución \(F\) de Snedecor con \(\nu_1\) grados de libertad en el numerador y \(nu_2\) grados de libertad en el denominador. Entonces, usando esta distribución y empleando la Tabla de la Distribución F de Fisher-Snedecor, calcule
- \(\mathbb{P}(F_{8, 12} \geq 3)\)
- \(\mathbb{P}(F_{10, 6} \leq 0.18)\)
- \(\mathbb{P}(0.31 < F_{15, 5} \leq 9.6)\)
- \(\mathbb{P}(F_{12, 12} \geq f) = 0.05\)
Solución
La tabla de la distribución \(F\) es usualmente la más complicada de manejar, debido a que para cada probabilidad se tendrá una tabla diferente, debido a que ésta depende de dos grados de libertad diferentes. Entonces para calcular probabilidad con la tabla de la distribución \(F\) de Snedecor, es necesario tener en cuenta el funcionamiento de la tabla misma. Y para ello se presenta la siguiente imagen.
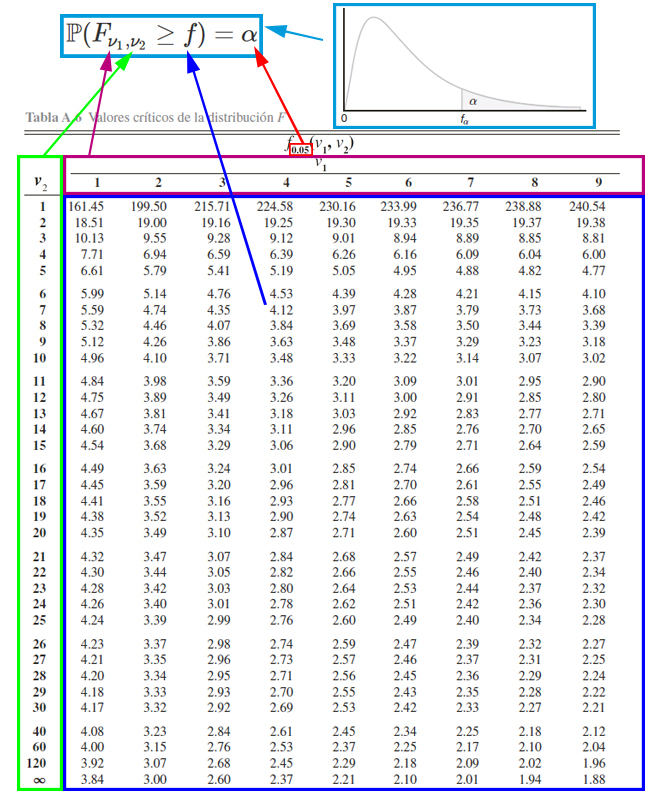
En donde, se aprecia que, el cuadro azul representan los valores críticos \(f\) que se emplea para calcular probabilidades. El cuadro rojo pequeño representa las probabilidades \(\alpha\) que se desean calcular a partir de los valores críticos y el cruce de los grados de libertad. El cuadro morado representa los grados de libertad del numerador \(\nu_1\) que se emplean para calcular probabilidades junto al empleo de los valores críticos y los grados de libertad del denominador. El cuadro verde representa los grados de libertad del denominador \(\nu_2\) que se emplean para calcular probabilidades junto al empleo de los valores críticos y los grados de libertad del numerador. Finalmente, el cuadro azul claro representa el funcionamiento de la tabla, la cual muestra las probabilidades que poseen la forma \(\mathbb{P}(F_{\nu_1, \nu_2}\geq f)=\alpha\).
-
Conocida el funcionamiento de la tabla, la primera probabilidad a
calcular es \(\mathbb{P}(F_{8, 12} \geq 3)\), la cual tiene la
estructura establecida por la tabla
\(\mathbb{P}(F_{\nu_1, \nu_2}\geq f)\), así que será cuestión de buscar
los valores críticos asociados al cruce entre \(\nu_1 = 8\) los grados
de libertad en el numerador y \(\nu_2 = 12\) los grados de libertad en
el denominador, para para comparar dichos valores con respecto al valor
crítico de interés \(3\).
Para tanto, se localiza en cada una de las tablas en la parte superior los grados de libertad del numerador \(8\), en la parte izquierda los grados de libertad del denominador \(14\), y en la parte central se busca el cruce de los dos grados de libertad para observar cuál es el valor crítico asociado a este. Dicho procedimiento se ilustra en el siguiente gráfico, en donde, en la parte izquierda se muestra el valor crítico de la tabla \(F_{0.05}\) y en la parte derecha el valor crítico de la tabla para \(F_{0.01}\).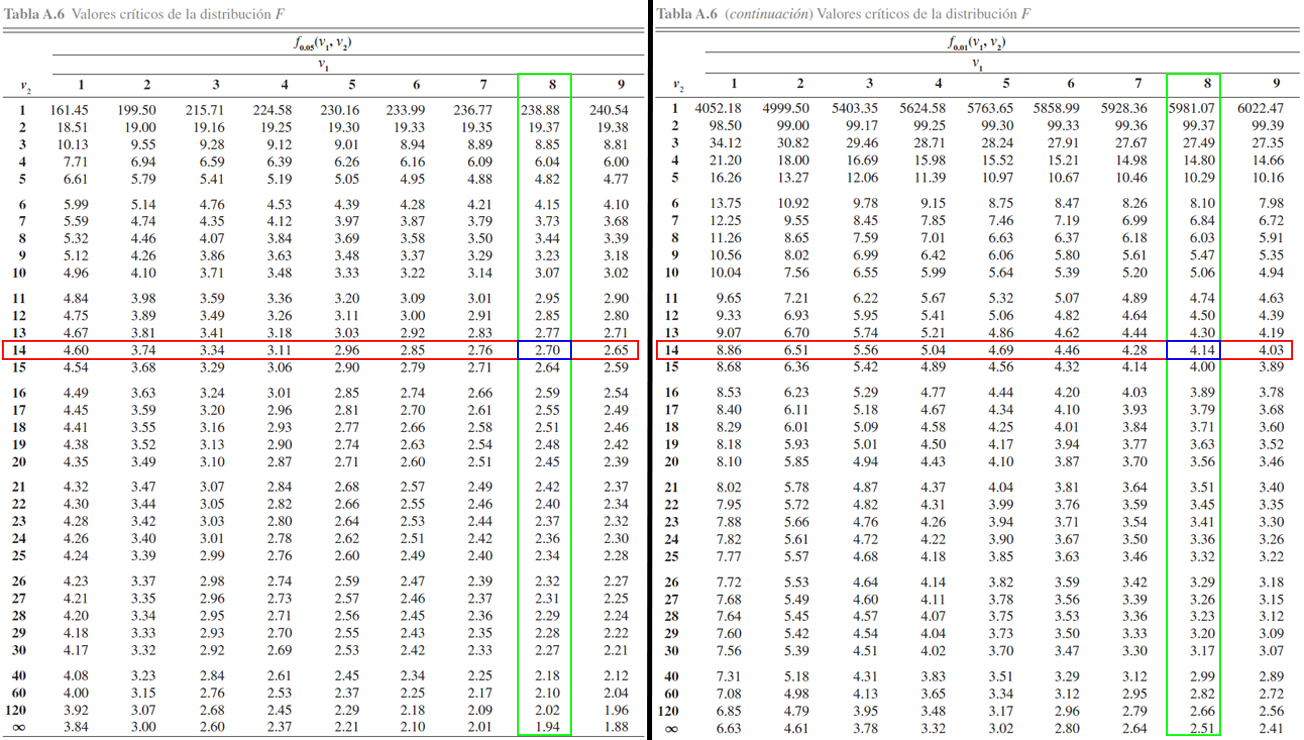 En donde se evidencia que \[\begin{align*}
F_{0.05, 8, 14} = 2.70 \quad => \quad \mathbb{P}(F_{8, 14} \geq 2.70) = 0.05\\
F_{0.01, 8, 14} = 4.14 \quad => \quad \mathbb{P}(F_{8, 14} \geq 4.14) = 0.01
\end{align*}\]
Una vez localizados los valores críticos de las dos tablas, se procede a
comparar dichos valores con la probabilidad de interés, la cual está
dada por \[\begin{align*}
\mathbb{P}(F_{8, 12} \geq 3)
\end{align*}\]
Entonces, como el valor crítico de interés se encuentra entre los
valores \(F_{0.05, 8, 14} = 2.70\) y \(F_{0.01, 8, 14} = 4.14\), se
tendrá que la probabilidad de interés estará entre el \(5\%\) y el
\(1\%\), tal que \[\begin{align*}
0.01 < \mathbb{P}(F_{8, 12} \geq 3) < 0.05
\end{align*}\]
En donde se evidencia que \[\begin{align*}
F_{0.05, 8, 14} = 2.70 \quad => \quad \mathbb{P}(F_{8, 14} \geq 2.70) = 0.05\\
F_{0.01, 8, 14} = 4.14 \quad => \quad \mathbb{P}(F_{8, 14} \geq 4.14) = 0.01
\end{align*}\]
Una vez localizados los valores críticos de las dos tablas, se procede a
comparar dichos valores con la probabilidad de interés, la cual está
dada por \[\begin{align*}
\mathbb{P}(F_{8, 12} \geq 3)
\end{align*}\]
Entonces, como el valor crítico de interés se encuentra entre los
valores \(F_{0.05, 8, 14} = 2.70\) y \(F_{0.01, 8, 14} = 4.14\), se
tendrá que la probabilidad de interés estará entre el \(5\%\) y el
\(1\%\), tal que \[\begin{align*}
0.01 < \mathbb{P}(F_{8, 12} \geq 3) < 0.05
\end{align*}\]
-
A diferencia del punto anterior, se observa que la probabilidad
propuesta en este caso es de la forma
\(\mathbb{P}(F_{10, 6} \leq 0.18)\), posee una estructura diferente a la
establecida por la tabla \(\mathbb{P}(F_{\nu_1, \nu_2}\geq f)\), por lo
cual, será necesario emplear el complemento de la probabilidad propuesta
para obtener una estructura similar a la que maneja la tabla, tal que
\[\begin{align*}
\mathbb{P}(F_{10, 6} \leq 0.18) = 1 - \mathbb{P}(F_{10, 6} > 0.18)
\end{align*}\]
Una vez empleado el complemento, podemos usar la probabilidad
\(\mathbb{P}(F_{10, 6} > 0.18)\) para calcular la probabilidad de
interés, mediante la búsqueda de la probabilidad, tal como se hizo en el
ejercicio anterior. Para ello, se debe localizar para las tablas
\(F_{0.05}\) y \(F_{0.01}\), los \(10\) grados de libertad del numerador
en la parte superior, mientras que, los \(6\) grados de libertad del
denominador en la parte izquierda de la tabla, y comparar los valores
encontrados del cruce de grados de libertad, con la probabilidad de
interés, tal como se ilustra acontinuación
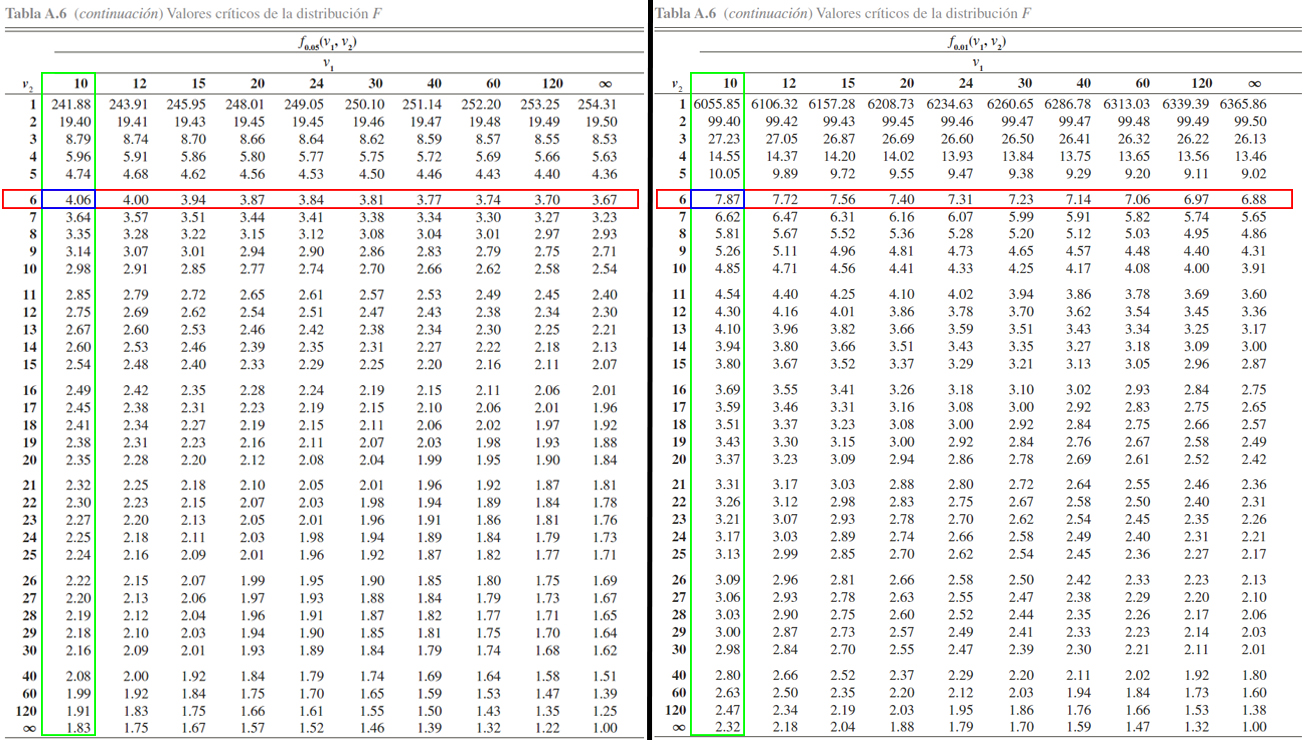 En donde se evidencia que \[\begin{align*}
F_{0.05, 10, 6} = 4.06 \quad => \quad \mathbb{P}(F_{10, 6} \geq 4.06) = 0.05\\
F_{0.01, 10, 6} = 7.87 \quad => \quad \mathbb{P}(F_{10, 6} \geq 7.87) = 0.01
\end{align*}\]
Entonces, como el valor crítico de interés se encuentra a la izquierda
de los valores \(F_{0.05, 10, 6} = 4.06\) y \(F_{0.01, 10, 6} = 7.87\),
se tendrá que la probabilidad de interés será mayor al \(5\%\) , tal que
\[\begin{align*}
\mathbb{P}(F_{10, 6} > 0.18) > 0.05
\end{align*}\]
y en consecuencia, se hace necesario realizar un paso adicional debido a
que el valor crítico se encuentra cercano a \(0\), el cuál consta en
aplicar el teorema de la cola izquierda para la distribución \(F\), con
el fin de calcular los valores críticos asociados a una \(F_{0.95}\) y
una \(F_{0.99}\), mediante la ecuación
\[\begin{align*}
F_{1-\alpha,v_1,v_2} = \frac{1}{F_{\alpha, v_2, v_1}}
\end{align*}\]
tal que, para calcular los valores críticos asociados a
\(F_{0.95, 10, 6}\) y \(F_{0.99, 10, 6}\), tendremos que
\[\begin{align*}
F_{0.95, 10, 6} = \frac{1}{F_{0.05, 6, 10}} \quad \quad \text{ y } \quad \quad F_{0.99, 10, 6} = \frac{1}{F_{0.01, 6, 10}}
\end{align*}\]
y por tanto, podremos calcular los valores críticos anteriores, mediante
el empleo de los valores críticos asociados a \(F_{0.05, 6, 10}\) y
\(F_{0.01, 6, 10}\), los cuales podemos calcular en las tablas de la
distribución \(F\) tal como se muestra acontinuación
En donde se evidencia que \[\begin{align*}
F_{0.05, 10, 6} = 4.06 \quad => \quad \mathbb{P}(F_{10, 6} \geq 4.06) = 0.05\\
F_{0.01, 10, 6} = 7.87 \quad => \quad \mathbb{P}(F_{10, 6} \geq 7.87) = 0.01
\end{align*}\]
Entonces, como el valor crítico de interés se encuentra a la izquierda
de los valores \(F_{0.05, 10, 6} = 4.06\) y \(F_{0.01, 10, 6} = 7.87\),
se tendrá que la probabilidad de interés será mayor al \(5\%\) , tal que
\[\begin{align*}
\mathbb{P}(F_{10, 6} > 0.18) > 0.05
\end{align*}\]
y en consecuencia, se hace necesario realizar un paso adicional debido a
que el valor crítico se encuentra cercano a \(0\), el cuál consta en
aplicar el teorema de la cola izquierda para la distribución \(F\), con
el fin de calcular los valores críticos asociados a una \(F_{0.95}\) y
una \(F_{0.99}\), mediante la ecuación
\[\begin{align*}
F_{1-\alpha,v_1,v_2} = \frac{1}{F_{\alpha, v_2, v_1}}
\end{align*}\]
tal que, para calcular los valores críticos asociados a
\(F_{0.95, 10, 6}\) y \(F_{0.99, 10, 6}\), tendremos que
\[\begin{align*}
F_{0.95, 10, 6} = \frac{1}{F_{0.05, 6, 10}} \quad \quad \text{ y } \quad \quad F_{0.99, 10, 6} = \frac{1}{F_{0.01, 6, 10}}
\end{align*}\]
y por tanto, podremos calcular los valores críticos anteriores, mediante
el empleo de los valores críticos asociados a \(F_{0.05, 6, 10}\) y
\(F_{0.01, 6, 10}\), los cuales podemos calcular en las tablas de la
distribución \(F\) tal como se muestra acontinuación
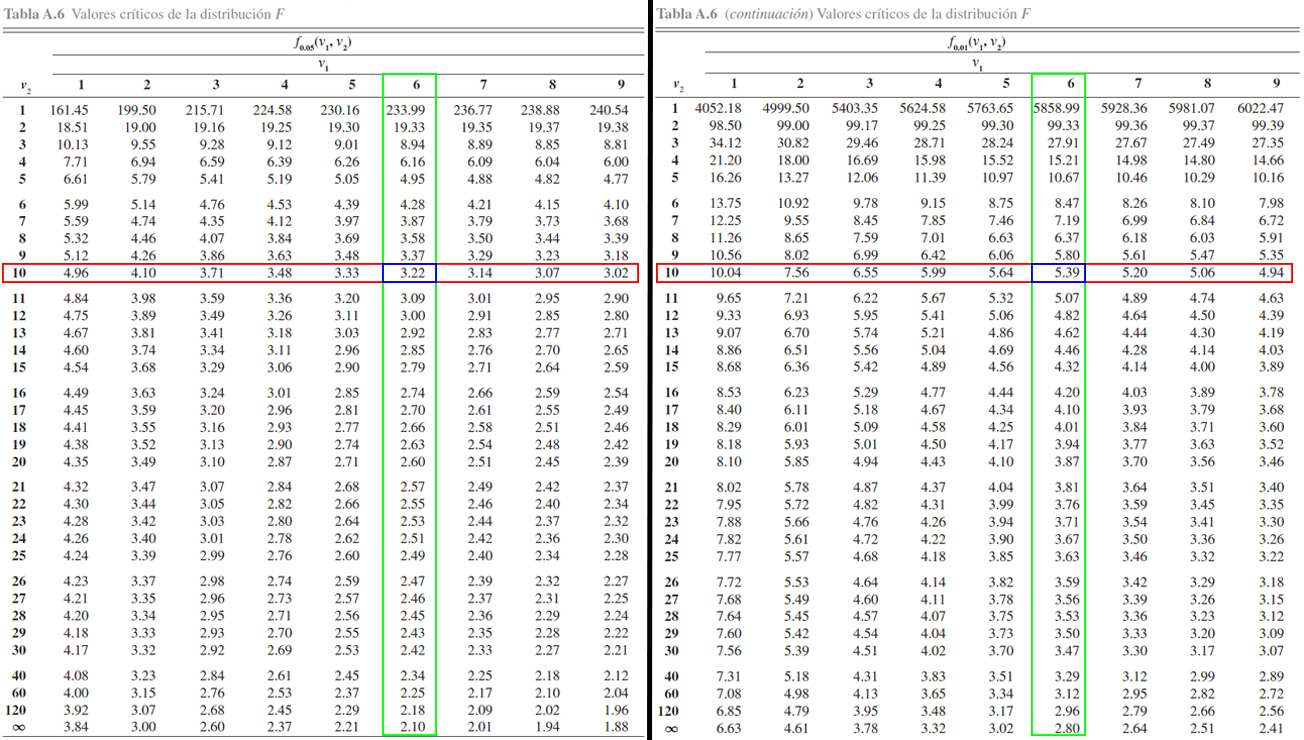 En donde se evidencia que \[\begin{align*}
F_{0.05, 6, 10} = 3.22 \quad => \quad \mathbb{P}(F_{6, 10} \geq 3.22) = 0.05\\
F_{0.01, 6, 10} = 5.39 \quad => \quad \mathbb{P}(F_{6, 10} \geq 5.39) = 0.01
\end{align*}\]
y por tanto, se tendrá que los valores para \(F_{0.95, 10, 6}\) y
\(F_{0.99, 10, 6}\) será respectivamente
\[\begin{align*}
F_{0.95, 10, 6} = \frac{1}{3.22} = 0.3105590 \quad => \quad \mathbb{P}(F_{10, 6} \geq 0.3105590) = 0.95\\
F_{0.99, 10, 6} = \frac{1}{5.39} = 0.1855288 \quad => \quad \mathbb{P}(F_{10, 6} \geq 0.1855288) = 0.99
\end{align*}\]
Ahora, basados en los \(4\) valores \(F\) calculados para \(10\) grados
de libertad para el numerador y \(6\) grados de libertad para el
denominador
\[\begin{align*}
F_{0.01, 10, 6} &= 7.87 \\
F_{0.05, 10, 6} &= 4.06 \\
F_{0.95, 10, 6} &= 0.3105590 \\
F_{0.99, 10, 6} &= 0.1855288
\end{align*}\]
tendremos que la probabilidad \(\mathbb{P}(F_{10, 6} > 0.18)\) es
aproximadamente de \(0.99\), es decir que
\[\begin{align*}
\mathbb{P}(F_{10, 6} > 0.18) \approx 0.99
\end{align*}\]
y por tanto, se tendrá que \[\begin{align*}
\mathbb{P}(F_{10, 6} \leq 0.18) &= 1 - \mathbb{P}(F_{10, 6} > 0.18) \\
&\approx 1 - 0.99 \\
&\approx 0.01
\end{align*}\]
En donde se evidencia que \[\begin{align*}
F_{0.05, 6, 10} = 3.22 \quad => \quad \mathbb{P}(F_{6, 10} \geq 3.22) = 0.05\\
F_{0.01, 6, 10} = 5.39 \quad => \quad \mathbb{P}(F_{6, 10} \geq 5.39) = 0.01
\end{align*}\]
y por tanto, se tendrá que los valores para \(F_{0.95, 10, 6}\) y
\(F_{0.99, 10, 6}\) será respectivamente
\[\begin{align*}
F_{0.95, 10, 6} = \frac{1}{3.22} = 0.3105590 \quad => \quad \mathbb{P}(F_{10, 6} \geq 0.3105590) = 0.95\\
F_{0.99, 10, 6} = \frac{1}{5.39} = 0.1855288 \quad => \quad \mathbb{P}(F_{10, 6} \geq 0.1855288) = 0.99
\end{align*}\]
Ahora, basados en los \(4\) valores \(F\) calculados para \(10\) grados
de libertad para el numerador y \(6\) grados de libertad para el
denominador
\[\begin{align*}
F_{0.01, 10, 6} &= 7.87 \\
F_{0.05, 10, 6} &= 4.06 \\
F_{0.95, 10, 6} &= 0.3105590 \\
F_{0.99, 10, 6} &= 0.1855288
\end{align*}\]
tendremos que la probabilidad \(\mathbb{P}(F_{10, 6} > 0.18)\) es
aproximadamente de \(0.99\), es decir que
\[\begin{align*}
\mathbb{P}(F_{10, 6} > 0.18) \approx 0.99
\end{align*}\]
y por tanto, se tendrá que \[\begin{align*}
\mathbb{P}(F_{10, 6} \leq 0.18) &= 1 - \mathbb{P}(F_{10, 6} > 0.18) \\
&\approx 1 - 0.99 \\
&\approx 0.01
\end{align*}\]
-
En este punto, nos piden calcular la
\(\mathbb{P}(0.31 < F_{15, 5} \leq 9.6)\), y se observa que la
estructura de dicha probabilidad es diferente a la establecida por la
tabla \(\mathbb{P}(F_{\nu_1, \nu_2}\geq f)\), Pero se aprecia que si
aplicamos las propiedades de la función de distribución acumulada para
el caso continuo, ya presentadas en la
Clase
08, y posteriormente calculamos el complemento de las
probabilidades, podemos llevar la probabilidad de interés a la forma
\[\begin{align*}
\mathbb{P}(0.31 < F_{15, 5} \leq 9.6) &= \mathbb{P}(F_{15, 5} \leq 9.6) - \mathbb{P}(F_{15, 5} \leq 0.31) \\
&= [1 - \mathbb{P}(F_{15, 5} > 9.6)] - [1- \mathbb{P}(F_{15, 5} > 0.31)] \\
&= \mathbb{P}(F_{15, 5} > 0.31) - \mathbb{P}(F_{15, 5} > 9.6)
\end{align*}\] obteniendo que la probabilidad
\(\mathbb{P}(0.31 < F_{15, 5} \leq 9.6)\), puede ser calculada mediante
el empleo de las probabilidades \(\mathbb{P}(F_{15, 5} > 0.31)\) y
\(\mathbb{P}(F_{15, 5} > 9.6)\). Para calcular esta probabilidad debemos
calcular los valores críticos \(F_{0.01, 15, 5}\), \(F_{0.05, 15, 5}\),
y los valores críticos, \(F_{0.05, 5, 15}\) y \(F_{0.01, 5, 15}\), los
cuales se usan para calcular \(F_{0.95, 15, 5}\) y \(F_{0.99, 15, 5}\).
A continuación se ilusta la localización de los \(4\) valores de interés
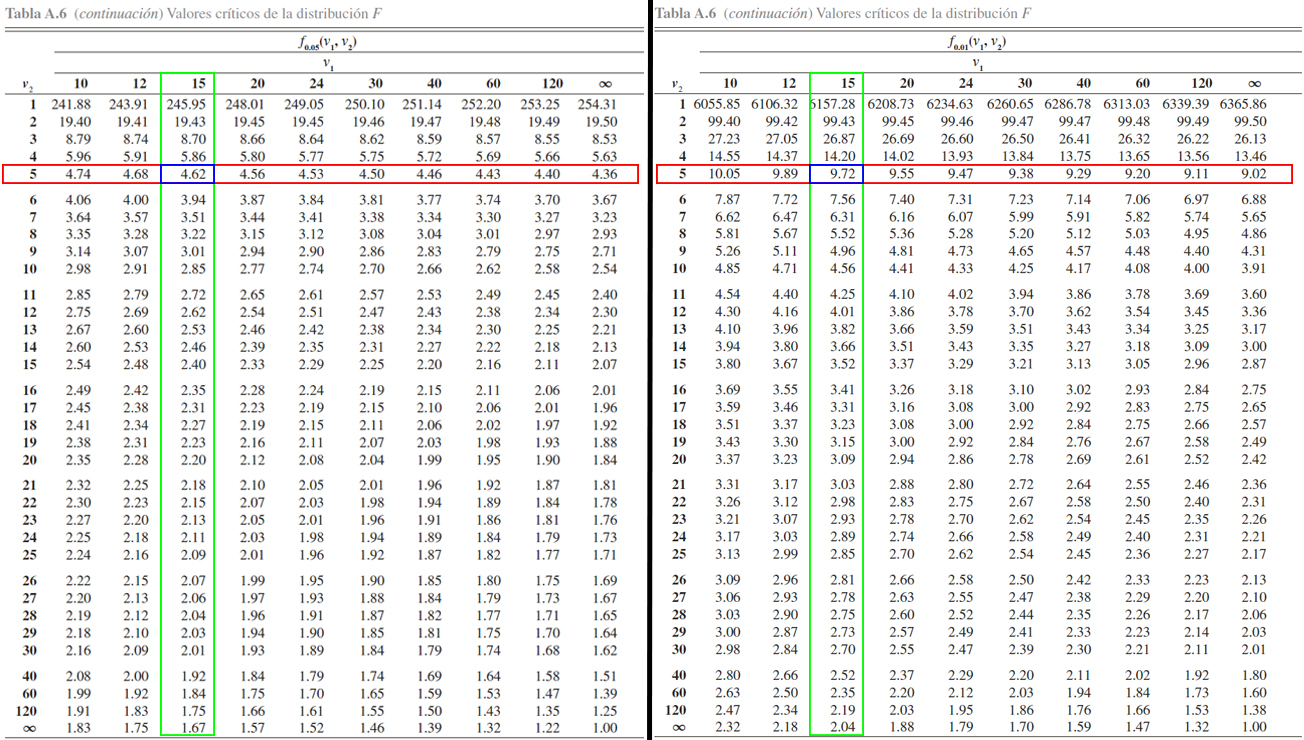
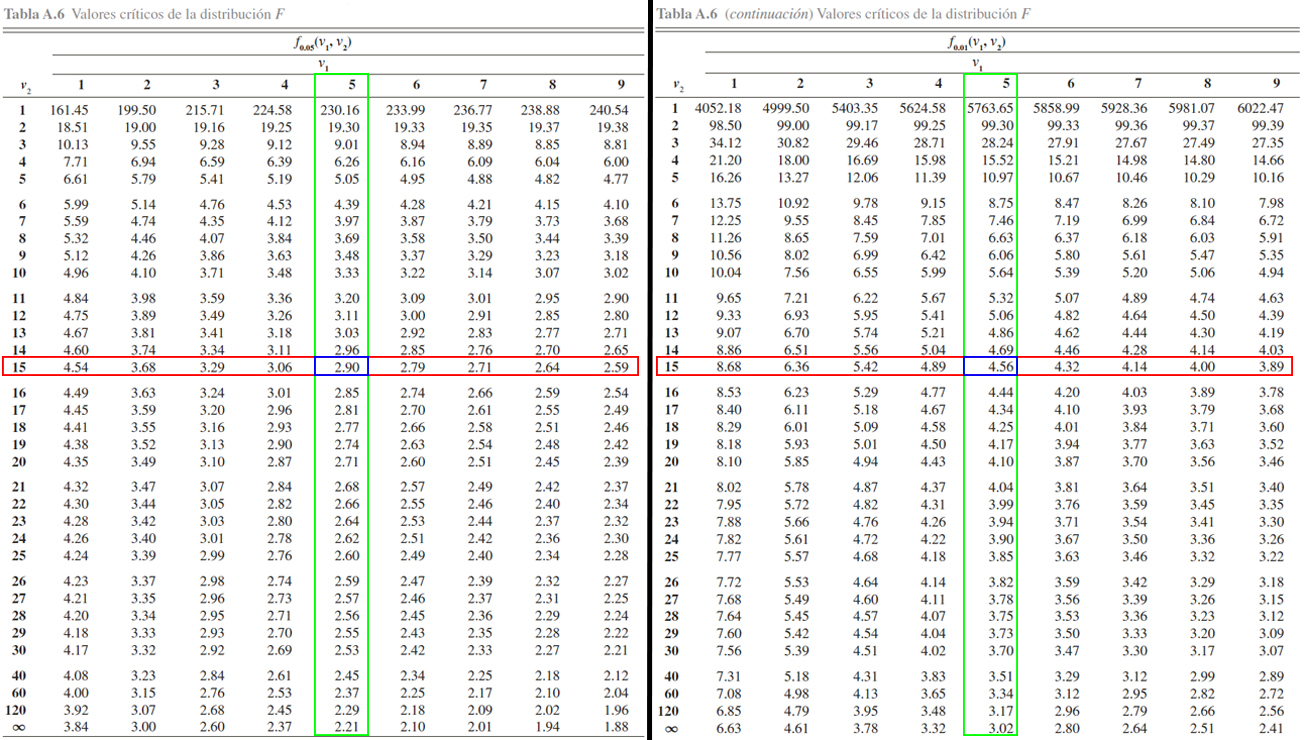 Donde se aprecia que \[\begin{align*}
F_{0.01, 15, 5} &= 9.72 \\
F_{0.05, 15, 5} &= 4.62 \\
F_{0.95, 15, 5} &= \frac{1}{F_{0.05, 5, 15}} = \frac{1}{2.90} = 0.3448276 \\
F_{0.99, 15, 5} &= \frac{1}{F_{0.01, 5, 15}} = \frac{1}{4.56} = 0.2192982
\end{align*}\]
Una vez localizados los \(4\) valores críticos, se procede a comparar
dichos valores con las probabilidad de interés, las cuales están dadas
por \[\begin{align*}
\mathbb{P}(F_{15, 5} > 0.31) \quad \text{ y } \quad \mathbb{P}(F_{15, 5} > 9.6)
\end{align*}\]
En el caso del valor crítico \(0.31\), se observa que éste se encuentra
entre los valores \(F_{0.99, 15, 5} = 0.2192982\) y
\(F_{0.95, 15, 5} = 0.3448276\), siendo el valor más cercano
\(F_{0.95, 15, 5}\), y en consecuencia diremos que \[\begin{align*}
\mathbb{P}(F_{15, 5} > 0.31) \approx 0.95
\end{align*}\]
mientras que, para el caso del valor crítico \(9.6\), se observa que se
encuentra entre \(F_{0.05, 15, 5} = 4.62\) y \(F_{0.01, 15, 5} = 9.72\),
siendo el valor más cercano \(F_{0.01, 15, 5} = 9.72\), y en
consecuencia diremos \[\begin{align*}
\mathbb{P}(F_{15, 5} > 9.6) \approx 0.01
\end{align*}\]
Y por tanto se tendrá que \[\begin{align*}
\mathbb{P}(0.31 < F_{15, 5} \leq 9.6) &= \mathbb{P}(F_{15, 5} > 0.31) - \mathbb{P}(F_{15, 5} > 9.6)\\
&\approx 0.95 - 0.01\\
&\approx 0.94
\end{align*}\]
Donde se aprecia que \[\begin{align*}
F_{0.01, 15, 5} &= 9.72 \\
F_{0.05, 15, 5} &= 4.62 \\
F_{0.95, 15, 5} &= \frac{1}{F_{0.05, 5, 15}} = \frac{1}{2.90} = 0.3448276 \\
F_{0.99, 15, 5} &= \frac{1}{F_{0.01, 5, 15}} = \frac{1}{4.56} = 0.2192982
\end{align*}\]
Una vez localizados los \(4\) valores críticos, se procede a comparar
dichos valores con las probabilidad de interés, las cuales están dadas
por \[\begin{align*}
\mathbb{P}(F_{15, 5} > 0.31) \quad \text{ y } \quad \mathbb{P}(F_{15, 5} > 9.6)
\end{align*}\]
En el caso del valor crítico \(0.31\), se observa que éste se encuentra
entre los valores \(F_{0.99, 15, 5} = 0.2192982\) y
\(F_{0.95, 15, 5} = 0.3448276\), siendo el valor más cercano
\(F_{0.95, 15, 5}\), y en consecuencia diremos que \[\begin{align*}
\mathbb{P}(F_{15, 5} > 0.31) \approx 0.95
\end{align*}\]
mientras que, para el caso del valor crítico \(9.6\), se observa que se
encuentra entre \(F_{0.05, 15, 5} = 4.62\) y \(F_{0.01, 15, 5} = 9.72\),
siendo el valor más cercano \(F_{0.01, 15, 5} = 9.72\), y en
consecuencia diremos \[\begin{align*}
\mathbb{P}(F_{15, 5} > 9.6) \approx 0.01
\end{align*}\]
Y por tanto se tendrá que \[\begin{align*}
\mathbb{P}(0.31 < F_{15, 5} \leq 9.6) &= \mathbb{P}(F_{15, 5} > 0.31) - \mathbb{P}(F_{15, 5} > 9.6)\\
&\approx 0.95 - 0.01\\
&\approx 0.94
\end{align*}\]
-
En este punto, a diferencia de los puntos anteriores, nos están dando el
valor de la probabilidad, junto a los grados de libertad del numerador y
el denominador, y nos piden encontrar el valor crítico \(f\) asociado a
dichos valores, tal que \[\begin{align*}
\mathbb{P}(F_{12, 12} \geq f) = 0.05
\end{align*}\]
Donde evidenciamos que la probabilidad de interés ya posee la estructura
de la tabla \(\mathbb{P}(F_{\nu_1, \nu_2}\geq f)\), y por tanto, podemos
encontrar el valor crítico de forma directa en la tabla, buscando en la
parte superior los grados de libertad \(\nu_1=12\) y en la parte
izquierda, los grados de libertad \(\nu_2=12\) en la tabla \(F_{0.05}\),
para encontrar el valor crítico en donde se cruzan los grados de
libertad, tal como se ilustra a continuación
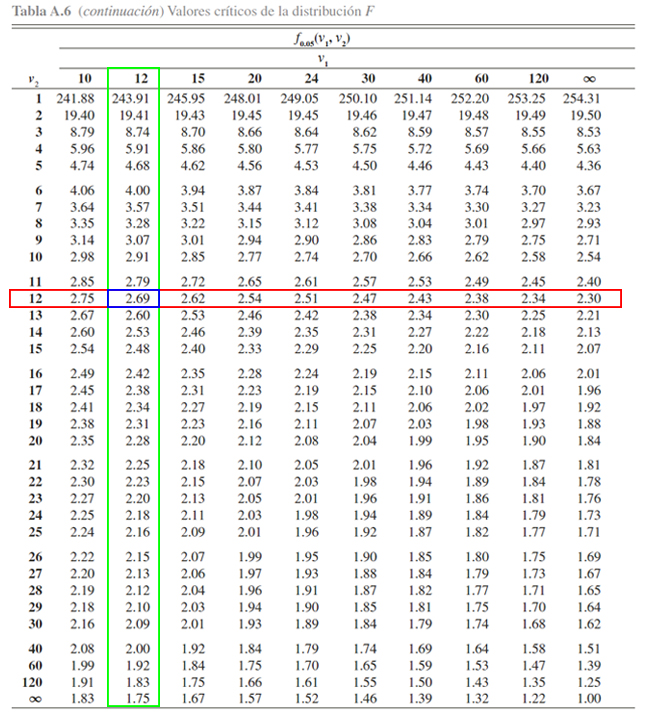 En donde se evidencia, que el valor crítico \(f\) asociado a una
probabilidad de \(0.05\) y a \(12\) grados de libertad en el numerador
junto a \(12\) grados de libertad en el denominador, es igual a
\(2.69\), es decir
\[\begin{align*}
\mathbb{P}(F_{12, 12} \geq 2.69) = 0.05
\end{align*}\]
En donde se evidencia, que el valor crítico \(f\) asociado a una
probabilidad de \(0.05\) y a \(12\) grados de libertad en el numerador
junto a \(12\) grados de libertad en el denominador, es igual a
\(2.69\), es decir
\[\begin{align*}
\mathbb{P}(F_{12, 12} \geq 2.69) = 0.05
\end{align*}\]
Ejercicio
Se aplican pruebas a \(10\) cables conductores soldados a un dispositivo semiconductor con el fin de determinar su resistencia a la tracción. Las pruebas demostraron que para romper la union se requiere las libras de fuerza que se listan a continuación.
| Sin Encapsulado | 19.8 | 12.7 | 13.2 | 16.9 | 10.6 | 18.8 | 11.1 | 14.3 | 17.0 | 12.5 |
Otra conjunto de \(8\) cables conductores que forman otro dispositivo, se encapsulan y se prueban para determinar si el encapsulado aumenta la resistencia a la tracción, obteniendo para este caso se requirieron las siguientes libras de fuerza para romper la unión
| Con Encapsulado | 24.9 | 22.9 | 23.6 | 22.1 | 20.3 | 21.6 | 21.9 | 22.5 |
Cuál es la probabilidad de que la variabilidad de los cables sin encapsulado sea mayor a la variabilidad de los cables con encapsulado?
Solución
En este punto, nos preguntan sobre la probabilidad de que la varianza de los cables sin encapsulado, \(\sigma^2_S\), sea mayor a la varianza de los cables con encapsulado, \(\sigma^2_C\), esto es \[\begin{align*} \mathbb{P}(\sigma^2_S > \sigma^2_C) = \mathbb{P}\left(\frac{\sigma^2_S}{\sigma^2_C} > 1\right) \end{align*}\] Es de anotar que, al no conocer la distribución de probabilidad del cocience de las varianzas, debemos realizar operaciones matemáticas para llevar la probabilidad planteada a una forma conocida, tal como lo es la estructura de una distribución \(F\) con \(n_C-1\) grados de libertad en el numerador y \(n_S-1\) grados de libertad en el denominador, tal que \[\begin{align*} F_c = \frac{S^2_C\sigma^2_S}{S^2_S\sigma^2_C} \sim F_{n_C-1, n_S-1} \end{align*}\] En donde apreciamos que requerimos de las varianzas muestrales \(S^2_C\) y \(S^2_S\), los cuales podemos calcular a partir de los datos muestrales y los tamaños de muestra \(n_C=8\) y \(n_S=10\), tal que al realizar el cálculo obtenemos \[\begin{align*} S^2_C = 1.899286 \quad \text{ y } \quad S^2_S = 10.441 \end{align*}\] y con estos valores podemos hacer las operaciones matemáticas correspondientes para llevar la probabilidad de interés a la estructura deseada, tal que \[\begin{align*} \mathbb{P}(\sigma^2_S > \sigma^2_C) &= \mathbb{P}\left(\frac{\sigma^2_S}{\sigma^2_C} > 1\right) \\ &= \mathbb{P}\left(\frac{S^2_C\sigma^2_S}{S^2_S\sigma^2_C} > \frac{1.899286}{10.441}(1)\right) \\ &= \mathbb{P}\left(F_{8-1, 10-1} > 0.1819065\right) \end{align*}\] entonces podemos encontrar la probabilidad de interés de forma aproximada, empleando la Tabla de la Distribución F de Fisher-Snedecor, o la probabilidad exacta empleando la función pf() del software R o las funciones DISTR.F.N() o DISTR.F.CD() de Excel, tal que \[\begin{align*} \mathbb{P}\left(F_{7, 9} > 0.1819065\right) = 0.9824406 \end{align*}\] lo cual, dada la equivalencia de la igualdad anterior, significará que \[\begin{align*} \mathbb{P}(\sigma^2_S > \sigma^2_C) = 0.9824406 \end{align*}\] por tanto, se tiene una probabilidad del \(98.24\%\) de que la variabilidad de los cables sin encapsulado sea mayor a la variabilidad de los cables con encapsulado, es decir, que es muy probable que el encapsulado disminuya la variabilidad de la resistencia a la tracción.
Distribución muestral para una proporción $p$
Sea $X_1, X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$, tal que $X\sim b(n,p)$. Entonces si $n$ es suficientemente
grande, y la proporción $p$ no está muy cercana a $0$ o a $1$, tal
que $np$ y $n(1-p)>5$, entonces se puede probar que
\begin{align*} \hat{p} = \frac{x}{n} \stackrel{a}{\sim} N\left(p, \frac{p(1-p)}{n}\right) \end{align*}
donde por teorema de estandarización se obtendrá que
\begin{align*} Z_c = \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}} \stackrel{a}{\sim} N(0,1) \end{align*}
Ejercicio
Suponga que se realiza un estudio sobre el salario de los estudiantes de ingeniería industrial una vez finalizan su pregrado y se incertan en el mercado laboral. Para ello, se le pregunta a \(15\) egresados seleccionados de forma aleatoria y se les pregunta cuál es el salario que devengan actualmente, obteniendo los siguientes resultados en millones de pesos \[\begin{align*} 1.78 \quad 2.93 \quad 1.22 \quad 1.27 \quad 1.17 \\ 1.03 \quad 1.24 \quad 2.07 \quad 2.04 \quad 1.28 \\ 1.53 \quad 0.98 \quad 1.73 \quad 1.38 \quad 3.24 \end{align*}\] Basados en la información anterior, calcule la probabilidad de que la proporción de egresados que tienen un salario superior a \(2\) millones de pesos sea mayor al \(40\%\).
Solución
En este punto, nos preguntan por la proporción de egresados que tienen un salario superior a \(2\) millones de pesos sea mayor al \(40\%\), es decir \[\begin{align*} \mathbb{P}(p > 0.4) \end{align*}\] Pero al observar la información recolectada por los \(15\) egresados, apreciamos que que nos dan el salario que devengan, y no la proporción muestral, de quienes tienen un salario superior a \(2\) millones de pesos, por lo cual, será necesario calcular la proporción muestral, y para ello, denotaremos como \(1\) aquellas observaciones que sean superiores a \(2\) millones de pesos, y \(0\) aquellas observaciones que no cumplan la condición, tal que \[\begin{align*} \underset{0}{1.78} \quad \underset{1}{2.93} \quad \underset{0}{1.22} \quad \underset{0}{1.27} \quad \underset{0}{1.17} \\ \underset{0}{1.03} \quad \underset{0}{1.24} \quad \underset{1}{2.07} \quad \underset{1}{2.04} \quad \underset{0}{1.28} \\ \underset{0}{1.53} \quad \underset{0}{0.98} \quad \underset{0}{1.73} \quad \underset{0}{1.38} \quad \underset{1}{3.24} \end{align*}\] Entonces, si los \(1\) representa los éxitos, tendremos un total de \(x=4\) éxitos en las \(n=15\) muestras, entonces podemos aplicar la fórmula de frecuencia relativa para calcular la proporción muestral de egresados que poseen salarios superiores a \(2\) millones. \[\begin{align*} \hat{p} &= \frac{\text{# éxitos}}{\text{Total ensayos}} \\ &= \frac{x}{n} \\ &= \frac{4}{15} \\ &= 0.2666667 \end{align*}\] Una vez calculada la proporción muestral, podemos emplear ésta para calcular la probabilidad de interés, mediante el empleo de operaciones matemáticas, de tal forma que la probabilidad planteada tenga la estructura de una distribución de probabilidad conocida, lo cual, en este caso, será una distribución aproximadamente normal, tal que \[\begin{align*} Z_c = \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}} \stackrel{a}{\sim} N(0,1) \end{align*}\] Con esta estructura en mente, se procede a realizar la operaciones correspondientes para llevar la probabilidad original, a la forma conocida, tal que \[\begin{align*} \mathbb{P}(p > 0.4) &= \mathbb{P}(- p < - 0.4) \\ &= \mathbb{P}(\hat{p}- p < 0.2666667 - 0.4) \\ &= \mathbb{P}\left(\frac{\hat{p}- p}{\sqrt{\frac{p(1-p)}{n}}} < \frac{0.2666667 - 0.4}{\sqrt{\frac{0.4(1-0.4)}{15}}}\right) \\ &= \mathbb{P}\left(Z < -1.054092\right) \end{align*}\] Y como \(Z \sim N(0,1)\), entonces podemos encontrar la probabilidad de interés, empleando la Tabla de la Distribución Normal Estándar, la función pnorm() del software R o la función DISTR.NORM.ESTAND.N() de Excel, tal que \[\begin{align*} \mathbb{P}(Z < -1.054092) = 0.1459204 \end{align*}\] lo cual, dada la equivalencia de la igualdad anterior, significará que \[\begin{align*} \mathbb{P}(p > 0.4) = 0.1459204 \end{align*}\] Y por tanto, se tendrá un \(14.59\%\) de probabilidad de que la proporción de egresados que tienen un salario superior a \(2\) millones de pesos, sea mayor al \(40\%\).