Probabilidad Condicional
Es la probabilidad de que ocurra un evento $A$, cuando se sabe que ya
ocurrió un evento $B$, se denota por $\mathbb P(A|B)$ y se define
como
\begin{align*} \mathbb P(A|B)=\frac{\mathbb P(A\cap B)}{\mathbb P(B)}; \text{ con } \mathbb P(B)>0 \end{align*}
Ejercicio
Suponga que se realiza un estudio en la Facultad de Ciencias Económicas, en donde se le pregunta a sus estudiantes, en cuál deporte preferirían practicar entre Fútbol, Baloncesto, Voleibol y Tenis. Dicha pregunta se le realiza a un total de \(400\) estudiantes, encontrando los siguientes resultados
| Fútbol | Baloncesto | Voleibol | Tenis | |
|---|---|---|---|---|
| Administración de empresas | 48 | 27 | 22 | 23 |
| Contaduría | 34 | 41 | 25 | 10 |
| Economía | 66 | 51 | 13 | 40 |
A partir de la tabla anterior
- Construya una tabla de probabilidades.
- ¿Cuál es la probabilidad de que se seleccione un estudiante que prefiera el Fútbol sobre los otros deportes?
- ¿Cuál es la probabilidad de que se seleccione un estudiante que estudie Contaduría?
- ¿Cuál es la probabilidad de que se seleccione un estudiante que estudie Economía y prefiera el Tenis sobre los demás deportes?
- Si se selecciona un estudiante de Contaduría, ¿Cuál es la probabilidad de que prefiera el Voleibol sobre los otros deportes?
- ¿Cual es la probabilidad de que un estudiante sea de Economía, si se sabe que prefiere el Baloncesto sobre los otros deportes?
Solución
-
Dado que el interés es construir una tabla de probabilidades, es
cuestión de dividir cada una de las entradas por el total de estudiantes
encuestados, esto con el fin de que la suma de todos los puntos
muestrales sea igual a \(1\), es decir, \(\mathbb{P}(S) = 1\), siendo
\(S\) el espacio muestral. Por tanto se tendrá que
Fútbol Baloncesto Voleibol Tenis Administración de empresas 0.120 0.0675 0.0550 0.0575 Contaduría 0.085 0.1025 0.0625 0.0250 Economía 0.165 0.1275 0.0325 0.1000 -
Dado que nos interesa solo la probabilidad de que al estudiante
seleccionado prefiera el Fútbol, entonces podemos calcular dicha
probabilidad mediante el cálculo de la suma marginal de la columna de
Fútbol, dicha suma se conoce como
Probabilidad
total, de la cual se hablará más adelante.
\[\begin{align*} \mathbb{P}(F)=0.120+0.085+0.165=0.37 \end{align*}\] Por tanto, se tendrá un \(37\%\) de probabilidad de que el estudiante seleccionado prefiera el Fútbol sobre los demás deportes.Fútbol Baloncesto Voleibol Tenis Administración de empresas 0.120 0.0675 0.0550 0.0575 Contaduría 0.085 0.1025 0.0625 0.0250 Economía 0.165 0.1275 0.0325 0.1000 -
Similar al punto anterior, dado que solo nos interesa la probabilidad de
que el estudiante sea de Contaduría, entonces será posible realizar el
cálculo mediante la suma marginal de la fila de Contaduría, donde dicha
suma se conoce como
Probabilidad
total, de la cual se hablará más adelante.
\[\begin{align*} \mathbb{P}(C)=0.085+0.1025+0.0625+0.0250=0.275 \end{align*}\] Por tanto, se tendrá un \(27.5\%\) de probabilidad de que el estudiante seleccionado sea de Contaduría.Fútbol Baloncesto Voleibol Tenis Administración de empresas 0.120 0.0675 0.0550 0.0575 Contaduría 0.085 0.1025 0.0625 0.0250 Economía 0.165 0.1275 0.0325 0.1000 -
Como el interés se centra en la probabilidad de que un estudiante curse
la carrera de Economía y prefiera el Tenis sobre los
demás deportes, debemos localizar el lugar en donde se cruza la columna
de Tenis y la fila de Economía.
De donde obtendremos que \[\begin{align*} \mathbb{P}(E \cap V)=0.10 \end{align*}\] lo cual indica que la probabilidad de que un estudiante sea de Economía y prefiera el Tenis sobre los otros deportes es del \(10\%\).Fútbol Baloncesto Voleibol Tenis Administración de empresas 0.120 0.0675 0.0550 0.0575 Contaduría 0.085 0.1025 0.0625 0.0250 Economía 0.165 0.1275 0.0325 0.1000 -
En este punto, nos dicen que ya se sabe que el estudiante realiza sus
estudios en Contaduría, lo cual es un condicional a la hora de realizar
el cálculo de la probabilidad de interés. Entonces, como nos piden
encontrar la probabilidad de que prefiera Voleibol, dado
que se sabe que estudia Contaduría, entonces tendremos que
realizar el cálculo de \[\begin{align*}
\mathbb{P}(V|C) = \frac{\mathbb{P}(V \cap C)}{\mathbb{P}(C)}
\end{align*}\]
Tendremos entonces que la \(\mathbb{P}(C) = 0.275\) obtenida a partir de
la suma de las probabilidades individuales en la fila de Contaduría,
mientras que la \(\mathbb{P}(V \cap C) = 0.0625\), obtenida a partir de
la casilla en donde se intersectan la columna de Voleibol y fila de
Contaduría.
Y por tanto se tendrá que \[\begin{align*} \mathbb{P}(V|C) = \frac{0.0625}{0.275} = 0.2273 \end{align*}\] Lo cual indica que la probabilidad de que se seleccione un estudiante que prefiera Voleibol, dado que se sabe que estudia Contaduría, es del \(22.73\%\). -
Similar al punto anterior, solo que en este caso se desea calcular la
probabilidad de que un estudiante seleccionado estudie Economía,
dado que se sabe que prefiere el Baloncesto sobre los
otros deportes, es decir,
\[\begin{align*}
\mathbb{P}(E|B) = \frac{\mathbb{P}(E \cap B)}{\mathbb{P}(B)}
\end{align*}\] De esto tendremos que \(\mathbb{P}(B) = 0.2975\) obtenida
a partir de la suma de las probabilidades individuales en la columna de
Baloncesto, mientras que la \(\mathbb{P}(E \cap B) = 0.1275\), obtenida
a partir de la casilla en donde se intersectan la fila de Economía y la
columna de Baloncesto.
Lo cual dará como resultado que \[\begin{align*} \mathbb{P}(E|B) = \frac{0.1275}{0.2975} = 0.4286 \end{align*}\] Lo cual indica que la probabilidad de que se seleccione un estudiante que curse Economía, dado que se sabe que prefiere el Baloncesto sobre otros deportes, es del \(42.86\%\).
Regla multiplicativa
Si un experimento estadístico pueden ocurrir dos eventos $A$ y $B$,
entonces
\begin{align*} \mathbb P(A\cap B)=\mathbb P(B)\mathbb P(A|B)=\mathbb P(A)\mathbb P(B|A); \text{ para } \mathbb P(B)>0 \text{ y } \mathbb P(A)>0 \end{align*}
En general, si pueden ocurrir los eventos $A_1, A_2, \ldots, A_n$,
entonces
\begin{align*} \mathbb P\left(\underset{i=1}{\stackrel{n}{\cap}} A_i\right)=\mathbb P(A_1) \mathbb P(A_2|A_1)\mathbb P(A_3|A_1\cap A_2)\ldots \mathbb P\left(A_n \Big|\underset{i=1}{\stackrel{n-1}{\cap}} A_i\right) \end{align*}
Ejercicio
Una bolsa contiene seis pelotas rojas y cuatro azules, una segunda contiene siete rojas y dos azules. El experimento consiste en seleccionar una pelota al azar de la primera bolsa y colocarla dentro de la segunda bolsa. Seguidamente se selecciona una de la segunda bolsa y se coloca en la primera bolsa.
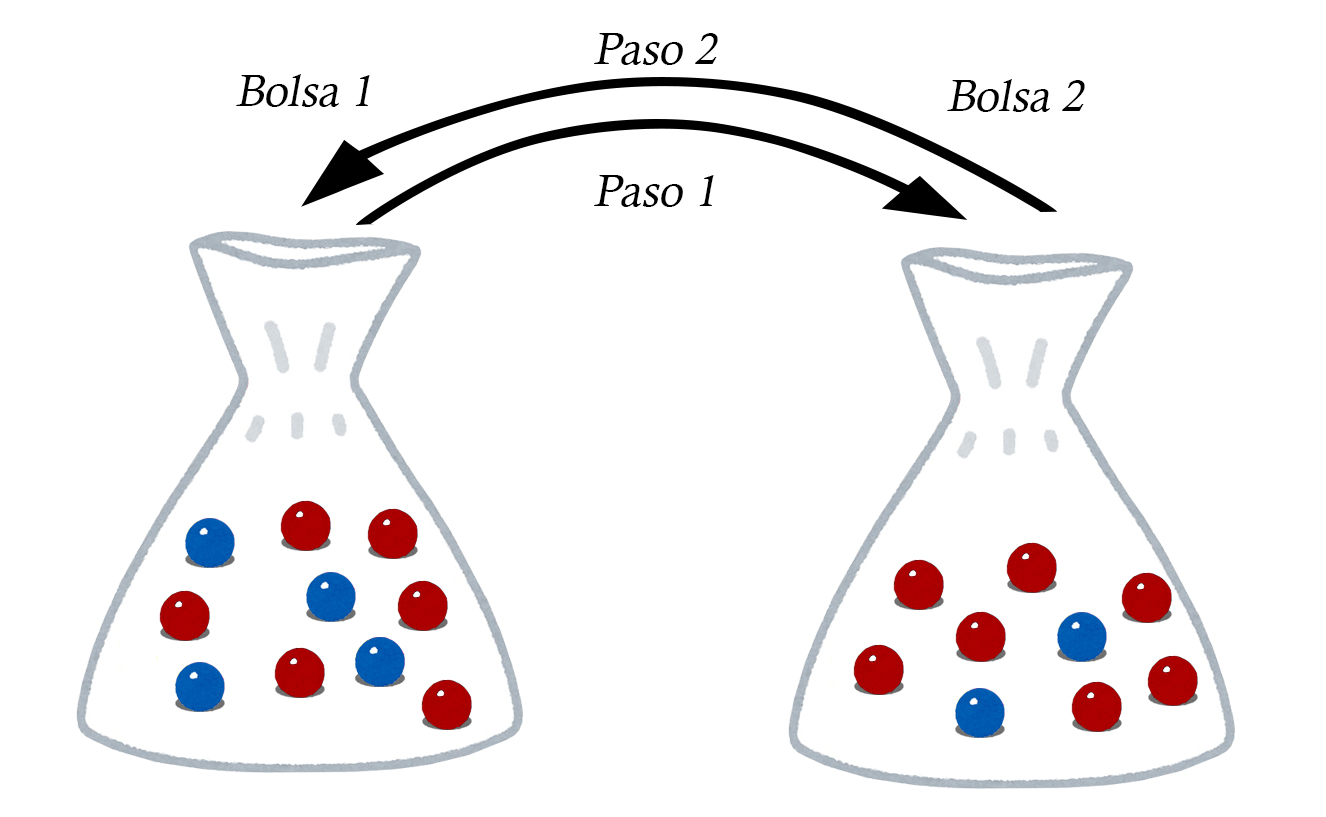
- Cuál es la probabilidad de que se seleccione una pelota roja de la primera bolsa y una roja de la segunda bolsa?
- Al final del proceso de selección, Cuál es la probabilidad de que el números de pelotas rojas y azules que hay en la primera bolsa sean idénticos a los iniciales?
Solución
-
Para resolver tal problema podemos emplear lo conocido como un
Diagrama de Árbol el cual consta de gráficas todos los
posibles resultados, de la siguiente forma
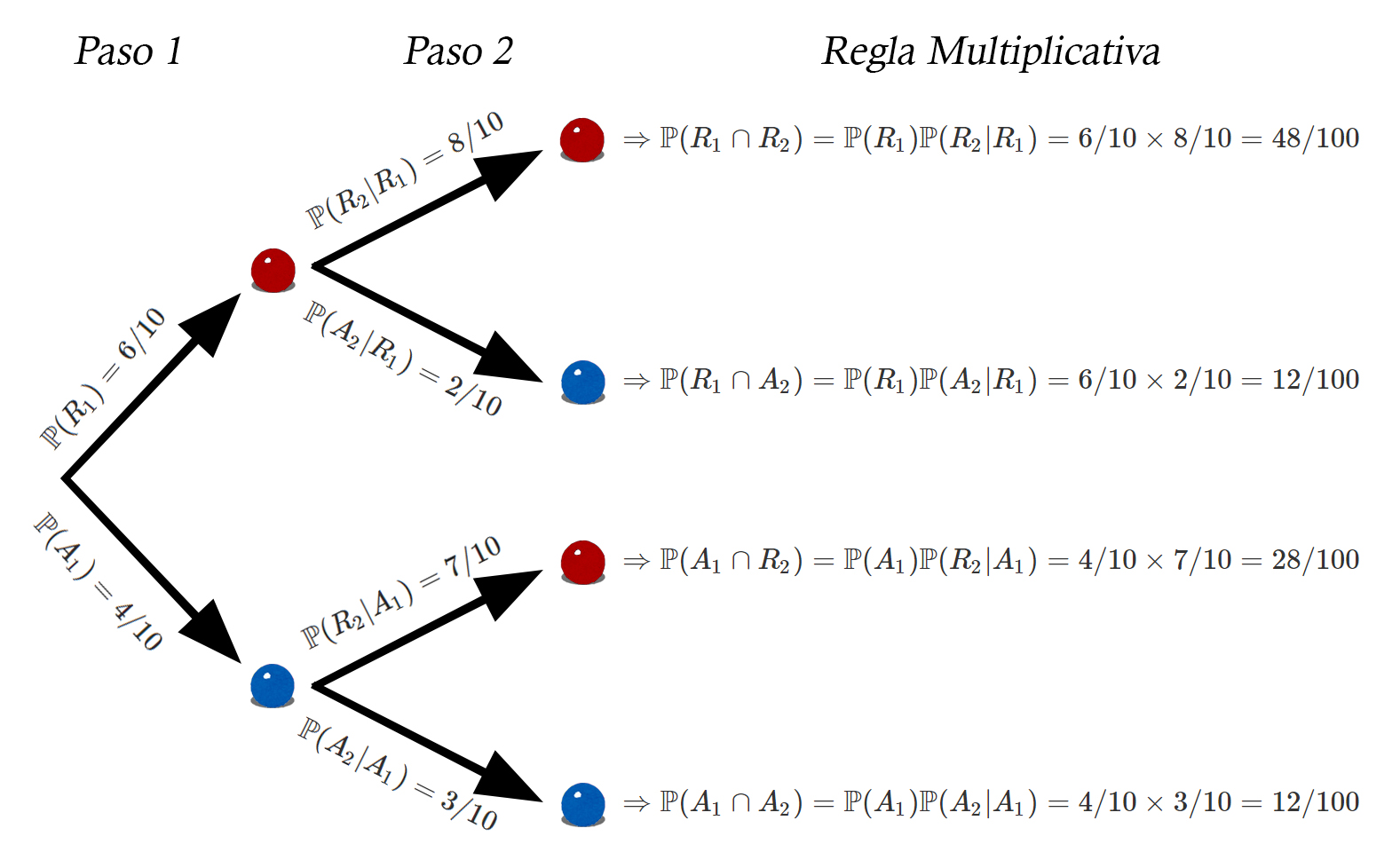
Entonces, si observamos el diagrama de árbol, podemos apreciar que la probabilidad de que se saque una bola roja de la primera bolsa (primer paso) es de \[\begin{align*} \mathbb{P}(R_1) = \frac{6}{10} \end{align*}\] mientras que la probabilidad de sacar una bola roja de la segunda bolsa (segundo paso) es de \[\begin{align*} \mathbb{P}(R_2|R_1) = \frac{8}{10} \end{align*}\] Y por tanto, al aplicar la regla multiplicativa, tenemos que la probabilidad de sacar una bola roja de la primera bolsa, introducirla en la segunda bolsa, y posteriormente sacar una bola roja de la segunda bolsa, es de \[\begin{align*} \mathbb{P}(R_1 \cap R_2) =\mathbb{P}(R_1) \mathbb{P}(R_2|R_1) = \frac{6}{10} \times \frac{8}{10} = \frac{48}{100} \end{align*}\] -
Para saber cuál es la probabilidad de que el números de pelotas rojas y
azules que hay en la primera bolsa sean idénticos a los iniciales, luego
de realizar los dos pasos, es necesario evaluar nuevamente el diagrama
de árbol para ver en qué ramas del gráfico se cumple la condición final.
Entonces, para cumplir la condición se aprecia que sería necesario cumplir dos posibles situaciones. La primera situación, sería cuando se saca una bola roja de la primera bolsa (primer paso) y luego una bola roja de la segunda bolsa (segundo paso), lo cual daría como resultado \[\begin{align*} \mathbb{P}(R_1 \cap R_2) =\mathbb{P}(R_1) \mathbb{P}(R_2|R_1) = \frac{6}{10} \times \frac{8}{10} = \frac{48}{100} \end{align*}\] mientras que la segunda situación, sería cuando se saca una bola azul de la primera bolsa (primer paso) y luego una bola azul de la segunda bolsa (segundo paso), lo cual daría como resultado \[\begin{align*} \mathbb{P}(A_1 \cap A_2) =\mathbb{P}(A_1) \mathbb{P}(A_2|A_1) = \frac{4}{10} \times \frac{3}{10} = \frac{12}{100} \end{align*}\] Y por tanto, la probabilidad de que el números de pelotas rojas y azules que hay en la primera bolsa sean idénticos a los iniciales, estará dado por \[\begin{align*} \mathbb{P}(R_1 \cap R_2) + \mathbb{P}(A_1 \cap A_2) = \frac{48}{100} + \frac{12}{100} = \frac{60}{100} \end{align*}\]
Independencia entre eventos
Si un experimento estadístico pueden ocurrir dos eventos $A$ y $B$
que son independientes entre si, entonces
\begin{align*} \mathbb P(A|B)=\mathbb P(A) \quad \text{ o } \quad \mathbb P(B|A)=\mathbb P(B) \end{align*}
lo cual es equivalente a
\begin{align*} \mathbb P(A\cap B)=\mathbb P(A)\mathbb P(B) \end{align*}
En cualquier otro caso, los eventos $A$ y $B$ son dependientes.
Ejercicio
Una bolsa contiene \(100\) pelotas, de las cuales \(25\) son rojas, \(40\) son azules y \(35\) son negras.
- Si se seleccionan dos pelotas, ¿Cuál es la probabilidad de que la primera sea negra y la segunda sea azul, si la primera pelota se reemplaza antes de sacar la segunda? Las probabilidades son independientes?
- Si se seleccionan tres pelotas, ¿Cuál es la probabilidad de que la primera sea azul, la segunda sea negra y la tercera sea roja, si la primera pelota se reemplaza antes de sacar la segunda, pero no se realiza ningún reemplazo en la segunda antes de sacar la tercera? Las probabilidades son independientes?
Solución
-
Dado que la selección de las pelotas se realiza con reemplazo, tendremos
que la probabilidad de un paso a otro permanecerá constante entre todas
las pelotas, por ejemplo, si se saca una bola negra en el primer paso,
entonces se registrará su color, se volverá a introducir en la bolsa, y
posteriormente se realizará el segundo paso, asegurando que la
probabilidad que tendrán todas las bolas de ser seleccionadas permanezca
invariable, respecto a las probabilidades iniciales.
Dado lo anterior tendremos el siguiente escenario
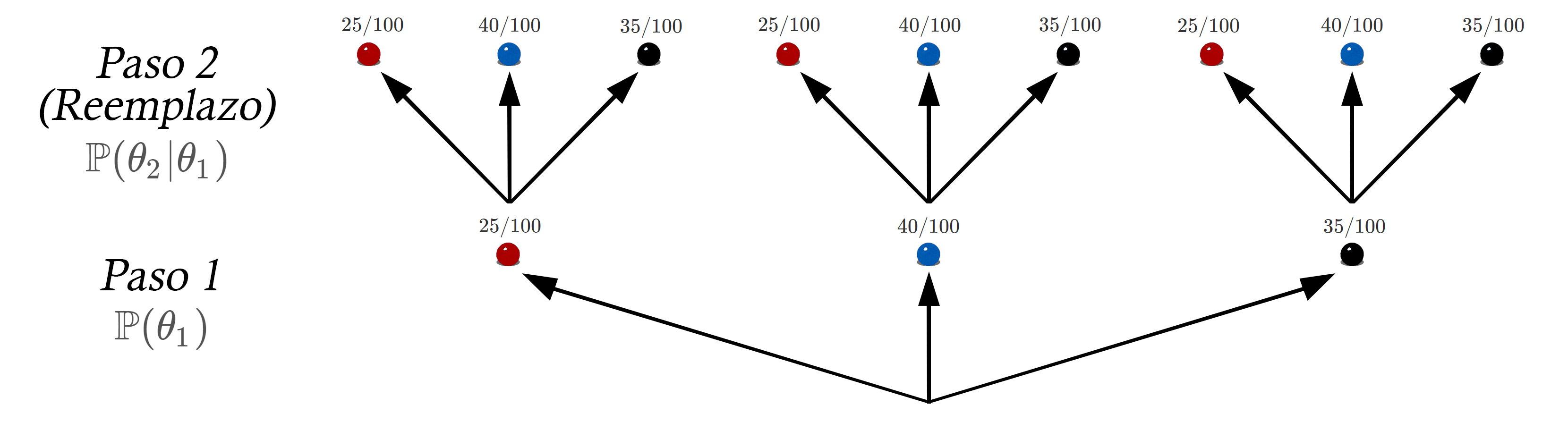
Para realizar el cálculo de la probabilidad de sacar una bola negra en el primer paso y una bola azul en el segundo paso, con reemplazo, se tendrá que \[\begin{align*} \mathbb{P}(N_1 \cap A_2) & = \mathbb{P}(N_1) \mathbb{P}(A_2 | N_1) \\ & = \frac{35}{100} \times \frac{40}{100} \\ &= \frac{1400}{10000} \\ &= 0.14 \end{align*}\] Encontrando entonces que la probabilidad de sacar una bola Negra en el primer paso y una bola azul en el segundo paso es del \(14\%\).
Ahora, para saber si los eventos planteados son o no independientes, podemos centrarnos en la primera linea, en donde tenemos que la probabilidad de sacar una bola negra es de \(\mathbb{P}(N_1)= \frac{35}{100}\), mientras que la probabilidad de sacar una bola azul es de \(\mathbb{P}(A_1)=\frac{40}{100}\), y en consecuencia, al verificar la formula asociada a independencia entre eventos, tendremos que \[\begin{align*} \mathbb{P}(N_1 \cap A_2) & = \mathbb{P}(N_1) \mathbb{P}(A_1) \\ \frac{1400}{10000} & = \frac{35}{100} \times \frac{40}{100} \\ \frac{1400}{10000} & = \frac{1400}{10000} \\ 0.14 &= 0.14 \end{align*}\] Y por tanto, al verificar que la igualdad se cumple, se concluye que los eventos son independientes. -
Similar al punto anterior, pero con la diferencia a que se realizan
\(3\) pasos, en donde, luego de sacar la primera bola, se registra y se
reemplaza la bola con una del mismo color, pero al sacar la segunda
bola, no se realiza reemplazo antes de sacar la tercera bola, alterando
las probabilidades de cada una de las bolas dentro de la bolsa, tal como
se presenta en el siguiente escenario
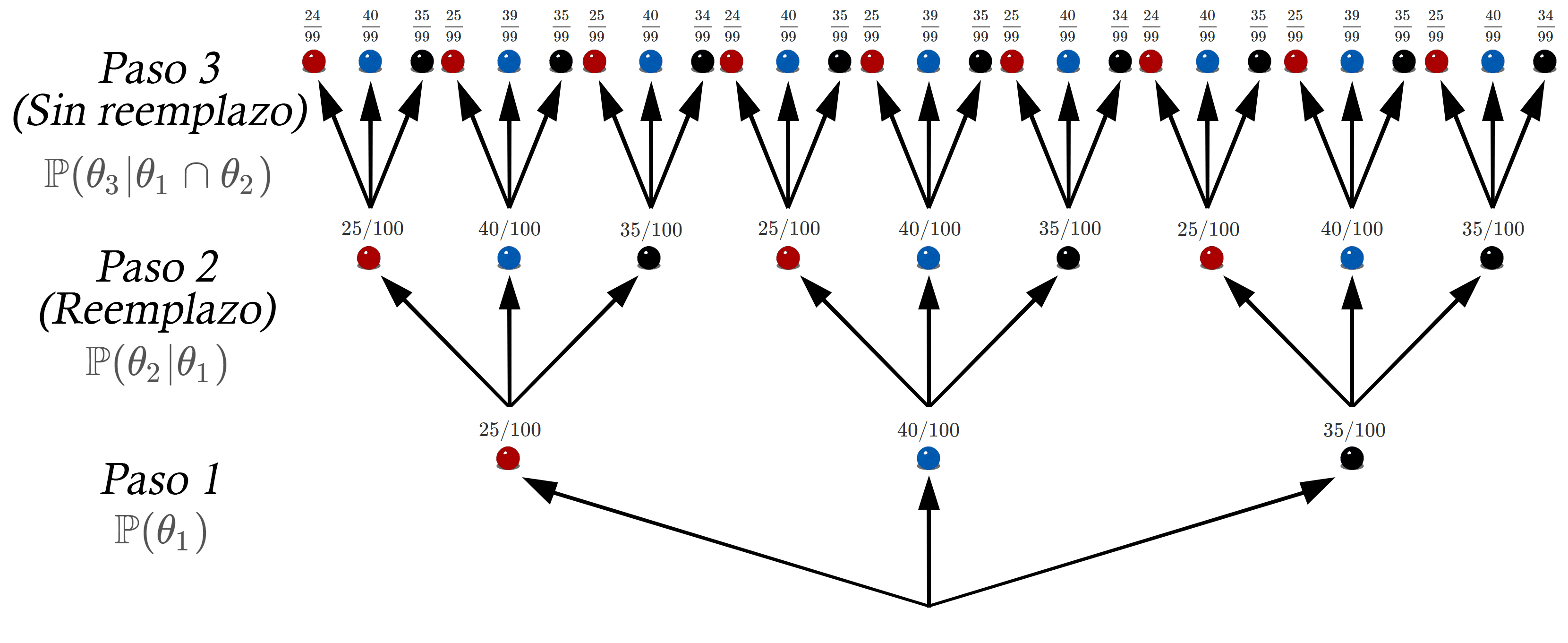
Al realizar el cálculo necesario para calcular la probabilidad de sacar una bola azul en el primer paso, una bola negra en el segundo paso y una bola roja en el tercero paso, tendremos que \[\begin{align*} \mathbb{P}(A_1 \cap N_2 \cap R_3) & = \mathbb{P}(A_1) \mathbb{P}(N_2 | A_1) \mathbb{P}(R_3 | A_1 \cap N_2) \\ &= \frac{40}{100} \times \frac{35}{100} \times \frac{25}{99} \\ &= \frac{35000}{990000} \\ &= 0.03535354 \end{align*}\] Ahora, para saber si los eventos planteados son o no independientes, podemos centrarnos en la primera linea, en donde tenemos que la probabilidad de sacar una bola negra es de \(\mathbb{P}(N_1)= \frac{35}{100}\), sacar una bola azul es de \(\mathbb{P}(A_1)=\frac{40}{100}\), y sacar una bola roja es de \(\mathbb{P}(R_1)= \frac{25}{100}\), y en consecuencia, al verificar la formula asociada a independencia entre eventos, tendremos que \[\begin{align*} \mathbb{P}(A_1 \cap N_2 \cap R_3) & = \mathbb{P}(A_1) \mathbb{P}(N_1) \mathbb{P}(R_1) \\ \frac{35000}{990000} & = \frac{35}{100} \times \frac{40}{100} \times \frac{25}{100} \\ \frac{35000}{990000} & = \frac{35000}{1000000} \\ 0.03535354 &\neq 0.035 \end{align*}\] Y por tanto, al verificar que la igualdad NO se cumple, se concluye que los eventos NO son independientes.
Probabilidad total
Sean $A_1, A_2, \ldots, A_k$ eventos mutuamente excluyentes
$(A_i\cap A_j = \oslash, \text{ para } i\neq j)$ y exhaustivos
$\left(\underset{i=1}{\stackrel{k}{\cup}} A_i = S\right)$, entonces
para cualquier otro evento $B$
\begin{align*} \mathbb{P}(B) &= \mathbb P(B\cap A_1)+\mathbb P(B\cap A_2)+\ldots+\mathbb P(B\cap A_k) \end{align*}
o alternativamente, al aplicar la formula de la
Regla
multiplicativa, tenemos que
\begin{align*} \mathbb{P}(B) &= \mathbb P(A_1)\mathbb P(B|A_1)+\mathbb P(A_2)\mathbb P(B|A_2)+\ldots+\mathbb P(A_k)\mathbb P(B|A_k) \end{align*}
Ejercicio
Tres máquinas de cierta planta de ensamble \(A_1, A_2, A_3\) montan
\(30\%, 45\%, 25\%\) del total de los productos producidos por la
empresa, respectivamente. Se sabe por experiencia que \(4\%, 5\%, 2\%\)
de los productos ensamblados por cada maquina tienen defectos,
respectivamente.
Si selecciona de forma aleatoria un producto terminado. Cuál es la
probabilidad de que éste se encuentra defectuoso?
\(B\): El producto se encuentra defectuoso.
\(A_1\): el producto
fue producido por la máquina \(1\).
\(A_2\): el producto fue
producido por la máquina \(2\).
\(A_3\): el producto fue producido
por la máquina \(3\).
Solución
Dado que el interés radica en encontrar la probabilidad de que se
seleccione un producto y resulte defectuoso, entonces nos están pidiendo
que se desea calcular la \(\mathbb{P}(B)\).
Como entre la información dada en el enunciado no nos da la probabilidad
de que un artículo se encuentre defectuoso, entonces podemos tratar de
calcularla mediante el teorema de probabilidad total, aprovechando que
los eventos \(A_1, A_2, A_3\) son eventos mutuamente
excluyentes (Un artículo que es ensamblado por una máquina, no
puede ser ensamblado simultáneamente por otra),
exhaustivos (El total de los productos ensamblados por
la empresa, solo puede ser producido por alguna de estas tres máquinas)
y que nos están dando las probabilidades de los eventos \(B|A_1\),
\(B|A_2\) y \(B|A_3\).
Partiendo de esto tenemos las siguientes probabilidades:
\[\begin{align*}
\mathbb{P}(A_1) & = 0.30 \\
\mathbb{P}(A_2) & = 0.45 \\
\mathbb{P}(A_3) & = 0.25 \\
\mathbb{P}(B | A_1) & = 0.04 \\
\mathbb{P}(B | A_2) & = 0.05 \\
\mathbb{P}(B | A_3) & = 0.02 \\
\end{align*}\]
Entonces, al aplicar el teorema de probabilidad total, tendremos que
\[\begin{align*}
\mathbb{P}(B) & = \mathbb{P}(A_1)\mathbb{P}(B | A_1) + \mathbb{P}(A_2)\mathbb{P}(B | A_2) + \mathbb{P}(A_3)\mathbb{P}(B | A_3) \\
& = 0.30 \times 0.04 + 0.45 \times 0.05 + 0.25 \times 0.02\\
& = 0.0395
\end{align*}\]
Obteniendo por tanto, que la probabilidad de que un artículo producido
en la empresa sea defectuoso es del \(3.95\%\)
Teorema de Bayes
Sea $A_1, A_2, \ldots, A_k$ eventos mutuamente excluyentes y
exhaustivos, con probabilidades previas $\mathbb P(A_i)$, para
$i=1,2,\ldots,k$, entonces para cualquier evento $B$ para el cual
$\mathbb P(B)>0$, la probabilidad posterior $A_j$ dado que $B$ ha
ocurrido, está dada por
\begin{align*} \mathbb P(A_j|B) &= \frac{\mathbb P(A_j\cap B)}{\mathbb P(B)} \\ \end{align*}
En donde, al aplicar la formula de la Regla multiplicativa en el numerador, y la formula de la Probabilidad total en el denominador, tenemos que
\begin{align*} \mathbb P(A_j|B) &= \frac{\mathbb P(A_j)\mathbb P(B|A_j)}{\sum_{i=1}^k \mathbb P(A_i)\mathbb P(B|A_i)} \end{align*}
Ejercicio
Tres máquinas de cierta planta de ensamble \(A_1, A_2, A_3\) montan
\(30\%, 45\%, 25\%\) del total de los productos producidos por la
empresa, respectivamente. Se sabe por experiencia que \(4\%, 5\%, 2\%\)
de los productos ensamblados por cada maquina tienen defectos,
respectivamente.
Si selecciona de forma aleatoria un producto terminado y se encuentra
que es defectuoso, Cuál es la probabilidad de que éste artículo haya
sido ensamblado por la máquina \(3\)?
\(B\): El producto se encuentra defectuoso.
\(A_1\): el producto
fue producido por la máquina \(1\).
\(A_2\): el producto fue
producido por la máquina \(2\).
\(A_3\): el producto fue producido
por la máquina \(3\).
Solución
En este caso, se tiene interés en saber la probabilidad de que un
artículo haya sido ensamblado por la máquina \(3\), \(A_3\),
dado que se sabe que el artículo seleccionado esta
defectuoso, \(B\), se tendrá que se desea calcular la
\(\mathbb{P}{(A_3|B)}\).
De lo anterior apreciamos que nos están preguntando una probabilidad
condicional la cual se puede expresar de la forma \[\begin{align*}
\mathbb{P}{(A_3|B)} & = \frac{\mathbb{P}(A_3 \cap B)}{\mathbb{P}(B)}
\end{align*}\]
El problema, es que al observar las probabilidades necesarias para
realizar el cálculo de la formula anterior vemos que no poseemos ninguna
de las dos probabilidades que necesitamos para llevar a cabo el cálculo
de interés.
Al detallar la ecuación más detenidamente, observamos que los eventos
\(A_1, A_2, A_3\) son mutuamente excluyentes y
exhaustivos, lo cual nos permite poder calcular la
\(\mathbb{P}(B)\) mediante el teorema de
Probabilidad
total, y la probabilidad \(\mathbb{P}(A_3 \cap B)\) mediante el
teorema de la
Regla
multiplicativa. Lo cual nos lleva a la siguiente expresión.
\[\begin{align*}
\mathbb{P}{(A_3|B)} & = \frac{\mathbb{P}(A_3)\mathbb{P}(B|A_3)}{\mathbb{P}(A_1)\mathbb{P}(B|A_1)+\mathbb{P}(A_2)\mathbb{P}(B|A_2)+\mathbb{P}(A_3)\mathbb{P}(B|A_3)} \\
& = \frac{0.25\times 0.02}{0.30\times 0.04 + 0.45\times 0.05 + 0.25\times 0.02} \\
& = \frac{0.005}{0.0395} \\
& = 0.1265823
\end{align*}\]
Es decir, se tiene que la probabilidad de que un artículo que se sabe
está defectuoso, haya sido ensamblado por la máquina \(3\), es del
\(12.69\%.\)