Caso de estudio
Para ilustrar como realizar los diferentes métodos de resúmenes numéricos, tabulares y gráficos, se empleará la siguiente base de datos de EjemploDescriptiva, la cual contiene las siguientes variables
- Municipio: Municipio de residencia de la persona.
- Estrato: Estrato socioeconómico de la vivienda.
- Edad: Edad de la persona en años.
- Altura: Altura de la persona en metros.
- Peso: Peso de la persona en kilogramos.
- Salario: Salario devengado por la persona en pesos.
- SatisTrabajo: Nivel de satisfacción con el trabajo actual.
- DeporFavorito: Deporte favorito de la persona.
Los datos contenidos en la base de datos se presentan a continuación:
| Municipio | Estrato | Edad | Altura | Peso | Salario | SatisTrabajo | DeporFavorito |
|---|---|---|---|---|---|---|---|
| Caldas | 5 | 17 | 1.77 | 66 | 1635100 | Muy satisfecho | Fútbol |
| Bello | 4 | 27 | 1.65 | 90 | 1752500 | Insatisfecho | Fútbol |
| Medellín | 1 | 18 | 1.57 | 66 | 1858400 | Satisfecho | Baloncesto |
| Caldas | 4 | 22 | 1.84 | 87 | 2131400 | Muy satisfecho | Fútbol |
| La Estrella | 3 | 20 | 1.86 | 89 | 1874800 | Satisfecho | Tenis |
| Caldas | 3 | 22 | 1.74 | 90 | 2933100 | Muy satisfecho | Fútbol |
| Itagüí | 1 | 20 | 1.91 | 79 | 1637200 | Muy insatisfecho | Fútbol |
| La Estrella | 3 | 27 | 1.77 | 88 | 1171200 | Indiferente | Baloncesto |
| Itagüí | 2 | 20 | 1.58 | 61 | 2574700 | Muy satisfecho | Baloncesto |
| Bello | 4 | 39 | 1.81 | 70 | 2739000 | Satisfecho | Tenis |
| La Estrella | 6 | 16 | 1.69 | 78 | 2887800 | Indiferente | Baloncesto |
| Bello | 2 | 40 | 1.93 | 83 | 2559600 | Muy satisfecho | Fútbol |
| Medellín | 2 | 26 | 1.93 | 91 | 1906600 | Satisfecho | Fútbol |
| Medellín | 2 | 21 | 1.87 | 61 | 1299700 | Satisfecho | Baloncesto |
| Bello | 4 | 23 | 1.60 | 84 | 1950900 | Indiferente | Fútbol |
| Itagüí | 3 | 40 | 1.91 | 76 | 2131900 | Satisfecho | Fútbol |
| La Estrella | 6 | 31 | 1.79 | 66 | 1085400 | Indiferente | Voleibol |
| La Estrella | 3 | 40 | 1.60 | 67 | 1182200 | Indiferente | Tenis |
| Medellín | 2 | 32 | 1.60 | 88 | 2541900 | Indiferente | Baloncesto |
| Caldas | 3 | 33 | 1.81 | 65 | 1333200 | Muy satisfecho | Fútbol |
Análisis gráfico
Un aspecto importante del análisis descriptivo, es el que se realiza mediante análisis gráfico. El análisis gráfico es una forma de simplificar lo tedioso y complejo de un conjunto de observaciones, además de ser una forma más accesible de presentación de la información cuando se tienen muchas variables, puesto que permiten mostrar el comportamiento de los datos presentados, y hacer juicios respecto a su tendencia central, variabilidad, formas, patrones, tendencias, etc.
El análisis gráfico, puede ser dividido en
- Gráficos para variables cuantitativa
- Gráficos para variables cualitativas
- Gráficos para cruces entre variables cuantitativas y cualitativas
En la siguiente tabla se hace un resumen de qué gráficos pueden ser apropiados para usar en cada uno de los casos
Una variable cuantitativa
Diagrama de tallo y hojas
Este gráfico sirve como medida de resumen de los datos, brinda información de valores máximos, mínimos, área en donde más se centran los datos, dispersión, datos atípicos y asimetría. A pesar de toda la información que puede brindar esta gráfica, su uso es muy limitado, ya que en situaciones en las cuales el rango de la variable es muy grande, ésta no permite visualidad con claridad dichos comportamientos. Este gráfico puede ser realizado mediante la función stem() de la librería graphics de la base del R.
Diagrama de tallo y hojas
# Construcción de diagrama de tallo y hojas
stem(datos$Edad)
The decimal point is 1 digit(s) to the right of the |
1 | 678
2 | 0001223
2 | 677
3 | 123
3 | 9
4 | 000
Interpretación
En el diagrama de tallo y hojas se aprecia que la edad mínima de los encuestados es de \(16\) años, mientras que la mayor es de \(40\), adicionalmente, se aprecia que la edad posee un comportamiento similar en \(20\) y \(40\) años, donde se aprecian \(3\) ocurrencias para cada valor. También se aprecia un comportamiento asimétrico positivo, en donde se aprecia que el conjunto de las edad se encuentra más reunida para edades más bajas que para edades más altas.
Gráfico de caja y bigotes
Este gráfico sirve para presentar de forma visual, datos numéricos a través de sus cuartiles, además de presentar otras características importantes, tales como el valor de los cuartiles, dispersión, simetría y datos potencialmente atípicos.
Representación de un Gráfico de Caja y Bigotes
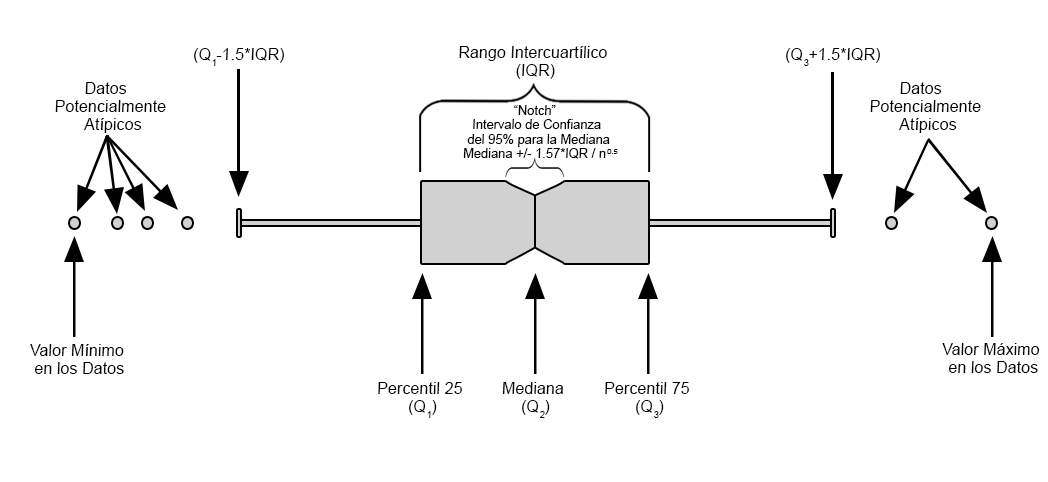
Este gráfico puede ser realizado mediante la función boxplot() de la librería graphics de la base del R.
Gráfico de caja y bigotes
# Construcción de gráfico de caja y bigotes
boxplot(datos$Peso, horizontal = T, xlab = "Peso (kg)", main = "Boxplot del Peso de las Personas",
col = "lightblue")
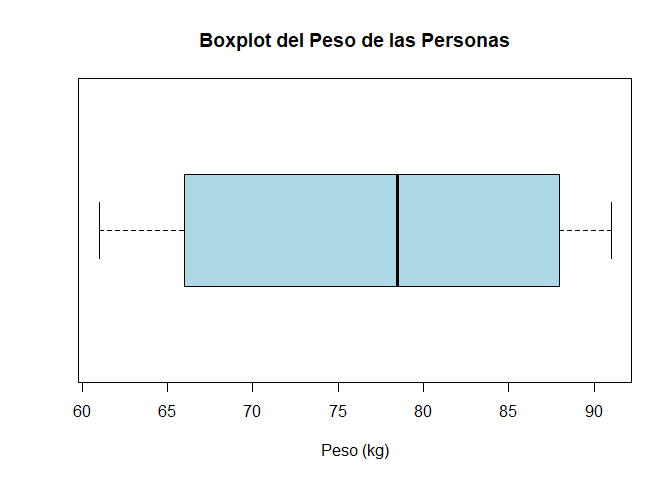
Interpretación
En el diagrama de caja y bigotes se aprecia que la mediana del peso de las personas se encuentra alrededor de \(79\) kg, en donde el primer y tercer cuartil se encuentran cercanos a \(66\) y \(88\) kg, respectivamente. No se aprecian observaciones extremas por fuera de los bigotes del gráfico y se observa un comportamiento asimétrico negativo, pues se aprecia que la mediana se encuentra más cercana al tercer cuartil que al primero. Finalmente se evidencia que la caja del gráfico es relativamente grande, presentando un rango intercuartílico cercano a \(22\) kg, lo cual podría considerarse como evidencia sobre que los datos poseen una gran dispersión.
Histograma
Este gráfico muestra la distribución de frecuencia o densidades del grupo de observaciones, brinda información sobre el valor más probables, la dispersión, la asimetría y valores extremos. Adicionalmente, tiene la ventaja de que su interpretación es muy intuitiva y por tanto es de los gráficos más preferidos para resumir información. Este gráfico puede ser realizado mediante la función hist() de la librería graphics de la base del R.
Histograma
## Construcción de histograma de frecuencias
hist(datos$Altura, main = "Histograma de Altura de las Personas", xlab = "Altura (m)",
col = "lightblue", freq = T)
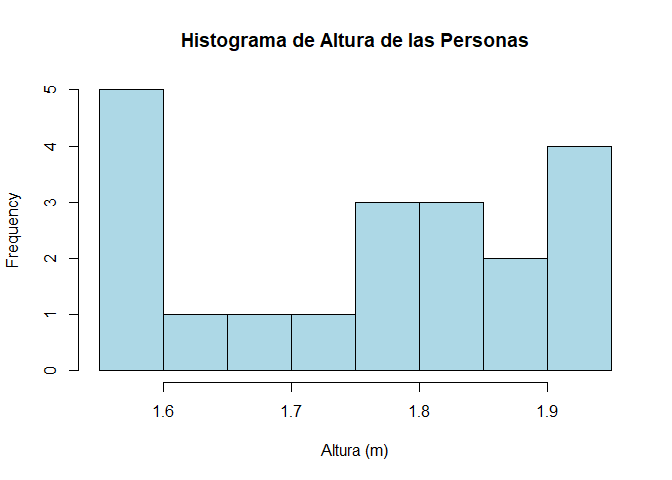
Interpretación
En la figura anterior, se aprecia que el histograma realiza una
agrupación de personas por categorías, con diferencia de cada una de
\(0.05\) metros de diferencia, en donde se evidencia que la categoría
para la altura entre \(1.55-1.60\) metros, es la que posee mayor
frecuencia con un total de \(5\) entradas. También se puede observar que
gran parte de las observaciones están reunidas en la parte derecha del
histograma, y en consecuencia, se podría pensar que el conjunto de
alturas posee una asimetría negativa.
Adicionalmente, al ser
una variable de altura de personas, y ver que hay personas que pueden
medir desde \(1.55-1.60\) metros hasta \(1.90-1.95\), entonces se
considera que la dispersión de las alturas es relativamente alta, lo
cual podría ser corroborarse mediante un análisis numérico. Finalmente,
como se aprecia que hay varias observaciones en las dos categorías
extremas, no se considerará que hayan observaciones extremas en el
conjunto de alturas recaudadas en la encuesta.
Densidad
Este gráfico funciona similar al histograma de densidades, con la diferencia de que en lugar de mostrar la distribución mediante clases (barras), éste muestra el comportamiento de la distribución de las observaciones mediante una curva. Dicha curva, brinda mayor información que el histograma respecto al valor promedio, dispersión y asimetría. Este gráfico puede ser realizado mediante la combinación de las funciones plot() y density(), de la forma plot(density()), siendo plot() y density() funciones de las librerías graphics y stats de la base de R.
Adicionalmente se presenta la función polygon de la librería graphics de la base de R, la cual sirve para generar formas, o en este caso, darle color a la densidad.
Densidad
## Construcción de la densidad
plot(density(datos$Salario), main = "Densidad de Salario de las Personas", xlab = "Salario (Pesos)",
lwd = 2)
# Colorea la densidad
polygon(density(datos$Salario), col = "lightblue")
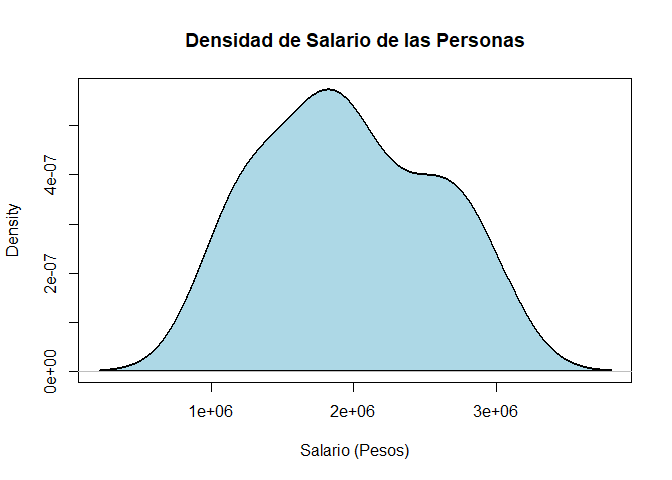
Interpretación
En el gráfico de densidad, se aprecia un comportamiento relativamente
simétrico, y por tanto se tendrá que el promedio de los salarios de los
encuestados debe estar alrededor de \(2\) millones de pesos, con una
desviación estándar de aproximadamente \(500\) mil pesos.
En la
distribución de los salarios no se aprecian colas pesadas (valores
extremos), a excepción de que hay algunos valores que se encuentran por
debajo del salario mínimo, lo cual podría ser explicado si se tuviera
información sobre el número de horas de trabajo de las personas, ya que
podría ser que en algunos casos podría deberse a que se trabaja medio
tiempo o menos horas.
Dos variables cuantitativas
Gráfico de dispersión
Este gráfico se emplea para hacer cruces entre dos variables cuantitativas, y sirve para ver tendencias y relaciones entre dos variables cuantitativas, además de permitir apreciar donde se centra el total de observaciones, y detección de datos atípicos dados dos atributos cuantitativos. Este gráfico puede ser realizado mediante la función plot() de la librería graphics de la base del R.
Gráfico de dispersión
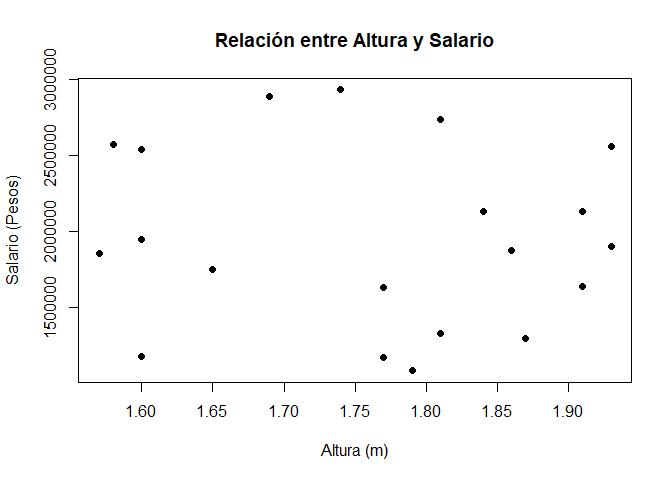
plot(x = datos$Altura, y = datos$Salario, xlab = "Altura (m)", ylab = "Salario (Pesos)",
main = "Relación entre Altura y Salario", pch = 19)
Interpretación
En el gráfico de dispersión anterior, no se aprecia ninguna relación clara entre la altura de las personas y el salario que devengan, pues no es posible observar que el conjunto de observaciones tenga alguna tendencia que apunte a una dirección en particular. Adicionalmente, se aprecia una gran dispersión entre el conjunto de observaciones, lo cual no hace posible la detección de datos atípicos entre los puntos.
Más de dos variables cuantitativas
Matriz de dispersión
Cuando se poseen más de dos variables cuantitativas, es posible presentar un matriz que muestre el cruce entre pares de variables, mediante cuadros con versiones simples de la función plot(). Este gráfico puede ser realizado mediante la función pairs() de la librería graphics de la base de R.
Matriz de dispersión básica
## Matriz de dispersión básica
pairs(cbind(datos$Edad, datos$Altura, datos$Peso), labels = c("Edad (Años)",
"Altura (m)", "Peso (kg)"))
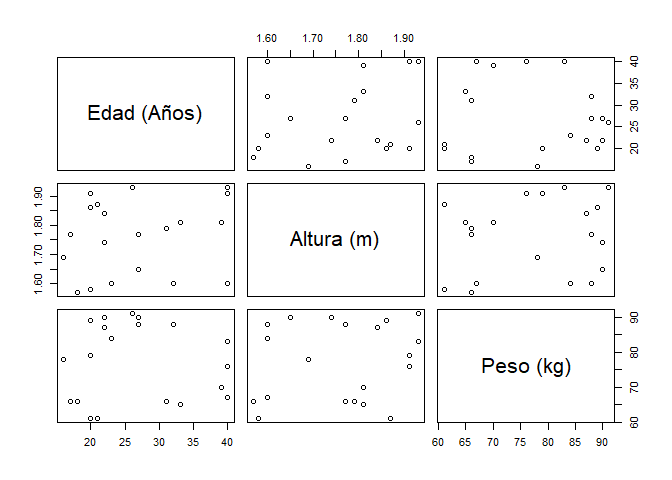
Interpretación
La matriz de dispersión, no se evidencia relación entre los pares de variables evaluadas, debido a que no es posible apreciar tendencias que apunten a alguna dirección en particular, o aglomeración de observaciones. Adicionalmente, se aprecia gran dispersión entre el conjunto de observaciones, y en consecuencia, no es posible detectar observaciones extremas.
Matriz de dispersión avanzada
Funciones complementarias pueden ser desarrolladas para mejorar la visualización los pares de variables. En el libro de Hernández & Correa (2018, pp. 40-49), se presentan diferentes funciones que pueden ser implementadas. Entre ellas
Hernández & Correa ([2018](#ref-Hernandez2018))
# Función para dibujar la dispersión y agregar la recta de regresión
panel.reg <- function(x, y) {
points(x, y, pch = 20)
abline(lm(y ~ x), lwd = 2, col = "dodgerblue2")
}
# Función para crear el histograma
panel.hist <- function(x, ...) {
usr <- par("usr")
on.exit(par(usr))
par(usr = c(usr[1:2], 0, 1.5))
h <- hist(x, plot = FALSE)
breaks <- h$breaks
nB <- length(breaks)
y <- h$counts
y <- y/max(y)
rect(breaks[-nB], 0, breaks[-1], y, col = "dodgerblue2", ...)
}
# Función para obtener la correlación
panel.cor <- function(x, y, digits = 2, prefix = "", cex.cor) {
usr <- par("usr")
on.exit(par(usr))
par(usr = c(0, 1, 0, 1))
r <- abs(cor(x, y))
txt <- format(c(r, 0.123456789), digits = digits)[1]
txt <- paste(prefix, txt, sep = "")
if (missing(cex.cor))
cex <- 0.8/strwidth(txt)
text(0.5, 0.5, txt, cex = cex * r)
}
pairs(cbind(datos$Edad, datos$Altura, datos$Peso), labels = c("Edad (Años)",
"Altura (m)", "Peso (kg)"), upper.panel = panel.reg, diag.panel = panel.hist,
lower.panel = panel.cor)
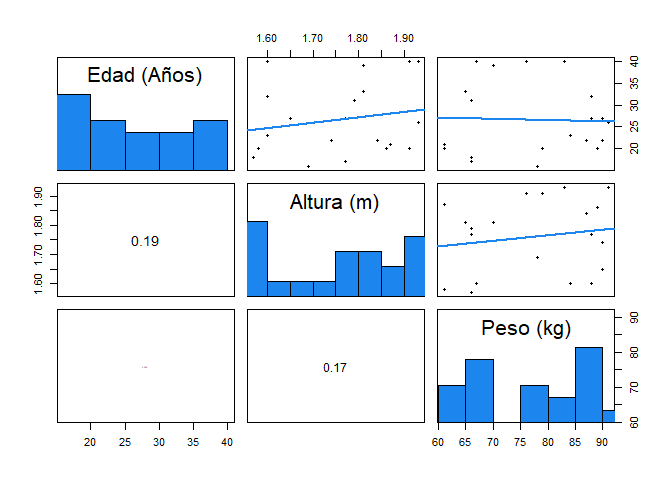
Interpretación
En la matriz de dispersión mejoradas, es posible observar un poco más de
información al respecto al conjunto de observaciones. Inicialmente,
vemos en la diagonal un histograma de cada variable individual, en donde
para la Edad, se aprecia que cada barra está compuesta por bloques de
\(5\) años, mostrando que la mayor proporción de personas posee menos de
\(20\) años, seguido por personas entre \(35-40\) años, también se
aprecia un comportamiento decreciente entre las edades, lo cual podría
pensarse en una forma asimetría ligeramente positiva.
Respecto
a la altura, vemos que cada barra está compuesta por bloques de \(0.05\)
metros de diferencia, comenzando en \(1.55-1.60\) metros y terminando en
\(1.95\) metros, en donde, se aprecia que la mayor proporción de
personas posee una altura menor a \(1.60\) metros, seguido por una
altura mayor a \(1.90\) metros. En ésta se observa una altura
relativamente simétrica, con una amplia dispersión.
Para el
peso, se observa que las barras del histograma saltan de \(5\) en \(5\)
kg, iniciando en \(60\) kg hasta \(95\), siendo la categoría \(85-90\)
kg la que posee mayor número de observaciones, seguida por la categoría
\(65-70\) kg. No se observan valores atípicos en el conjunto de los
pesos, dado los valores planteados son valores comúnmente alcanzables.
No es posible asegurar la existencia de una estructura asimétrica
definida, debido al comportamiento de las barras que no tiene
crecimientos ni decrecimientos uniformes.
En la parte inferior
izquierda, se muestran los valores asociados a la correlación entre cada
par de variables, en donde se observa que la correlación entre la Edad y
la Altura es de \(0.19\), entre la Altura y el Peso de \(0.17\) y entre
la Edad y el Peso de prácticamente \(0\). De lo anterior, si usamos los
valores de referencia presentados en la
Clase
02 sobre Medidas de Asociación, se tendrá que al tener una
correlación menores a \(30\%\), se concluirá que la correlación entre
cada uno de los pares de variables es débil o nula.
Finalmente,
en la parte superior derecha, se presenta el gráfico de dispersión entre
cada par de variables junto con su recta de regresión. En el gráfico
entre Edad y Altura, no se aprecia ninguna agregación de datos, alguna
relación positiva o negativa entre las variables o valores atípicos.
Comportamiento similar se observa entre los pares de variables de
Edad-Peso, y Altura-Peso.
Una variable cualitativa
Gráfico de barras
Sirve para resumir una o dos variables cualitativas mediante barras de frecuencias absolutas o relativas. Éste permite observar la concentración de observaciones en una o más categorías diferentes. Este gráfico puede ser realizado mediante la función barplot() de la librería graphics de la base de R.
Para realizar estas gráficas deben usarse como insumo, las tablas de frecuencias absolutas o relativas construidas previamente en la subsección de Resumen tabular.
Gráfico de barras una variable para frecuencias absoluta
# Gráfico de barras para una variable de frecuencias absolutas
barplot(tabla1via, main = "Frecuencias absolutas de los Municipios", col = hcl.colors(5))
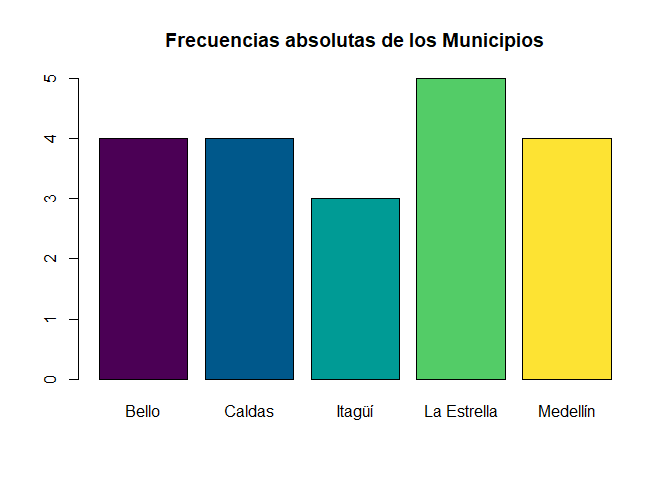
Interpretación
En el gráfico de barras, se observa que entre el total de los \(20\) encuestados, la mayoría con \(5\) personas viven en la Estrella, seguido por los municipios de Bello, Caldas y Medellín con un total de \(4\) personas, y el municipio de Itagüí con \(3\) personas encuestadas.
Gráfico de barras una variable para frecuencias relativas
# Gráfico de barras para una variable de frecuencias relativas
barplot(prop1via, main = "Frecuencias relativas de los Municipios", col = rainbow(5))
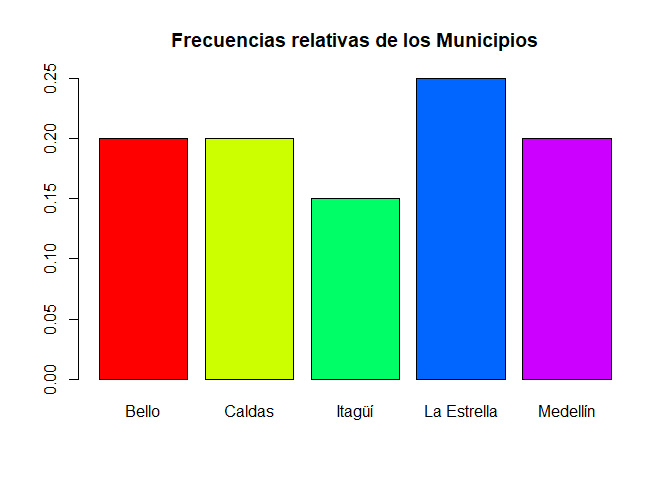
Interpretación
En el gráfico de barra anterior, se aprecia de forma visual el comportamiento de la proporción de encuestados respecto al municipio en donde viven, mostrando que en los municipios de Bello, Caldas y Medellín se realizó en cada una un \(20\%\) de las encuestas, mientras que en la Estrella e Itagüí se realizó un \(25\%\) y \(15\%\) de las encuestas respectivamente.
Gráfico de pareto
Este gráfico es similar al gráfico de barras para una sola variable cualitativa, pero con la ventaja de que presenta las frecuencias absolutas, relativas, y las frecuencias acumuladas absolutas y acumuladas relativas en el mismo gráfico. Este gráfico puede ser realizado mediante la función pareto.chart() de la librería qcc, usando como insumo las tablas de frecuencias absolutas construidas previamente en la subsección de Resumen tabular.
Gráfico de pareto una variable cualitativa
## Instalar y cargar
# install.packages('qcc') # Instala librería qcc
library(qcc) # Carga librería qcc
# Gráfico de pareto para una variable cualitativa
pareto.chart(tabla1via, main = "Gráfico Pareto para los Municipios")
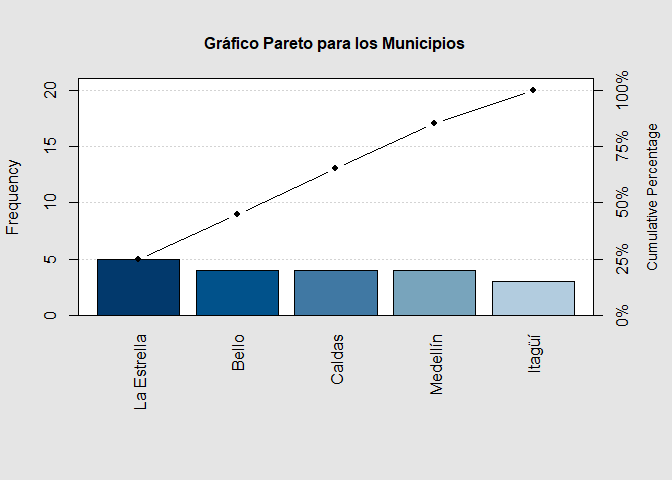
Pareto chart analysis for tabla1via
Frequency Cum.Freq. Percentage Cum.Percent.
La Estrella 5 5 25 25
Bello 4 9 20 45
Caldas 4 13 20 65
Medellín 4 17 20 85
Itagüí 3 20 15 100
Interpretación
El gráfico pareto anterior agregada diferente información sobre el
municipio de vivienda de las personas encuestadas, en donde, en el eje
izquierdo se observa el valor de las frecuencias absolutas, mientras que
en el eje derecho se observa el valor de las frecuencias relativas. Las
barras representan los valores absolutos o relativos, dependiendo del
eje (izquierdo o derecho) que se observe, mientras que los puntos
representan los valores acumulados absolutos o relativos dependiendo del
eje (izquierdo o derecho) que se observe.
Dicho comportamiento
es resumido en la tabla de análisis de pareto, en donde se presentan las
frecuencias-proporciones simples en orden descendente, desde la que
posee mayor cantidad, hasta la que posee una menor cantidad. En la tabla
de salida se observa que \(5\) personas que equivalen a \(25\%\) de los
datos totales habitan en la Estrella, \(4\) personas que equivalen a
\(20\%\) del total de la población habitan en Bello. Frecuencia y
proporción similar a Bello habitan en Caldas y Medellín. Finalmente, con
una frecuencia de \(3\) encuestados, que equivale a \(15\%\) del total
del total de los encuestados, habita en Itagüí.
Gráfico de pastel
Este gráfico también sirve para representar gráficamente las tablas de frecuencias absolutas y relativas para una variable cualitativa. A pesar de ser un gráfico ampliamente usado en la práctica, éste no muestra bien la información que se desea presentar, debido a que siempre debe estar acompañado de los porcentajes o frecuencias que representa cada área, ya que de otra forma, dicho gráfico puede ser muy engañoso.
Este gráfico puede ser realizado mediante la función pie() de la librería graphics de la base de R, usando como insumo, las tablas de frecuencias absolutas construidas previamente en la subsección de Resumen tabular.
Mientras que las etiquetas de los porcentajes o frecuencias de cada área, puede establecerse mediante la función legend() de la librería graphics de la base de R.
Gráfico de barras una variable para frecuencias absoluta
# Gráfico de pastel una variable de frecuencias absolutas
pie(tabla1via, main = "Frecuencias absolutas por Municipio", col = cm.colors(5))
legend("topleft", legend = round(prop1via, 4), fill = cm.colors(5))
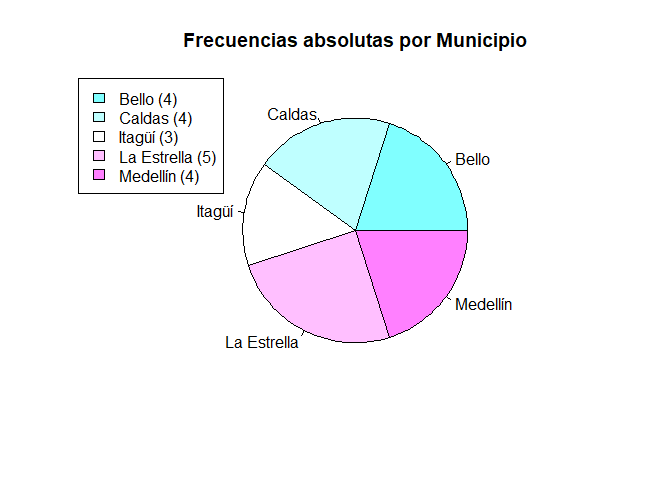
Interpretación
El gráfico de pastel anterior, muestra la frecuencia absoluta de encuestas que se realizaron por municipio, en donde triángulos más grandes representan una mayor frecuencia y triángulos más pequeños una menor frecuencia. Dado que no es posible saber con certeza si los triángulos son iguales o diferentes, se agrega en la parte izquierda un cuadro con el nombre de la categoría y la frecuencia absoluta entre paréntesis. En este cuadro, se aprecia que el municipio de la Estrella es quién posee la mayor frecuencia en la encuesta, con un total de \(5\) encuestados, seguidos por Bello, Caldas y Medellín con un total de \(4\) encuestados cada una, y seguido por \(3\) encuestados pertenecientes al municipio de Itagüí.
Gráfico de barras una variable para frecuencias relativas
# Gráfico de pastel una variable de frecuencias relativas
pie(prop1via, main = "Frecuencia Relativa por Municipio", col = hcl.colors(5))
legend("topleft", legend = round(prop1via, 4), fill = hcl.colors(5))
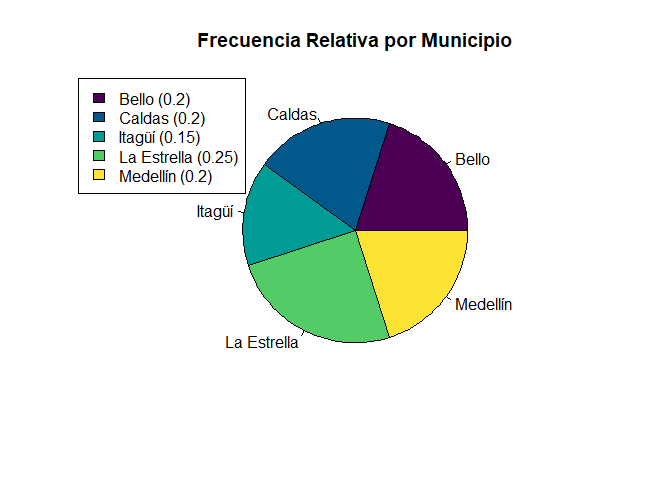
Interpretación
En el gráfico anterior, se presenta la proporción de encuestas realizadas en cada uno de los municipios de interés, en donde el gráfico de pastel representa el \(100\%\) de las encuesta realizadas, y cada triángulo la proporción asociada a cada uno de los municipios. En donde, como es difícil saber con certeza si los triángulos son o no iguales, se agrega la proporción asociada en la parte izquierda mediante un cuadro que muestra el nombre del municipio y la frecuencia relativa o proporción asociada entre paréntesis. En el cuadro se evidencia que la Estrella posee el \(25\%\) del total del diagrama del pastel, los municipios de Bello, Caldas y Medellín el \(20\%\) cada uno, y el municipio de Itagüí el \(15\%\) restante.
Gráfico de puntos
Este gráfico también es similar al gráfico de barras, sirve para presentar las frecuencias absolutas o relativas de una variable cualitativa, y muestra un punto que representa el conteo del total de observaciones que hay para cada variable. Este gráfico puede ser realizado mediante la función dotchart() de la librería graphics de la base de R, usando como insumo las tablas de frecuencias absolutas construidas previamente en la subsección de Resumen tabular.
Gráfico de puntos para una variable de frecuencias absolutas
# Gráfico de puntos para una variable de frecuencias absolutas
dotchart(tabla1via, main = "Frecuencias absolutas de categorías por Municipio")
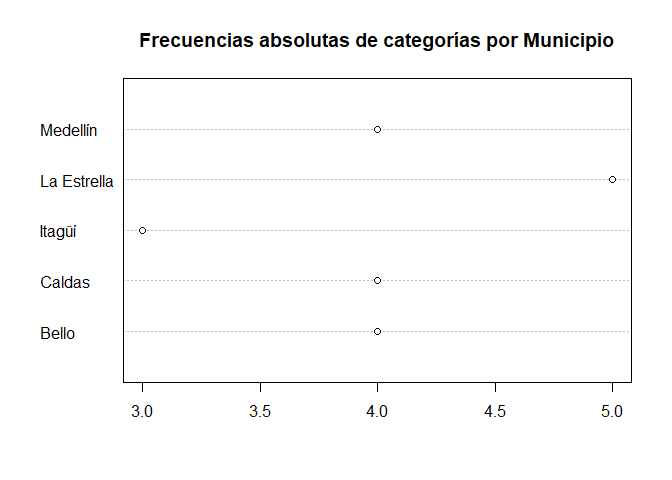
Interpretación
El gráfico de puntos, funciona similar al gráfico de barras solo que en lugar de mostrar barras para mostrar el valor que posee cada categoría, éste gráfico muestra un punto asociado a un valor, que puede evidenciarse en el eje inferior. El gráfico anterior muestra un punto para el valor de \(3\) en el caso de Itagüí, un valor de \(4\) en el caso de Bello, Caldas y Medellín, y un valor de \(5\) en el caso de la Estrella. Dichos valores representan el número de encuestados que hay en la base de datos.
Gráfico de puntos para una variable de frecuencias relativas
# Gráfico de puntos para una variable de frecuencias relativas
dotchart(prop1via, main = "Frecuencias relativas de categorías por Municipio")
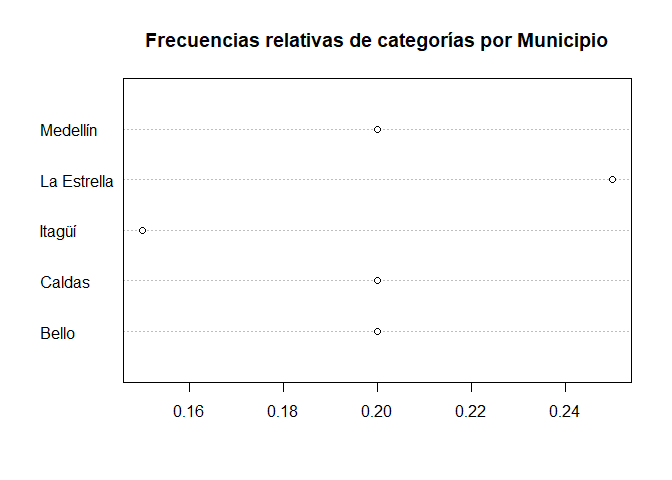
Interpretación
El gráfico de puntos también puede mostrar la proporción asociada en la categoría en el eje inferior. En este caso vemos que los valores en el eje van saltando de \(0.02\) en \(0.02\), y por ello, en este caso se tendrá que el municipio de Itagüí representa el \(15\%\) de todas todas las encuestas, Bello, Caldas y Bello cada uno representa el \(20\%\), y el municipio de la Estrella representa al \(25\%\) de la totalidad de las encuestas.
Dos variables cualitativas
Gráfico de barras
El gráfico de barras también sirve para resumir dos variable cualitativa mediante barras de frecuencias absolutas o relativas. La interpretación, será la misma que para una sola variable cualitativa, con la diferencia de que en este caso, se podrán hacer comparaciones por categorías adicionales. Este gráfico puede ser realizado mediante la función barplot() de la librería graphics de la base de R, junto a la función legend(), para establecer las etiquetas asociadas a cada una de las barras que se presenten en el gráfico.
Gráfico de barras dos variables para frecuencias absolutas
# Gráfico de barras para dos variables para frecuencias absolutas
barplot(tabla2vias, main = "Frecuencias absolutas categorías de Deporte por Municipio",
col = topo.colors(5), beside = T)
legend("topright", rownames(tabla2vias), fill = topo.colors(5))
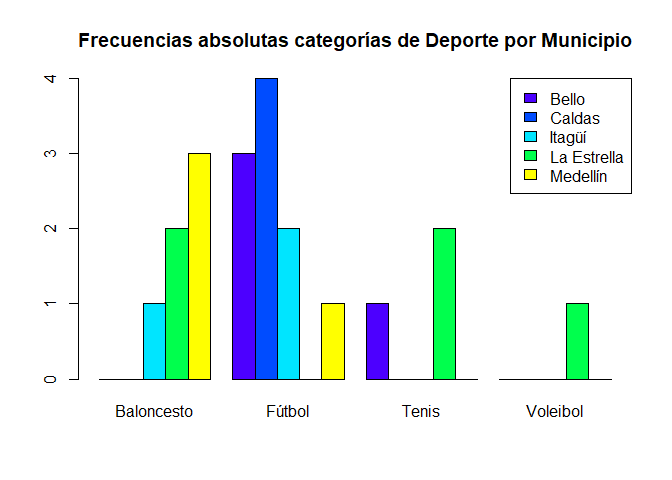
Interpretación
En el gráfico de barras para el cruce entre el deporte favorito y el municipio de vivienda, se observa que de las \(6\) personas que prefieren Baloncesto sobre otros deportes, hay \(3\) que residen en Medellín, \(2\) en la Estrella y \(1\) en Itagüí. Por su parte, de las \(10\) personas que prefieren el Fútbol, se aprecia que la mayoría de las personas habitan en Caldas, seguido por Bello, Itagüí y Medellín, con una frecuencia de \(4\), \(3\), \(2\) y \(1\) respectivamente. Para las \(3\) personas encuestadas que prefieren Tenis sobre otros deportes, se tiene que \(2\) viven en la Estrella y \(1\) en Bello, mientras que de los encuestados, solo una persona prefiere Voleibol sobre otros deportes, y éste reside en la Estrella.
Gráfico de barras dos variables para frecuencias relativas
# Gráfico de barras para dos variables para frecuencias relativas
barplot(prop2vias, main = "Frecuencias relativa categorías de Deporte por Municipio",
col = terrain.colors(5), beside = T)
legend("topright", rownames(prop2vias), fill = terrain.colors(5))
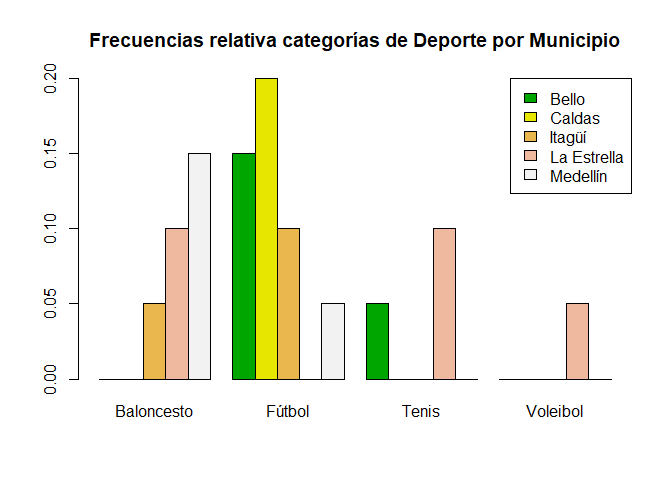
Interpretación
En el gráfico anterior, se ilustra el cruce entre las variables de deporte y municipio, y se observa que el \(30\%\) de los encuestados prefieren baloncesto sobre otros deportes, porcentaje que se divide entre \(15\%\) asociado a personas que habitan en Medellín, \(10\%\) que habitan en la Estrella y \(5\%\) en Itagüí. De forma similar, se aprecia que \(50\%\) de los encuestados prefieren el fútbol, de donde el \(20\%\) habitan en Caldas, \(15\%\) en Bello, \(10\%\) en Itagüí y \(5\%\) en Medellín. Para las personas que prefieren el Tenis y Voleibol sobre otros deportes, se tiene un \(15\%\) y \(5\%\), respectivamente, de donde, de los que prefieren el Tenis, el \(10\%\) habitan en la Estrella y \(5\%\) en Bello, mientras que, los que prefieren Voleibol habitan todos en la Estrella.
Gráfico de puntos
Como se señaló, este gráfico es similar al gráfico de barras, y sirve para resumir dos variable cualitativa a partir de sus frecuencias absolutas o relativas, y muestra un punto que representa el conteo del total de observaciones que hay para cada variable. Este gráfico puede ser realizado mediante la función dotchart() de la librería graphics de la base de R, usando como insumo las tablas de frecuencias absolutas construidas previamente en la subsección de Resumen tabular.
Gráfico de puntos para dos variables de frecuencias absolutas
# Gráfico de barras para dos variables para frecuencias absolutas
dotchart(tabla2vias, main = "Frecuencias absolutas de categorías de Deporte por Municipio")
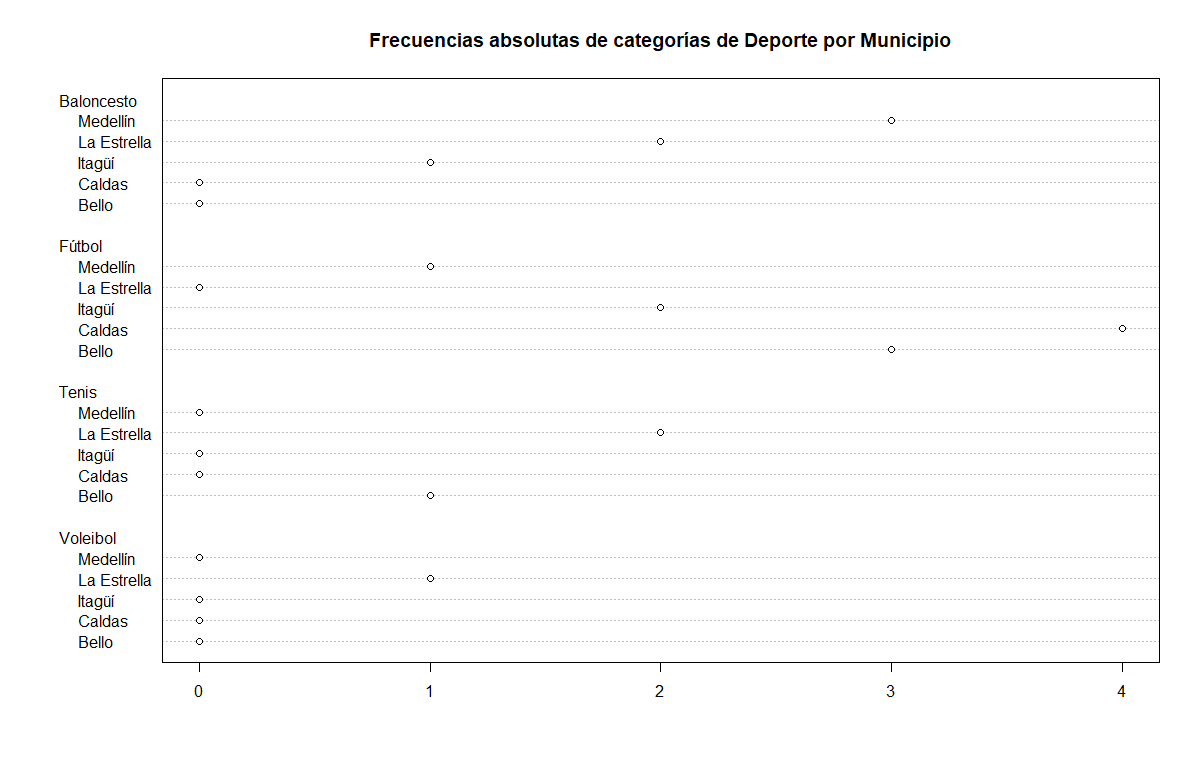
Interpretación
En el gráfico de puntos anterior, se observan las categorías de
municipio de vivienda anidadas dentro del deporte favorito de las
personas, en donde, para el deporte baloncesto, se aprecia en el eje
inferior, que \(3\) de ellos viven en Medellín, \(2\) en la Estrella y
\(1\) en Itagüí.
En el caso de quienes prefieren Fútbol se
observa la mayor cantidad de encuestados, en donde se tiene \(1\)
habitante con localidad en Medellín, \(2\) en Itagüí, \(4\) en Caldas y
\(3\) en Bello. Similarmente, para quienes prefieren practicar Tenis se
encuentran \(2\) personas que viven en la Estrella y \(2\) en Bello.
Finalmente, la única persona que prefiere el Voleibol sobre otros
deportes, se encuentra que vive en la Estrella.
Gráfico de puntos para dos variables de frecuencias relativas
# Gráfico de barras para dos variables para frecuencias relativas
dotchart(prop2vias, main = "Frecuencias relativas de categorías de Deporte por Municipio")
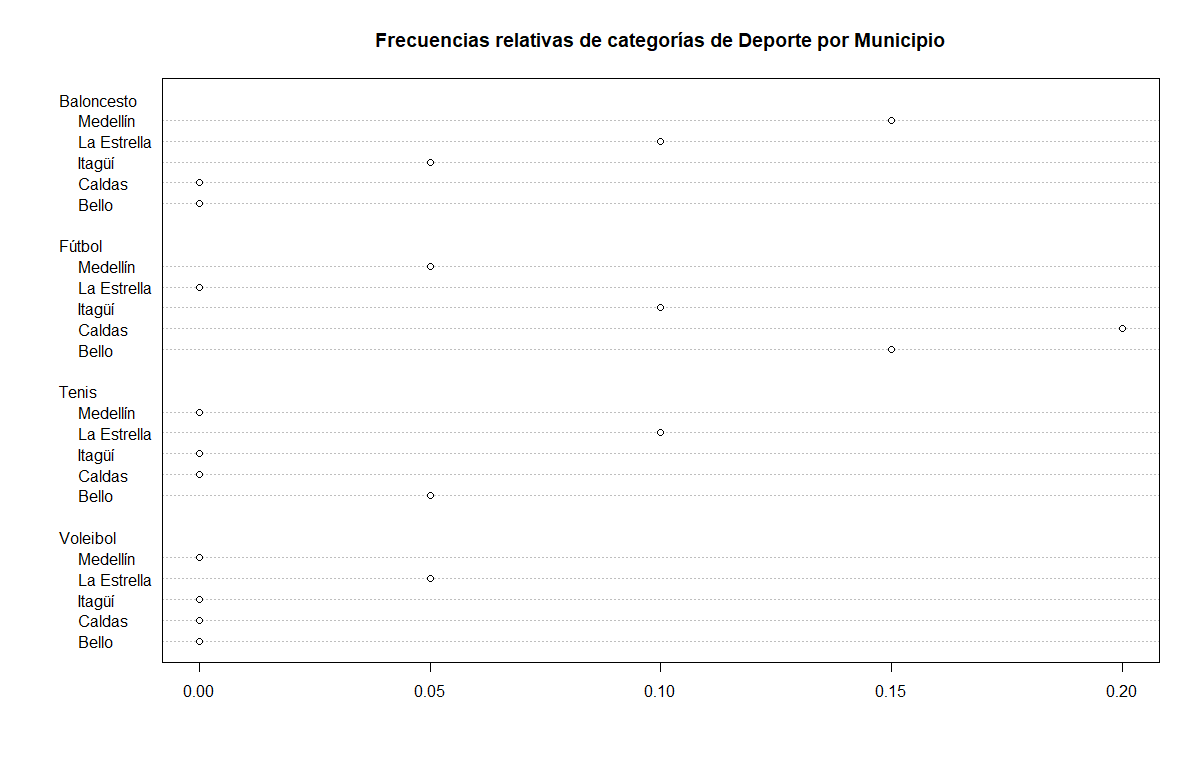
Interpretación
En el gráfico de puntos para frecuencias relativas, se aprecia un cruce
entre el municipio de vivienda y el deporte favorito de las personas en
el eje \(Y\), mientras la proporción asociada en el eje \(X\). Al
observar por deporte, encontramos que el deporte menos popular es el
voleibol con solo una persona que lo prefiere sobre los demás, la cual
vive en la Estrella y representa el \(5\%\) del totalidad de la
encuesta.
El deporte más popular es el fútbol con un total del
\(50\%\) de los encuestados los cuales se dividen entre \(5\%\) que
reside en la Estrella, \(10\%\) en Itagüí, \(20\%\) en Caldas y \(15\%\)
en Bello. También se presenta información sobre las personas que
prefieren baloncesto sobre otros deportes con un total de \(30\%\) de la
totalidad de las encuestas, porcentaje que se reparte entre Medellín, la
Estrella e Itagüí con el \(15\%\), \(10\%\) y \(5\%\), respectivamente.
Adicionalmente se evidencia que el \(15\%\) restante de los encuestados
prefieren el Tenis sobre otros deportes, siendo un \(10\%\) personas que
viven la Estrella y el \(5\%\) personas que viven en Bello.
Gráfico de balón
El gráfico de balón, suele ser un gráfico más avanzado para resumir dos variable cualitativa, en donde se establecen en el cruce de las dos variables, círculos que se asocian al tamaño del cruce de las dos variables cualitativas. Este gráfico puede ser realizado mediante la función ggballoonplot() de la librería ggpubr, la cual depende de la librería ggplot2.
Gráfico de balón
# Carga las librerías
library(ggplot2)
library(ggpubr)
# Establece un tema por defecto para el gráfico
theme_set(theme_pubr())
# Gráfico de balón
ggballoonplot(data.frame(tabla2vias), fill = "value") + scale_fill_viridis_c(option = "C")
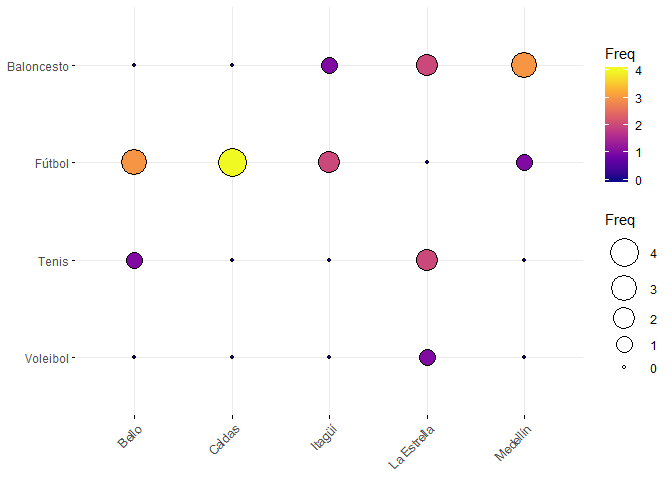
Interpretación
En el gráfico de balón, se muestra el número de observaciones que hay entre el cruce de las variables deporte y municipio. En dicho gráfico se observa que la mayor frecuencia de observaciones se da en el cruce entre los encuestados que viven en el municipio de Caldas y que prefieren el fútbol entre los demás deportes, con un tal de \(4\) observaciones, seguido por los cruces entre Bello-Fútbol y Medellín-Baloncesto con un total de \(3\) observaciones. Adicionalmente se observa que de todos los municipios, en el departamento de La Estrella, es donde se evidencia que hay personas que prefieren el Voleibol sobre los demás deportes.
Cualitativa - Cuantitativa
Gráfico de caja y bigotes
Este gráfico sirve para presentar de forma visual, datos numéricos por
categorías a través de sus cuartiles, además de presentar otras
características importantes, tales como la dispersión, simetría y datos
potencialmente atípicos. Este gráfico puede ser realizado mediante la
función boxplot() de la librería graphics de R.
Gráfico de caja y bigotes
# Construcción de gráfico de caja y bigotes por categorías
boxplot(datos$Altura ~ datos$Estrato, horizontal = T, xlab = "Altura (m)", ylab = "Estratos",
main = "Boxplot de Altura de las personas por Estrato", col = terrain.colors(6))
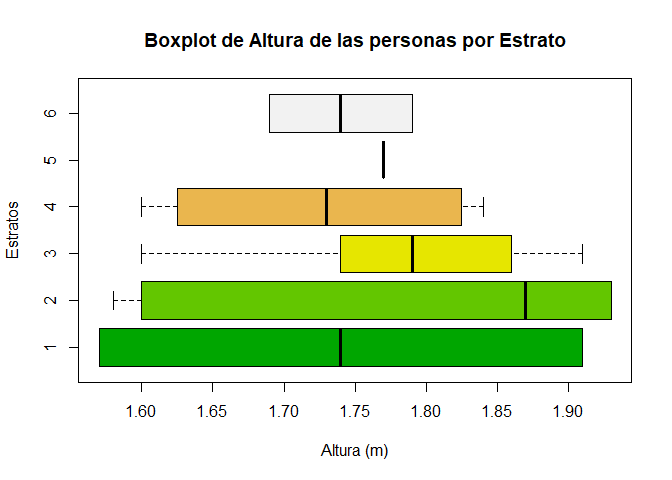
Interpretación
En el gráfico anterior, se hace una comparación entre la altura de los
encuestados y el estrato socioeconómico al que pertenece cada
encuestado. En éste se aprecia que de los \(6\) estratos, el estrato
\(2\) es el que posee la mayor mediana de estatura respecto a los demás
estratos.
También se observa que solo existe una observación
en el estrato \(5\), por lo cual solo se aprecia una barra vertical que
representa el valor de esa observación. Se evidencia además que la
mediana de la altura de los encuestados pertenecientes al estrato \(6\),
\(4\) y \(1\) poseen una mediana similar que ronda los \(1.74\) metros.
Asimismo, puede apreciarse que de los \(6\) estratos, los
estratos \(1\) y \(2\) poseen la mayor variabilidad entre todos los
estratos, pues son los que poseen mayor rango y mayor rango
intercuartílico. Se nota además, que para todos los estratos se observa
un comportamiento simétrico, a excepción del estrato \(2\), el cual
posee una asimetría negativa, dado que el valor de la mediana se
encuentra en la parte derecha de la caja.
Finalmente, puede
notarse que no se evidencia ningún punto a la derecha o izquierda de los
bigotes de las diferentes cajas, lo cual quiere decir, que no se
identificaron alturas extremas o atípicas para ninguno de los estratos
socioeconómicos.
Adicionalmente puede agregarse el argumento notch = TRUE, lo cual provoca una muesca en cada lado de la caja. McGill, Tukey, & Larsen (1978) señala que estas muescas representan un intervalo del 95% de confianza alrededor de la mediana, y que son construidas a partir de la ecuación
\begin{align*} \tilde{X}\pm 1.57\times \frac{IQR}{\sqrt{n}} \end{align*}
En donde, si las muescas de dos parcelas no se superponen, entonces se tendrá evidencia sólida respecto a que la mediana de los grupos es diferente (Chambers, Cleveland, Kleiner, & Tukey, 1983, p. 62).
Gráfico de caja y bigotes con intervalo de confianza del 95% para la mediana
# Construcción de diagrama de caja y bigotes por categorías con intervalo
# del 95% para la mediana
boxplot(datos$Altura ~ datos$Estrato, horizontal = T, xlab = "Altura (m)", ylab = "Estratos",
main = "Boxplot de Altura de las personas por Estrato", col = topo.colors(6),
notch = T)
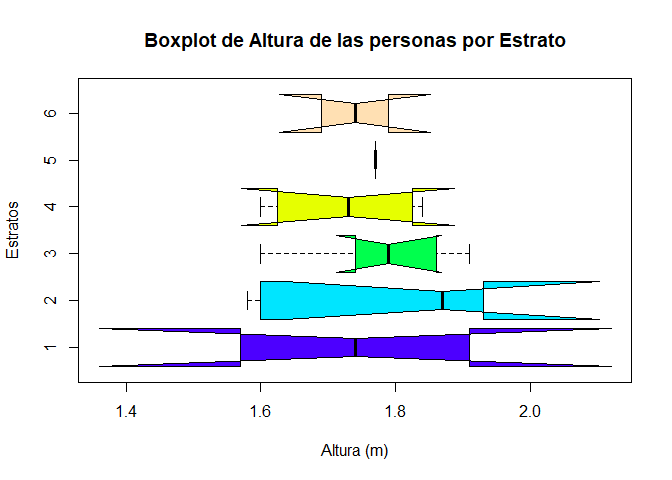
Interpretación
El gráfico de caja y bigotes, presentan un comparativo de la altura de
las personas con el estrato socioeconómico, adicionando además
intervalos de confianza para la mediana, con el fin de observar si las
medianas de cada estrato es significativamente diferente que el de otros
estratos o no.
En el gráfico se aprecia que en casi todos los
estratos se observa que las bandas de confianza son mayores al primer y
tercer cuartil, a excepción de los estratos \(5\) y \(2\) en donde, el
primero posee una sola observación, y en consecuencia sus bandas de
confianza son iguales a su mediana o único valor registrado, mientras
que, para el segundo se aprecia que la banda de confianza solo supera el
tercer cuartil.
Se evidencia que de las medianas presentadas,
las de los estratos \(6\), \(4\) y \(1\) son muy similares situándose
alrededor de \(1.74\) metros, mientras que el estrato que presenta una
mayor mediana es el \(2\) con un valor cercano a \(1.86\). La diferencia
entre la mediana de los estratos no parece ser significativamente
diferente aunque se aprecie que hay unos valores mayores o menores que
otros, debido a que los intervalos de confianza del \(95\%\) para la
mediana se traslapan unos con otros.
También se nota, que de
los estratos propuestos, la altura de los estratos \(1\) y \(2\) parecen
ser los que poseen la mayor variabilidad entre todas las categorías, ya
que se que tanto su rango, rango intercuartílico como bandas de
confianza son las más grandes. Es de anotar, que para ninguno de los
estratos se observan valores atípicos, ya que, para ninguno de las
categorías se identifican puntos por fuera de los bigotes de las cajas.
Gráfico de medias
Este gráfico sirve para presentar de forma visual, grupos de datos numéricos a través de sus media y desviación estándar. El gráfico está compuesto por un punto que representa el valor promedio del grupo de observaciones y las barras representan dos desviación estándar de la media. En donde, si las barras no se superponen, entonces se tendrá evidencia sólida respecto a que la media de los grupos es diferente.
Este gráfico puede ser realizado mediante la función plotMeans() de la librería RcmdrMisc.
Gráfico de medias
## Instalar y cargar librerías
# install.packages('RcmdrMisc') # Instala librería RcmdrMisc
library(RcmdrMisc) # Carga la librería RcmdrMisc
## Construcción de diagrama de caja y bigotes por categorías
# Recordar escribir en error.bars = 'conf.int' porque por defecto se
# presenta un intervalo para el error estándar y no para dos desviaciones estándar.
plotMeans(response = datos$Peso, factor1 = datos$Estrato, error.bars = "conf.int",
xlab = "Estrato", ylab = "Peso (kg)", main = "Plot of Means de Peso de las personas por Estrato")
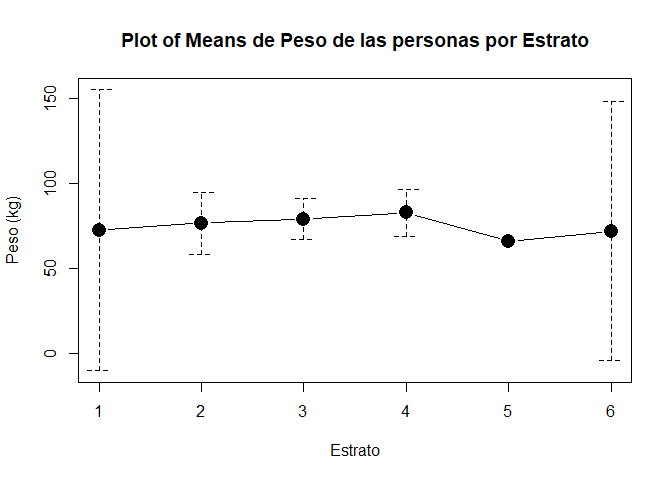
Interpretación
A diferencia del gráfico de caja y bigotes, el gráfico de medias muestra
el valor promedio del conjunto de observaciones por cada grupo de
interés, junto con sus respectivos intervalos de confianza del \(95\%\)
para la media, para poder observar si hay diferencias significativas
entre una categorías y otra.
Del gráfico anterior, se evidencia
que el peso promedio de las personas se encuentra alrededor de \(75\)
kg, siendo el estrato \(4\) el que presenta un mayor promedio con un
valor cercano a \(80\) kg, y el estrato \(5\) el que presenta un menor
promedio con un valor cercano a \(65\) kg. Es de anotar que el estrato
\(5\) no posee bandas de confianza debido a que dicho estrato solo
cuenta con una observación, y en consecuencia no posee medidas de
variabilidad.
Aunque hay una pequeña diferencia entre la media
de los estratos, no es posible hablar sobre que las diferencias son
significativas, ya que se tiene que las bandas de confianza de cada
estrato se traslapan unos con otros.
Gráfico de dispersión
Este gráfico se emplea para hacer cruces entre dos variables cuantitativas, las cuales pueden ser diferenciadas por una cualitativa, mediante el cambio de colores. Este sirve para ver tendencias, diferencias entre clases, relaciones entre dos variables cuantitativas, y permite apreciar donde se centra el total de observaciones dados dos atributos cuantitativos. Este gráfico puede ser realizado mediante la función plot() de la librería graphics de R.
Para diferenciar los colores usados en el gráfico, es posible establecerse las categorías mediante la función legend() de la librería graphics de la base de R.
Gráfico de dispersión por categorías
plot(x = datos$Edad, y = datos$Altura, xlab = "Edad (años)", ylab = "Altura (m)",
main = "Edad vs Altura", pch = 19, col = datos$DeporFavorito)
legend("bottomright", legend = levels(datos$DeporFavorito), col = 1:4, pch = 19)
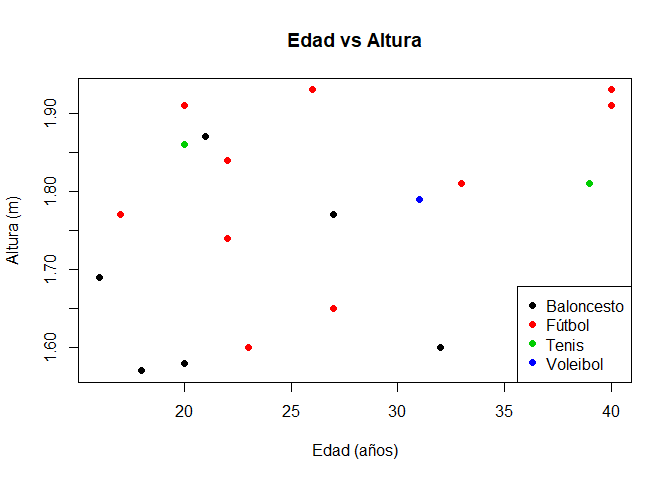
Interpretación
En el gráfico de dispersión anterior, se muestran un cruce entre la
Altura y la Edad de las personas encuestadas, estableciendo categorías
por los deporte favorito de las personas. En este gráfico no se observa
ninguna tendencia para ninguno de los deportes de evaluados, en donde,
especial atención debe tenerse con Tenis y Voleibol debido a que el
primer deporte posee solo dos puntos, mientras que el segundo deporte
posee un solo punto, así que no tiene mucho sentido hablar de tendencias
en estos dos casos.
Adicionalmente en dicho gráfico, no es
posible hablar de observaciones atípicas o datos atípicos, pues no se
evidencian puntos que se encuentren por fuera de los límites normales de
Peso o Edad de una persona. Tampoco es posible hablar de una
conglomeración de datos debido la alta dispersión que se ve entre los
puntos.
Referencias
Chambers, J., Cleveland, W., Kleiner, B., & Tukey, P. (1983). Graphical methods for data analysis (1st ed.). Wadsworth & Brooks/Cole.
Hernández, F., & Correa, J. (2018). Gráficos con r. Universidad Nacional de Colombia.
McGill, R., Tukey, J., & Larsen, W. (1978). Variations of box plots. The American Statistician, 32(1), 12–16.