Medidas estadísticas
Caso de estudio
Suponga que se está interesado en observar la evolución en el desempeño
que tuvo un grupo de $10$ estudiantes en el curso de Estadística I.
Para ello se toma de referencia la nota obtenida en el primer y cuarto
parcial de la materia, obteniendo los siguientes resultados
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Parcial 1 | 2.7 | 4.0 | 3.1 | 2.7 | 2.9 | 1.3 | 2.6 | 2.8 | 3.3 | 2.1 |
| Parcial 4 | 1.8 | 4.7 | 3.4 | 0.7 | 4.1 | 3.6 | 4.5 | 3.2 | 3.4 | 2.0 |
Medidas de forma
Estas medidas tienen por objetivo evidenciar si el conjunto de observaciones tiene o no una forma simétrica y observar su nivel de concentración.
Coeficiente de asimetría
Este valor permite identificar si el conjunto de datos se distribuye
uniformemente alrededor de las medidas de tendencia central.
\begin{align*} \gamma_1 = \frac{1}{n}\frac{\sum_{i=1}^n{(x_i-\bar{X})^3}}{S^3} \quad \quad -\infty<\gamma_1<\infty \end{align*}
El signo de $\gamma_1$ indica la dirección de la asimetría.
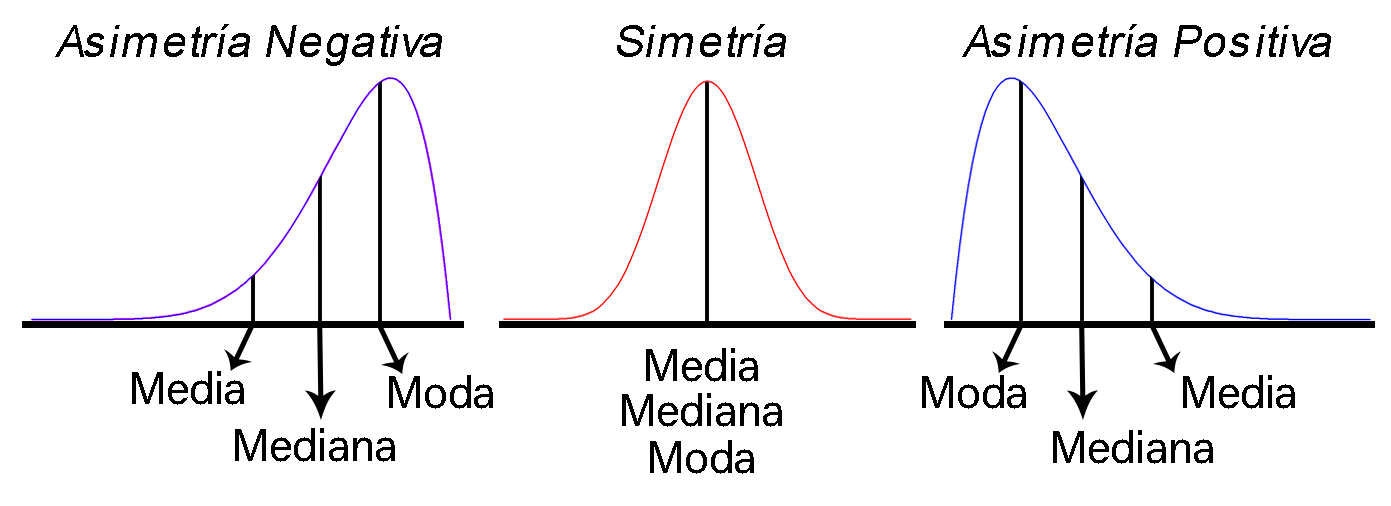
$\gamma_1>0$indica asimetría positiva, es decir, las observaciones se reúnen más en la parte izquierda de las medidas de tendencia central.$\gamma_1<0$indica asimetría negativa, es decir, las observaciones se reúnen más en la parte derecha de las medidas de tendencia central.$\gamma_1\sim0$indica simetría, es decir, existe aproximadamente la misma cantidad de observaciones a los dos lados de las medidas de tendencia central.
Representación tipos de Asimetría
Entre las funciones base del programa R no hay ninguna función
que calcule el coeficiente de asimetría de un conjunto de observaciones,
pero es posible realizar el cálculo mediante la función
skewness(datos) de la librería e1071.
Ejercicio Caso de Estudio
Calcule el coeficiente de asimetría de las notas obtenidas por los \(10\) estudiantes, en el primer y cuarto parcial del curso de Estadística I de forma manual.
Solución Manual
El coeficiente de asimetría asociado a la nota de los estudiantes del
curso de Estadística I, para los parciales \(1\) y \(4\), depende del
valor promedio \(\bar{X}\) y la desviación estándar \(S\). Por tanto al
emplear los valores ya calculados en
Clase
01 y
Clase
02 (ver Solucion manual o en R), se tendrá que el coeficiente de
asimetría para los dos parciales estará dado por
\[\begin{align*}
\gamma_{1,P_1} &= \frac{1}{10}\left[\frac{(2.7 - 2.75)^3 + (4.0 - 2.75)^3 + \ldots + (2.1 - 2.75)^3}{0.7121954^3}\right] \\
&= -0.3213918 \\
\gamma_{1,P_4} &= \frac{1}{10}\left[\frac{(1.8 - 3.14)^3 + (4.7 - 3.14)^3 + \ldots + (2.0 - 3.14)^3}{1.273839^3}\right] \\
&= -0.536286
\end{align*}\] De lo anterior se observa que en ambos casos el
coeficiente de asimetría es menor que \(0\), lo cual significa que las
notas obtenidas en los dos parciales posee una asimetría negativa, es
decir, las notas obtenidas por los estudiantes se encuentran agrupadas
en la parte derecha, y en consecuencia, se tiene que algunos (pocos)
estudiantes obtuvieros notas muy bajaras, respecto al resto de sus
compañeros.
También puede corroborarse el comportamiento asimétrico negativo, al
observar los valores obtenidos por la media y la mediana, en donde para
ambos parciales, se aprecia que la media posee un valor más bajo que la
mediana.
Ejercicio Caso de Estudio
Calcule el coeficiente de asimetría de las notas obtenidas por los \(10\) estudiantes, en el primer y cuarto parcial del curso de Estadística I en R.
Solución en R
Para realizar el cálculo del coeficiente de asimetría, para la nota
obtenida por los estudiantes de Estadística I en los los parciales \(1\)
y \(4\), se emplea la función skewness() de la librería
e1071 de R, tal que
## Si no se tiene instalada la librería e1071, puede instalarse mediante
# install.packages('e1071', dependencies = T)
# Se carga la librería para el cálculo de la asimetría
library(e1071)
## Se calcula el coeficiente de asimetría de cada conjunto de datos
# Coeficiente de asimetría Parcial 1
skewness(P1)
[1] -0.3213918
# Coeficiente de asimetría Parcial 4
skewness(P4)
[1] -0.536286
Coeficiente de exceso de curtosis
Este valor permite observar el grado de concentración del conjunto de
datos
\begin{align*} \gamma_2 = \frac{1}{n}\frac{\sum_{i=1}^n{(x_i-\bar{X})^4}}{S^4}-3 \quad \quad -2<\gamma_2<\infty \end{align*}
El signo de $\gamma_2$ indica el nivel de concentración.
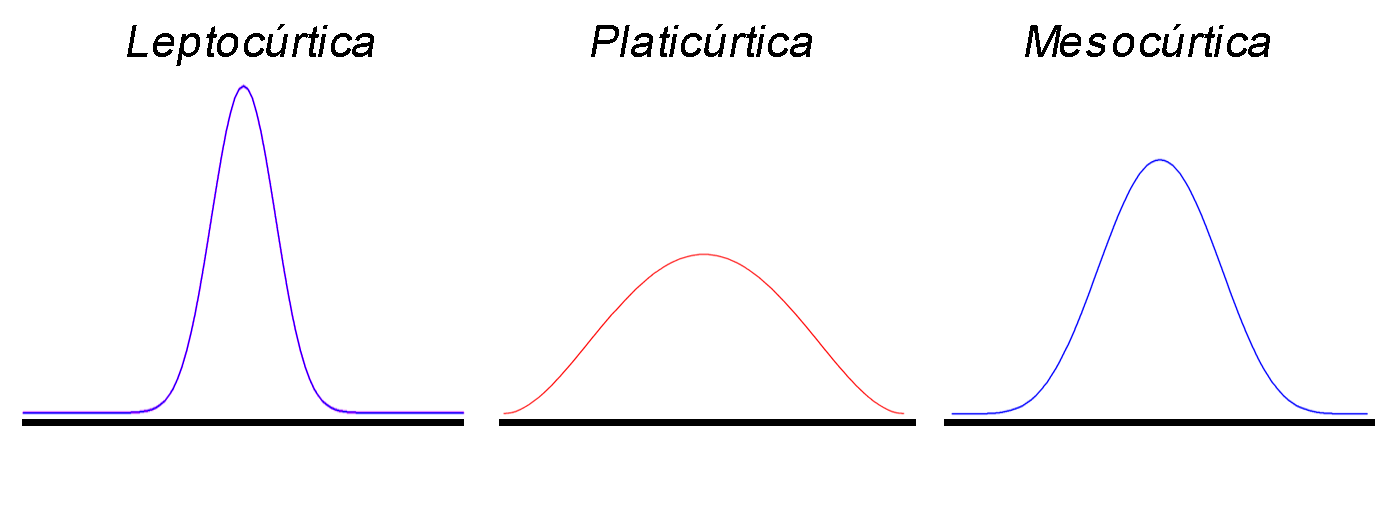
$\gamma_2>0$indica leptocurtosis, es decir, la forma de los datos es más en punta y posee colas menos anchas.$\gamma_2<0$indica platicurtosis, es decir, la forma de los datos es más plana y posee colas más anchas.$\gamma_2\sim0$indica mesocurtosis, es decir, tanto la punta como las colas son similares a la distribución normal.
Representación tipos de kurtosis
Entre las funciones base del programa R no hay ninguna función
que calcule el coeficiente de exceso de curtosis de un conjunto de
observaciones, pero es posible realizar el cálculo mediante la función
kurtosis(datos) de la librería e1071.
Ejercicio Caso de Estudio
Calcule el coeficiente de exceso de curtosis de las notas obtenidas por los \(10\) estudiantes, en el primer y cuarto parcial del curso de Estadística I, de forma manual.
Solución Manual
Similar al coeficiente de asimetría, el coeficiente de exceso de curtosis depende del valor promedio \(\bar{X}\) y la desviación estándar \(S\), de los parciales \(1\) y \(4\) del curso de Estadística I. Por tanto al emplear los valores ya calculados en Clase 01 y Clase 02 (ver Solucion manual o en R), se tendrá que el coeficiente de exceso de curtosis para los dos parciales estará dado por \[\begin{align*} \gamma_{2,P_1} &= \frac{1}{10}\left[\frac{(2.7 - 2.75)^4 + (4.0 - 2.75)^4 + \ldots + (2.1 - 2.75)^4}{0.7121954^4}\right] - 3 \\ &= -0.2216579 \\ \gamma_{2,P_4} &= \frac{1}{10}\left[\frac{(1.8 - 3.14)^4 + (4.7 - 3.14)^4 + \ldots + (2.0 - 3.14)^4}{1.273839^4}\right] - 3 \\ &= -1.078075 \end{align*}\] A partir de los valores calculados, se observa que en ambos casos, los coeficientes de exceso de curtoris es menor que \(0\), y por tanto, se puede concluir que las notas de los estudiantes posee un comportamiento platicúrtico, es decir, las notas obtenidas por los estudiantes en el curso de Estadística I, poseen un comportamiento relativamente uniforme, debido a que su comportamiento es muy plano.
Ejercicio Caso de Estudio
Calcule el coeficiente de exceso de curtosis de las notas obtenidas por los \(10\) estudiantes, en el primer y cuarto parcial del curso de Estadística I en R.
Solución en R
Para realizar el cálculo del coeficiente de exceso de curtosis, para la
nota obtenida por los estudiantes de Estadística I en los los parciales
\(1\) y \(4\), se emplea la función kurtosis() de la
librería e1071 de R, tal que
## Se calcula el coeficiente de exceso de curtosis de cada conjunto de datos
# Coeficiente de exceso de curtosis Parcial 1
kurtosis(P1)
[1] -0.2216579
# Coeficiente de exceso de curtosis Parcial 4
kurtosis(P4)
[1] -1.078075
Medidas de asociación
Estas medidas tienen por objetivo estimar la magnitud con la que dos
fenómenos se relacionan, en donde, entre mayor sean estas medidas, mayor
será el grado de asociación que tendrán las variables. Si se define
$x_1, x_2, \ldots, x_n$ y $y_1, y_2, \ldots, y_n$ como dos conjuntos
de $n$ observaciones, entonces
Covarianza
Mide si existe o no dependencia lineal entre las variables, e indica el
grado de variación conjunta de dos variables respecto a sus medias
\begin{align*} S_{xy} = \frac{1}{n}\sum_{i=1}^n{(x_i-\bar{X})(y_i-\bar{Y})} \end{align*}
El signo de $S_{xy}$ indica el tipo de dependencia lineal que hay
entre las variables.
$S_{xy} > 0$indica que hay dependencia lineal positiva entre las variables, es decir, cuando aumenta una variable, la otra también aumenta.$S_{xy} < 0$indica que hay dependencia lineal negativa entre las variables, es decir, cuando aumenta una variable, la otra disminuye.$S_{xy} \approx 0$indica que no existencia dependencia lineal entre las dos variables.
En R puede calcularse la covarianza de dos conjunto de
observaciones mediante la función cov(datos1, datos2).
Ejercicio Caso de Estudio
Calcule el covarianza que hay entre las notas obtenidas en el primer parcial y el cuarto parcial, por los \(10\) estudiantes que vieron el curso de Estadística I de forma manual.
Solución Manual
A diferencia de las anteriores medidas, el coeficiente de covarianza buscar observar si existe o no una dependencia lineal entre dos grupos de observaciones. Para ello, se emplean los valores promedio \(\bar{X}_{P1}\) y \(\bar{X}_{P4}\) obtenido en la clase Clase 01 para ambos parciales, y con éstos se busca comparar si hay una relación entre las notas obtenidas en el parcial \(1\) y el parcial \(4\), tal que \[\begin{align*} S_{P_1P_4} &= \frac{1}{10}\left[(2.7-2.75)(1.8-3.14) + \ldots + (2.1 - 2.75)(2.0 - 3.14)\right] \\ S_{P_1P_4} &= 0.2655556 \end{align*}\] Dado que del coeficiente de covarianza, solo es posible interpretar el signo o cuando el valor está muy cercano a \(0\), se concluye entonces que existe una relación lineal positiva entre la nota obtenida en el primer parcial y el cuarto parcial.
Ejercicio Caso de Estudio
Calcule el covarianza que hay entre las notas obtenidas en el primer parcial y el cuarto parcial, por los \(10\) estudiantes que vieron el curso de Estadística I en R.
Solución en R
Para calcular la covarianza de la nota obtenida por los estudiantes de
Estadística I en los los parciales \(1\) y \(4\), se emplea la función
cov() de R, tal que
# Se calcula la Covarianza entre el Parcial 1 y 4
cov(P1, P2)
[1] 0.2655556
Correlación
Mide la fuerza de la dependencia lineal que hay entre variables, esta va
entre -1 y 1
\begin{align*} \rho_{xy} = \frac{S_{xy}}{S_{x}S_{y}} \quad \quad -1<\rho_{xy}<1 \end{align*}
El valor de $\rho_{xy}$ indica el tipo y fuerza de la dependencia
lineal que hay entre las variables
$\rho_{xy} = 1$indica que existe dependencia lineal positiva exacta entre las variables, es decir, cuando aumenta una variable, la otra aumenta proporcionalmente en la misma cantidad. Este aumento es de la forma$Y = a + bX$, siendo$a$y$b$dos constantes, con$b>0$.$\rho_{xy} = -1$indica que existe dependencia lineal negativa exacta entre las variables, es decir, cuando aumenta una variable, la otra disminuye proporcionalmente en la misma cantidad. Este aumento es de la forma$Y = a + bX$con$a y b$dos constantes, y$b<0$.$\rho_{xy} = 0$No existe dependencia lineal entre las variables.
Además, se tendrá que si
$0.5 < \rho_{xy} \leq 1$fuerte correlación positiva entre$X$y$Y$.$0.3 < \rho_{xy} \leq 0.5$moderada correlación positiva entre$X$y$Y$.$0.1 < \rho_{xy} \leq 0.3$débil correlación positiva entre$X$y$Y$.$-0.1 \leq \rho_{xy} \leq 0.1$débil o ninguna correlación entre$X$y$Y$.$-0.3 \leq \rho_{xy} < -0.1$débil correlación negativa entre$X$y$Y$.$-0.5 \leq \rho_{xy} < -0.3$moderada correlación negativa entre$X$y$Y$.$-1 \leq \rho_{xy} < -0.5$fuerte correlación negativa entre$X$y$Y$.
En R puede calcularse la correlación de dos conjunto de
observaciones mediante la función cor(datos1, datos2).
Ejercicio Caso de Estudio
Calcule la correlación que hay entre las notas obtenidas en el primer parcial y el cuarto parcial, por los \(10\) estudiantes que vieron el curso de Estadística I de forma manual.
Solución Manual
Similar al coeficiente de covarianza, el coeficiente de correlación buscar si existe o no una dependencia lineal entre dos grupos de observaciones, pero a diferencia de éste, el coeficiente de correlación muestra la fuerza de dicha relación. Por tanto, para realizar el cálculo de la correlación entre los parciales \(1\) y \(4\), se emplea el coeficiente de covarianza y las desviaciones estándar calculadas anteriormente en esta misma clase, tal que \[\begin{align*} \rho_{xy} = \frac{0.2655556}{(0.7121954)(1.273839)} = 0.2927127 \end{align*}\] Del resultado anterior se concluye, que hay existe una correlación débil entre las notas obtenidas por los estudiantes en el parcial \(1\) y el parcial \(4\), del curso de Estadística 1.
Ejercicio Caso de Estudio
Calcule la correlación que hay entre las notas obtenidas en el primer parcial y el cuarto parcial, por los \(10\) estudiantes que vieron el curso de Estadística I en R.
Solución en R
Para calcular la correlación de la nota obtenida por los estudiantes de
Estadística I en los los parciales \(1\) y \(4\), se emplea la función
cor() del programa R, tal que
# Se calcula la Correlación entre el Parcial 1 y 4
cor(P1, P2)
[1] 0.2927127