print('hello')
hello
Introducción a modelos SARIMA
Existen situaciones en las que es posible enfrentarse a series temporales que poseen entre sus componentes, un comportamiento estacional, lo cual hace que tanto la media como otras estadísticas dadas en un periodo no sean estacionarias a lo largo del tiempo. Y a causa de ello, se tendrá que los métodos de modelación presentados hasta el momento no resulten ser apropiados para el ajuste del conjunto de observaciones asociados a la serie de interés.
La componente estacional de una serie temporal se ha definido hasta ahora como fluctuaciones que se repiten anualmente o en periodos que poseen duración menor a un año, las cuales se encuentran relacionadas con fenómenos económicos, ambientales o sociales, que hacen que el comportamiento de la serie tome un comportamiento repetitivo a través de los años.
La periodicidad de la componente estacional es usualmente denotada por
la letra $s$, y define la longitud o número de periodos en los cuales
se observa que se repite el comportamiento de la serie. Ahora bien, dado
que la estacionalidad es una señal de que la serie de tiempo no es
estacionaria, es necesario eliminar dicha componente con el fin de
poder modelar ésta, de la forma como se ha venido trabajando hasta el
momento.
Ejemplo serie estacional
Suponga que la siguiente serie temporal está dada por la producción mensual de juguetes para niños (en millones), de una empresa ubicada en el municipio de Itagüi, para el periodo marzo de 1995 hasta febrero de 2004.
library(plotly)
library(sarima)
set.seed(127102)
Serie1 <- sim_sarima(n = 108, model = list(ar = c(-0.89, -0.9), ma = 0.5, sar = c(0.2,
0.15), sma = 0, sigma2 = 50, nseasons = 12, iorder = 0, siorder = 1), xintercept = 0,
n.start = 1050) + 250
Serie1 <- ts(Serie1, start = c(1995, 3), frequency = 12)
fechas1 <- time(Serie1)
## Gráfico Básico
plot.ts(Serie1, main = "Producción mensual de juguetes", ylab = "Producción mensual")
## Gráfico Avanzado
plot_ly(x = ~fechas1, y = ~Serie1, mode = "lines", text = paste("Valor =", round(Serie1,
3)), width = 700, height = 400, type = "scatter") %>% layout(title = "Producción mensual de juguetes",
xaxis = list(title = "Mes"), yaxis = list(title = "Producción mensual")) %>%
layout(margin = list(l = 60, r = 30, b = 60, t = 60, pad = 4))
Operador de diferencia estacional
Con tal propósito en mente, suponga una serie $Y_t$ la cual posee
una componente estacional con periodicidad $s$, entonces con el fin
de eliminar dicha componente de la serie temporal, será necesaria
diferenciar la serie temporal con respecto a la serie rezagada $s$
periodos en el tiempo. Éste procedimiento es conocido como
diferencia estacional y se define como
\begin{align*} \Delta_s Y_t = Y_t - Y_{t-s} \end{align*}
siendo $\Delta_s = (1-L^s)$. Note que $\Delta_s \neq \Delta^s$,
pues $\Delta^s = (1-L)^s$ representa el operador de diferencias
presentado en la Clase
11.
En general, el operador de diferencias estacionales de periodo $s$ se
define como \begin{align*} \Delta_s^D = (1-L^s)^D \end{align*}
Siendo $D$ el parámetro que indica el número de diferencias
estacionales.
Modelos autorregresivos integrados de media móvil estacionales (SARIMA)
Se dice que una serie de tiempo $Y_t$ posee una estructura
$SARIMA(p,d,q)(P,D,Q)[S]$ si se cumple que
\begin{align*} \Phi_{P} (L^s) \; \Phi_p (L)\; \Delta^D_s \; \Delta^d \; Y_t = \Theta_{Q} (L^s)\; \Theta_q (L) \;\varepsilon_t \end{align*}
con $\varepsilon_t \sim RB(0, \sigma_{\varepsilon}^2)$, donde
\begin{align*} \Phi_p(z) = 1 - \sum_{j=1}^p\phi_j z^j \\ \Theta_q(z) = 1 + \sum_{j=1}^q\theta_j z^j \end{align*}
son los polinomios de rezagos autorregresivos y de medias móviles,
regulares, respectivamente, cada una sin raíces unitarias y con módulo
mayor a 1, y
\begin{align*} \Phi_{P}(z^s) = 1 - \sum_{j=1}^{P}\phi_{s,j} z^{js} \\ \Theta_{Q}(z^s) = 1 + \sum_{j=1}^{Q}\theta_{s,j} z^{js} \end{align*}
son los polinomios de rezagos autorregresivos y de medias móviles,
estacionales, respectivamente, sin raíces unitarias y con módulo mayor
a 1. Además, $L$ el operador de rezagos,
\begin{align*} \Delta^d=(1-L)^d \end{align*} es el operador de
diferencias regulares y
\begin{align*} \Delta^D_s=(1-L^s)^D \end{align*}
es el operador de diferencias estacionales.
Identificación de un modelo SARIMA(p,d,q)(P,D,Q)[S]
Ahora bien, con el fin de identificar los órdenes regulares $p$,
$d$, $q$, y estacionales $P$, $D$ y $Q$ asociados a un modelo
$SARIMA(p,d,q)(P,D,Q)[S]$, es necesario realiza los siguientes
procedimientos
- Identificar el órden de integración regular
$d$y estacional$D$que posee la serie temporal, mediante el análisis de raíces unitaria, con el fin de obtener una serie estacionaria en covarianza. - Identificar el órden autorregresivo regular
$p$y estacional$P$, al igual que el órden de media móvil regular$q$y estacional$Q$que posee la serie temporal, mediante análisis gráficos y estadístico de la serie, o serie diferenciada dependiendo de los hallazgos del punto anterior.
Análisis de raices unitarias
Con el fin de observar si la serie temporal posee o no raíces unitarias regulares o estacionales, se recomienda inicialmente la aplicación de pruebas para raíces unitarias estacionales, esto debido a que hay situaciones en las cuales, puede ocurrir que una serie temporal presente que tiene ambos tipos de raíces, pero que, al eliminar aquellas raíces unitarias estacionales mediante diferenciación estacional, se obtiene a su vez la eliminación de las raíces unitarias.
Por ello, se inicia con la aplicación de la prueba para raíces unitarias
estacionales Osborn, Chui, Smith, and Birchenhall (OCSB), la cual puede
realizarse en R, mediante la función ocsb.test() de la
librería forecast.
Dicha prueba busca probar la hipótesis
\begin{align*} H_0: Y_t \text{ posee raíces unitarias estacionales} \\H_1: Y_t \text{ no posee raíces unitarias estacionales} \end{align*}
En donde, para rechazar la hipótesis nula, se tendrá que el
estadístico de prueba deberá ser menor al valór de la región crítica
calculado a un $5\%$ de significancia.
library(forecast)
ocsb.test(Serie1)
OCSB test
data: Serie1
Test statistic: -0.9148, 5% critical value: -1.803
alternative hypothesis: stationary
Lag order 0 was selected using fixed
De la prueba anterior, se encuentra que el estadístico de prueba posee
un valor de $-0.9148$, mientras que el valor crítico de la región
crítica calculado a un nivel de significancia del $5\%$ es de
$-1.803$.
Por tanto, se concluye que la serie temporal posee una raíz unitaria
estacional, esto es, $D=1$. Con el fin de observar si es necesario
realizar otra diferenciación estacional y o diferenciaciones regulares,
será necesario aplicar una diferenciación estacional de orden $s=12$
(serie mensual), para así poder eliminar la raíz unitaria estacionaria
encontrada y poder realizar nuevamente la prueba OCSB en el caso de
raíces unitarias estacionales o la prueba Dickey-Fuller Aumentada (ADF)
en el caso de raíces unitarias regulares.
Para realizar la eliminación de la raíz unitaria estacional encontrada
anteriormente, se emplea la función diff() con argumento lag = 12,
seguido de la aplicación de la prueba OCSB, para observar si existen
todavía raíces unitarias estacionales.
dSerie1 <- diff(Serie1, lag = 12)
ocsb.test(dSerie1)
OCSB test
data: dSerie1
Test statistic: -7.1908, 5% critical value: -1.803
alternative hypothesis: stationary
Lag order 0 was selected using fixed
Al realizar nuevamente la prueba se encuentra que el valor del
estadístico de prueba $-7.1908$ se encuentra por debajo del valor
crítico $-1.803$, y por tanto se concluye a un nivel de significancia
del $5\%$ que se rechaza la hipótesis nula, a favor de la alternativa,
es decir, se rechaza la existencia de más raíces unitarias estacionales.
Dado que no se encontraron raíces unitarias estacionales, se procede a
realizar la prueba ADF, mediante la función adf.test() de la librería
tseries.
Dicha prueba busca probar la hipótesis
\begin{align*} H_0: Y_t \text{ posee raíces unitarias regulares} \\H_1: Y_t \text{ no posee raíces unitarias regulares} \end{align*}
En donde, para rechazar la hipótesis nula, será necesario que el
P-valor obtenido por la prueba sea menor al $5\%$, el cual es el nivel
de significancia que estamos empleando para las pruebas.
library(tseries)
adf.test(dSerie1)
Augmented Dickey-Fuller Test
data: dSerie1
Dickey-Fuller = -5.9194, Lag order = 4, p-value = 0.01
alternative hypothesis: stationary
De la prueba Dickey-Fuller Aumentada, se aprecia que el P-valor es igual
a $0.01$ o menor (debido a la advertencia que obtenida al aplicar la
prueba), lo cual indica que hay evidencia suficiente para rechazar
$H_0$ a favor de la alternativa, esto es, concluir que no la serie
diferenciada no posee raíces regulares.
En conclusión a lo obtenido en esa sección, se tendrá que la serie
empleada, posee un orden de diferenciación regular $d=0$ y un órden de
diferenciación estacional $D=1$
Identificación de órdenes p, q, P y Q
Para facilitar la identificación de los órdenes regulares y estacionales
$(p, q)$ y $(P, Q)$, respectivamente, se aconseja el empleo de la
serie obtenida de diferencias obtenida en la sección anterior, ésto
debido a que, al eliminar las raíces unitarias que posee la serie
temporal, se obtiene una serie estacionaria en covarianza, lo cual
permite que puedan emplearse los mismos procedimientos explicados en
modelos ARMA, para identificar los órdenes $p$ y $q$, solo en en
esta situación, será necesario observar si existen o no rezagos
estacionales significativos.
ACF y PACF para la identificación de los órdenes p, q, P y Q
Un método clásico para la identificación es el de realizar los gráficos de la ACF y PACF de la serie (o serie diferenciada si fue necesario realizar este procedimiento), para tratar de identificar los órdenes regulares y estacionales que posee la serie temporal.
Para ello se emplea las funciones acf() y pacf(), con el argumento
lag.max = 30, ésto con el objetivo de poder visualizar al menos dos
periodos estacionales, ya que tenemos que la periodicidad de la serie
$s=12$.
# Gráfico básico
par(mfrow = c(1, 2))
acf(dSerie1, main = "ACF Producción de juguetes", lag.max = 30)
pacf(dSerie1, main = "PACF Producción de juguetes", lag.max = 30)
# Gráfico avanzado
library(feasts)
library(tsibble)
dSerie1ts <- as_tsibble(dSerie1)
acfSerie1 <- dSerie1ts %>% ACF(value, lag_max = 30) # Calcula valores de ACF
pacfSerie1 <- dSerie1ts %>% PACF(value, lag_max = 30) # Calcula valores de PACF
CI <- function(x) qnorm((1 + 0.95)/2)/sqrt(sum(!is.na(x))) # Crea función para
plotacf <- plot_ly(acfSerie1, width = 700, height = 400) %>% layout(title = "ACF",
xaxis = list(title = "Lags"), yaxis = list(title = "ACF")) %>% add_bars(x = ~1:nrow(acfSerie1),
y = ~acfSerie1$acf, width = 0.2, text = paste("ACF =", acfSerie1$acf)) %>%
layout(shapes = list(list(type = "line", x0 = 0, x1 = nrow(acfSerie1), y0 = CI(dSerie1ts$value),
y1 = CI(dSerie1ts$value), line = list(dash = "dot")), list(type = "line",
x0 = 0, x1 = nrow(acfSerie1), y0 = -CI(dSerie1ts$value), y1 = -CI(dSerie1ts$value),
line = list(dash = "dot")))) %>% layout(margin = list(l = 60, r = 30,
b = 60, t = 60, pad = 4))
plotpacf <- plot_ly(pacfSerie1, width = 700, height = 400) %>% layout(title = "PACF",
xaxis = list(title = "Lags"), yaxis = list(title = "PACF")) %>% add_bars(x = ~1:nrow(pacfSerie1),
y = ~pacfSerie1$pacf, width = 0.2, text = paste("PACF =", pacfSerie1$pacf)) %>%
layout(shapes = list(list(type = "line", x0 = 0, x1 = nrow(pacfSerie1),
y0 = CI(dSerie1ts$value), y1 = CI(dSerie1ts$value), line = list(dash = "dot")),
list(type = "line", x0 = 0, x1 = nrow(pacfSerie1), y0 = -CI(dSerie1ts$value),
y1 = -CI(dSerie1ts$value), line = list(dash = "dot")))) %>% layout(margin = list(l = 60,
r = 30, b = 60, t = 60, pad = 4))
subplot(plotacf, plotpacf, nrows = 1, margin = 0.08) %>% layout(title = "ACF y PACF Producción de juguetes",
yaxis = list(title = "ACF"), yaxis2 = list(title = "PACF"), xaxis2 = list(title = "Lags"),
margin = list(r = 30, l = 60, t = 60, b = 60, pad = 4), height = 400, showlegend = FALSE)
En los gráfico anterior, se aprecia que en la ACF hay un decaimiento
lento a cero, de sus autocorrelaciones, en donde, se evidencia un
comportamiento sinusoidal en su decaimiento. También se aprecia que
entre los rezagos significativos estacionales, solo se encuentra el
primer rezago estacional (reazago 12) como significativo. Por tanto, no
hay evidecia alguna, sobre que la serie temporal de interés, posea
órdenes $q$ o $Q$ mayores a 1.
Por su parte, en la PACF se aprecia un decaimiento rápido a cero de las
autocorrelaciones parciales, en donde, es posible observar que los dos
rezagos se encuentran por fuera de las bandas de confianza, por lo cual
se tendrá evidencia sobre que el el órden $p$ podría ser igual a
$2$. Además, no se presenta ningún rezago estacional significativo, ya
que tanto el rezago número $12$ como el razago número $24$ no
resultan ser significativos, lo cual es evidencia sobre que el órden
estacional $P$ de la serie de interés no es mayor a $1$.
Función de autocorrelación extendida (EACF)
Una alternativa propuesta por Tsay and Tiao (1984), para la identificación de un modelo ARMA, es mediante la función de autocorrelación extendida, la cual posee un desempeño relativamente bueno, cuando el tamaño de la serie de tiempo es grande. Esta función usa el hecho de que si la parte AR de un ARMA fuese conocida, entonces al filtrar de la serie esta componente mediante regresión, se obtendría un proceso MA puro con la propiedad de patrón de corte en su ACF.
Teóricamente, los órdenes p,q del modelo ARMA tendrán un comportamiento de tríangulo de ceros (ordenes viables) lo cuál indicará los órdenes del proceso ARMA. Es de anotar que dicho comportamiento pocas veces ocurre en la práctica.
Representación de tabla EACF para modelo ARMA(1,1)
| AR | 0 | 1 | 2 | 3 | \(\vdots\) |
|---|---|---|---|---|---|
| 0 | \(X\) | \(X\) | \(X\) | \(X\) | \(\vdots\) |
| 1 | \(X\) | 0 | 0 | 0 | \(\vdots\) |
| 2 | \(X\) | \(X\) | 0 | 0 | \(\vdots\) |
| 3 | \(X\) | \(X\) | \(X\) | 0 | \(\vdots\) |
| \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ddots\) |
Se procede entonces a realizar la estimación de la EACF, la serie de
datos de producción mensual de juguetes para niños. Para realizar la
estimación de la EACF en R se emplean la función eacf() de la
librería TSA. Es de anotar que este método no es muy útil para
observar comportamiento estacional.
library(TSA)
eacf(dSerie1)
AR/MA
0 1 2 3 4 5 6 7 8 9 10 11 12 13
0 x x x x x x o x x o x x o x
1 x x x x x x o x x o x x o x
2 o o o o o o o o x o o x o o
3 x o o o o o o o x o o x o o
4 o x o o o o o o x o o x o o
5 o o x o o o o o o o o x o o
6 x o o x o o o o o o o x o o
7 x o o o o o o o o o o x o o
Aunque esto normalmente no ocurre, en este caso se logra apreciar en el
gráfico de la EACF, un tríangulo que apunta al órden $(p = 2, q = 0)$
lo cual es consistente con lo encontrado en los gráficos ACF y PACF.
Análisis gráfico para subconjuntos de modelos a partir del BIC
Otra alternativa propuesta para la identificación de un modelo adecuado,
es mediante la minimización de los criterios de información. En éste
caso, la función armasubsets() de la librería TSA permite realizar
un gráfico que precisa cuáles son las combinaciones de órdenes
$p, q, P$ y $Q$ que mínimizan el Críterio de Información Bayesiano
(BIC).
Se realiza entonces la estimación del gráfico, aplicando los argumentos
nar = 25 y nma = 25 para tener encuenta al menos dos periodos
estacionales en la estimación. Además, se debe emplear el argumento
really.big = T debido a que el total de rezagos que se va a estimar es
muy grande y se requiere de este argumento para poder realizar la
estimación.
plot(armasubsets(dSerie1, nar = 25, nma = 25, really.big = T))
Reordering variables and trying again:
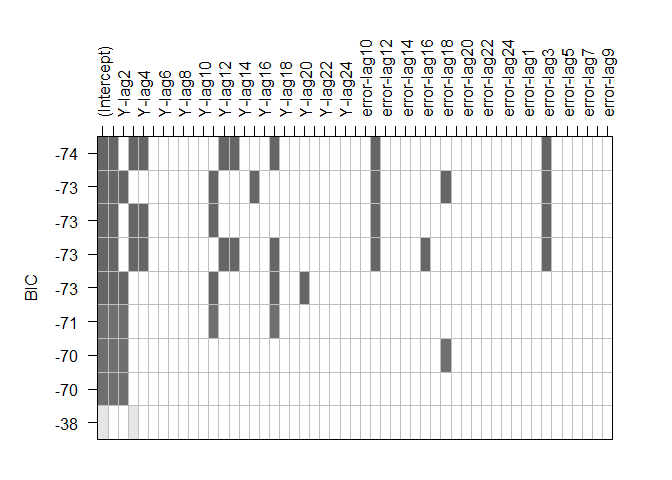
Del gráfico anterior se aprecia que entre los órdenes que resultan ser
significativos en las estimaciones, se encuentran los órdenes $3, 11$
y $18$ en la parte de médias moviles y los rezagos,
$1,2,3,4 11, 12, 13, 15, 17$ y $20$ en la parte autorregresiva. De
lo anterior, se aprecia que existen diferentes combinanciones de
modelos, siento el que minimiza el BIC un $ARMA(17, 10)$, en donde si
tenemos la parte de diferenciación que ya hicimos tendríamos un modelo
$SARIMA(17, 0, 10)(0, 1, 0)[12]$.
Aunque el modelo parece ser el que mínimiza el críterio de información
bayesiano, dicho modelo posee órdenes extremadamente grandes, entonces,
si se tiene en cuenta el órden de estacionalidad $12$ y el órden
regular $3 o 4$ de la parte autorregresiva, podría pensarse en modelos
alternativos de la forma $SARIMA(4, 0, 10)(1, 1, 0)[12]$,
$SARIMA(3, 0, 10)(1, 1, 0)[12]$, $SARIMA(4, 0, 3)(1, 1, 0)[12]$,
$SARIMA(3, 0, 3)(1, 1, 0)[12]$, entre otros.
Función auto.arima
Otra metodología usualmente empleada en la práctica es la identificación
del modelo SARIMA, mediante de la función auto.arima de la librería
forecast. Para dicha función es posible ingresar la serie en
diferencias o la serie original, pues ésta tiene la capacidad de
identificar la también el número de diferencias necesarias para hacer la
serie estacionaria.
Para la aplicación de la función auto.arima se recomienda emplear el
argumento ic = "bic", ya que por defecto emplea el críterio de
información de Akaike, el cual suele tener un mejor desempeño, solo
cuando se tengan modelos tipo $MA(\infty)$ o $AR(\infty)$.
Para la serie en diferencias se tendrá que
auto.arima(dSerie1, ic = "bic")
Series: dSerie1
ARIMA(3,0,1)(1,0,0)[12] with zero mean
Coefficients:
ar1 ar2 ar3 ma1 sar1
-1.3072 -1.2661 -0.4272 0.8157 0.4149
s.e. 0.1338 0.1232 0.1295 0.0779 0.0997
sigma^2 estimated as 44.14: log likelihood=-318.54
AIC=649.07 AICc=650.02 BIC=664.46
mientras que para la serie original se tendrá que
auto.arima(Serie1, ic = "bic")
Series: Serie1
ARIMA(3,0,1)(1,1,0)[12]
Coefficients:
ar1 ar2 ar3 ma1 sar1
-1.3072 -1.2661 -0.4272 0.8157 0.4149
s.e. 0.1338 0.1232 0.1295 0.0779 0.0997
sigma^2 estimated as 44.15: log likelihood=-318.54
AIC=649.07 AICc=650.02 BIC=664.46
De la estimación anterior se oserva por ambos métodos (empleando la
serie original o la serie en diferencias) que el modelos más apropiados
para ajustar la serie es un $SARIMA(3,0,1)(1,1,0)[12]$.
Ajuste del modelo SARIMA(p,d,q)(P,D,Q)[S]
Para realizar el ajuste de los modelos seleccionados, existen diferentes
funciones en R entre las cuales, se emplea convencionalmente la
función arima() de la librería stats y la función Arima() de la
librería forecast, las cuales arrojan información similar sobre las
estimaciones.
Ejemplo estimación modelo SARIMA(4, 0, 3)(1, 1, 0)[12] Vamos a
mostrar como se realizaría la estimación de uno de los posibles modelos
identificados anteriormente, el cual fue uno de los modelos
identificados mediante el análisis gráficos de la función
armasubsets().
Para ello empleamos la función arima, empleando la serie original.
SARIMA_303_110 <- Arima(Serie1, order = c(3, 0, 3), seasonal = list(order = c(1,
1, 0), period = 12))
SARIMA_303_110
Series: Serie1
ARIMA(3,0,3)(1,1,0)[12]
Coefficients:
ar1 ar2 ar3 ma1 ma2 ma3 sar1
-0.3216 -0.4317 0.3956 -0.2125 -0.4089 0.2944 0.4435
s.e. 0.3341 0.2767 0.2771 0.3344 0.1267 0.1721 0.0985
sigma^2 estimated as 44.29: log likelihood=-317.85
AIC=651.7 AICc=653.36 BIC=672.22
Significancia de los coeficientes
Es de anotar que las funciones arima y Arima, tienen la limiación de
que no presentan necesario mencionadas usualmen tienen la limitación de
que no presentan la significancia de los coeficientes ajustados, y por
tanto, debe ser calculadas de forma manual.
Y para ello, es necesario calcular los siguientes estadísticos de prueba
$t$ de student, definidos como
\begin{align*} t_c = \frac{\hat{\theta}_i}{\sqrt{Var(\hat{\theta}_i)}} = \frac{\hat{\theta}_i}{se(\hat{\theta}_i)} \end{align*}
Para el caso de los coeficientes autorregresivos, y
\begin{align*} t_c = \frac{\hat{\phi}_j}{\sqrt{Var(\hat{\phi}_j)}} = \frac{\hat{\phi}_j}{se(\hat{\phi}_j)} \end{align*}
para el caso de los coeficientes de media móvil.
Con éstos se busca probar los siguientes juegos de hipótesis
\begin{align*} H_0: \theta_i = 0 & & \text{vs} & & H_1: \theta_i \neq 0 \\ H_0: \phi_j = 0 & & \text{vs} & & H_1: \phi_j \neq 0 \end{align*}
donde $\theta_i$ son los parámetros de la parte autorregresiva, con
$i=0,1,\ldots,p$, y $\phi_j$ son los parámetros de la parte de media
móvil, con $j=0,1,\ldots,q$.
Además, la región crítica o región de rechazo que llevan al rechazo del
estadístico de prueba está dado por
\begin{align*} RC:\{T|T<-t_{\frac{\alpha}{2}, n-d-s*D-k} \text{ o } T>t_{\frac{\alpha}{2}, n-d-s*D-k}\} \end{align*}
con $k$ el número de parámetros en el modelo, $s$ la periodicidad de
la serie, $d$ el número de diferenciaciones regulares, $D$ el número
de diferenciaciones estacionales y $n-d-s*D-k$ el número de grados de
libertad del modelo.
Y finalmente, el P-valor asociado a cada uno de los estadísticos de
prueba estará dado por
\begin{align*} \text{P-valor} = 2\mathbb{P}(t_{n-d-s*D-k}>|t_c|) \end{align*}
Para realizar el cálculo anterior, en R es necesario extraer tanto los coeficientes estimados como los errores estándar de los coeficientes, hacer la división, y posteriormente comparar el estadístico de prueba con la región crítica, o calcular el P-valor asociado a cada uno de los estadísticos de prueba.
tc <- SARIMA_303_110$coef/sqrt(diag(SARIMA_303_110$var.coef))
n <- length(Serie1)
d <- 0
D <- 1
s <- 12
k <- length(SARIMA_303_110$coef)
gl <- n - d - s * D - k
Pvalor <- round(2 * pt(q = abs(tc), df = gl, lower.tail = FALSE), 7)
data.frame(Coef = SARIMA_303_110$coef, SE = sqrt(diag(SARIMA_303_110$var.coef)),
Estadistico = tc, Pvalor = Pvalor)
Coef SE Estadistico Pvalor
ar1 -0.3215558 0.3341452 -0.9623236 0.3384944
ar2 -0.4316644 0.2766738 -1.5601926 0.1222634
ar3 0.3956461 0.2770890 1.4278664 0.1568300
ma1 -0.2125093 0.3344166 -0.6354629 0.5267571
ma2 -0.4089286 0.1266677 -3.2283581 0.0017440
ma3 0.2944392 0.1720911 1.7109497 0.0905738
sar1 0.4435416 0.0984754 4.5040854 0.0000202
De los resultados anteriores, se tiene entonces que solo los
coeficientes asociados a los órdenes $q=2$ y $P=1$ resultan ser
significativos, lo cual podría ser una señal de que el modelo no es
adecuado para el ajuste de la serie de datos, y que por tanto sería
bueno probar otro modelo seleccionado de la fase de identificación.
Validación de supuestos
Un aspecto importante a la hora de evaluar un modelo $SARIMA(p,q)$, es
la fase de validación de los supuestos de los modelos $SARIMA$, a
partir de los residuales obtenidos en el ajuste. La evaluación de los
supuestos incluye, pruebas de incorrelación, de normalidad y de
homocedasticidad.
El objetivo de la evaluación de los supuestos permite observar si el modelo propuesto es o no adecuado para modelar la serie de interés, ya que de no cumplirse alguno de éstos, se tendrá clara evidencia sobre que el modelo propuesto no posee la capacidad de capturar algunos patrones o comportamientos que posee la serie.
Pruebas de incorrelación
Para probar si los residuales del modelo ajustado cumplen el supuesto de
incorrelación, se debe probar el siguiente juego de hipótesis
\begin{align*} \begin{split} H_0: \rho(k) = 0 \\ H_1: \rho(k) \neq 0 \end{split} \quad \quad \text{ para todo } k=1,2,\ldots, h \end{align*}
en donde, si no se rechaza $H_0$ para todo
$h = max(k) = \left\lceil\frac{T}{4}\right\rceil$ se tendrá evidencia
para concluir que los residuales del modelo ajustado son
incorrelacionados.
Existen dos formas de probar si los residuales son incorrelacionados o
no, el primero es mediante análisis gráfico, el segundo mediante la
aplicación de pruebas estadísticas. Para el análisis gráfico se tiene la
ACF y la PACF, mientras que para pruebas estadísticas se tiene las
pruebas Box-Ljung y Box-Pierce, las cuales pueden realizarse mediante la
función Box-test de la librería stats con el argumento
type = "Ljung-Box" y type = "Box-Pierce", respectivamente.
# Se extraen residuales
res <- resid(SARIMA_303_110)
# Gráfico básico
par(mfrow = c(1, 2))
acf(res, main = "ACF Residuales SARIMA(3,0,3)(1,1,0)[12]", lag.max = 30)
pacf(res, main = "PACF Residuales SARIMA(3,0,3)(1,1,0)[12]", lag.max = 30)
# Gráfico avanzado
rests <- as_tsibble(res)
acfSerie2 <- rests %>% ACF(value, lag_max = 30) # Calcula valores de ACF
pacfSerie2 <- rests %>% PACF(value, lag_max = 30) # Calcula valores de PACF
plotacfres <- plot_ly(acfSerie2, width = 700, height = 400) %>% layout(title = "ACF",
xaxis = list(title = "Lags"), yaxis = list(title = "ACF")) %>% add_bars(x = ~1:nrow(acfSerie2),
y = ~acfSerie2$acf, width = 0.2, text = paste("ACF =", acfSerie2$acf)) %>%
layout(shapes = list(list(type = "line", x0 = 0, x1 = nrow(acfSerie2), y0 = CI(rests$value),
y1 = CI(rests$value), line = list(dash = "dot")), list(type = "line",
x0 = 0, x1 = nrow(acfSerie2), y0 = -CI(rests$value), y1 = -CI(rests$value),
line = list(dash = "dot")))) %>% layout(margin = list(l = 60, r = 30,
b = 60, t = 60, pad = 4))
plotpacfres <- plot_ly(pacfSerie2, width = 700, height = 400) %>% layout(title = "PACF",
xaxis = list(title = "Lags"), yaxis = list(title = "PACF")) %>% add_bars(x = ~1:nrow(pacfSerie2),
y = ~pacfSerie2$pacf, width = 0.2, text = paste("PACF =", pacfSerie2$pacf)) %>%
layout(shapes = list(list(type = "line", x0 = 0, x1 = nrow(pacfSerie2),
y0 = CI(rests$value), y1 = CI(rests$value), line = list(dash = "dot")),
list(type = "line", x0 = 0, x1 = nrow(pacfSerie2), y0 = -CI(rests$value),
y1 = -CI(rests$value), line = list(dash = "dot")))) %>% layout(margin = list(l = 60,
r = 30, b = 60, t = 60, pad = 4))
tagList(subplot(plotacfres, plotpacfres, nrows = 1, margin = 0.08) %>% layout(title = "ACF y PACF residuales modelo SARIMA(4,0,3)",
yaxis = list(title = "ACF"), yaxis2 = list(title = "PACF"), xaxis2 = list(title = "Lags"),
margin = list(r = 30, l = 60, t = 60, b = 60, pad = 4), height = 400, showlegend = FALSE))
De los gráfcos de la ACF y PACF para los residuales, podría pensarse que los residuales son incorrelacionado, pues se aprecia que aquellos residuales que salen de las bandas de confianza se encuentran muy cercanos a ella y que la escala de medición del gráfico está muy pequeño, lo cual hace que parezca que las autocorrelaciones y autocorrelaciones parciales se alejen más de las bandas de confianza, que de lo que en realidad están.
Al aplicar el estadístico Ljung-Box tenemos el siguiente resultado
Box.test(res)
Box-Pierce test
data: res
X-squared = 0.11806, df = 1, p-value = 0.7312
Donde se aprecia que el P-valor obtenido es mayor al nivel de
significancia del $5\%$, concluyendo que no se rechaza la hipótesis
nula, y en consecuencia, se concluye que los residuales del modelo
ajustado son incorrelacionados.
Pruebas de normalidad
Para probar si los residuales del modelo ajustado cumplen el supuesto de
normalidad, es necesario probar el siguiente juego de hipótesis
\begin{align*} H_0: \varepsilon_t \sim Normal \\ H_1: \varepsilon_t \not\sim Normal \end{align*}
en donde, si no se rechaza $H_0$ se tendrá evidencia para concluir
que los residuales ajustados provienen de una distribución normal.
Similar a la prueba de incorrelación, existen dos formas de probar si
los residuales se distribuyen o no normalmente, el primero el análisis
del gráfico cuantil-cuantil (QQ-Plot), mientras que el segundo es
mediante la aplicación de pruebas estadísticas tales como, la prueba
Shapiro-Wilk, Kolmogorov-Smirnov, Kuiper, etc. Para la realización del
QQ-Plot, se emplea la función qqPlot() de la librería car, mientras
que para la prueba estadística, se emplea la función shapiro.test() de
la librería stats.
library(car)
qqPlot(res)
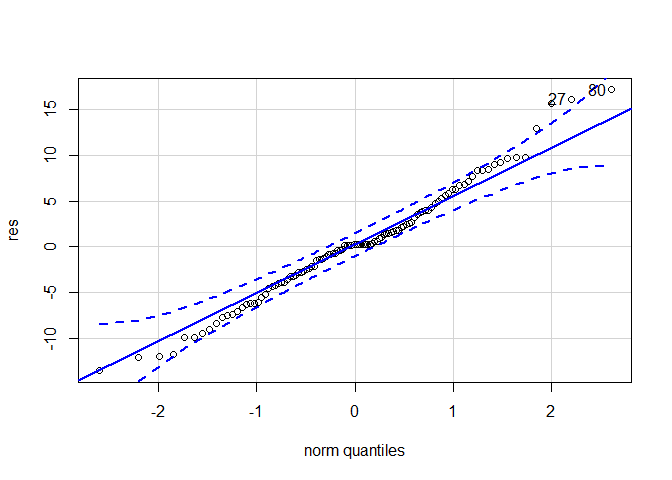
[1] 80 27
Del QQ-plot para los residuales, se aprecia que solo dos observaciones ubicadas en la parte superior izquierda se encuentran por fuera de las bandas de confianza. Pero que, al estar tan cercanas a las bandas, no es seguro que los datos no se distribuyan aproximadamente normal. Por ello se procede a aplicar la prueba Shapiro-Wilk
shapiro.test(res)
Shapiro-Wilk normality test
data: res
W = 0.9853, p-value = 0.2825
En la prueba Shapiro-Wilk se obtiene entonces un P-valor de $28.25\%$
lo cual indica que no se rechaza la hipótesis nula, y por tanto, con un
nivel de significancia del $5\%$ se asume que los residuales del
modelo estimado se distribuyen normalmente.
Pruebas de homocedasticidad
Para probar si los residuales del modelo ajustado cumplen el supuesto de
homocedasticidad, es necesario probar el siguiente juego de hipótesis
\begin{align*} \begin{split} H_0: Var(\varepsilon_t) = \sigma^2 \\ H_1: Var(\varepsilon_t) \neq \sigma^2 \end{split} \quad \quad \text{ para todo } t \end{align*}
en donde, si no se rechaza $H_0$ se tendrá evidencia para concluir
que los residuales ajustados son homocedásticos.
Similar a los dos casos anteriores, se tiene tanto análisis gráfico como
pruebas estadísticas para probar si los residuales del modelo poseen o
no variabilidad contante. Para observar si la variabilidad es constante
de forma gráfica simplemente es cuestión de realizar el gráfico de los
residuales del modelo, mientras que para la prueba estadística, se
pueden emplear la prueba Breusch-Pagan mediante la función bptest() de
la librería lmtest, o la prueba Goldfeld-Quandt mediante la función
gqtest() de la librería lmtest.
# Gráfico básico
plot.ts(res, main = "Residuales del modelo SARIMA(3,0,3)(1,1,0)[12]", ylab = "Residuales")
# Gráfico avanzado
fechas2 <- time(res)
plot_ly(x = ~fechas2, y = ~res, mode = "lines", text = paste("Valor =", round(res,
3)), width = 700, height = 400, type = "scatter") %>% layout(title = "Residuales del modelo SARIMA(3,0,3)(1,1,0)[12]",
xaxis = list(title = "Mes"), yaxis = list(title = "Residuales")) %>% layout(margin = list(l = 60,
r = 30, b = 60, t = 60, pad = 4))
Del gráfico de la serie de residuales, se aprecia que éstos se encuentran dentro de unos límites definidos, y éstos no aumentan o disminuyen con el tiempo, por lo cual podría pensarse que los residuales poseen variabilidad constante. Al realizar la prueba Breusch-Pagan se obtiene el siguiente resultado.
library(lmtest)
mres <- lm(res ~ fechas2)
bptest(mres)
studentized Breusch-Pagan test
data: mres
BP = 0.00033421, df = 1, p-value = 0.9854
De la prueba anterior, se aprecia que el P-valor asociado a la prueba
Breusch-Pagan es significativamente mayor al nivel de significancia del
$5\%$, por lo cual se asume que los residuales del modelo son
homocedásticos.
Pronóstico del modelo
Dado que el objetivo princial de trabajar con series de tiempo es poder
realizar pronósticos de la serie, se procede a calcular los mismos para
dos años en el futuro. Para ello se emplea la función forecast de la
librería forecast.
## Gráfico Básico
pred <- forecast(SARIMA_303_110)
plot(pred)
## Gráfico Avanzado
library(TSplotly)
TSplot(origin_t = 48, SARIMA_303_110, X_new, title_size = 8, ts_original = "Original time series",
ts_forecast = "Predicted time series")
Medidas de error
En caso de haber realizado validación cruzada durante la estimación del modelo, se podría realizar el cálculo de las medidas de error, para observar cuál es el modelo que mínimiza, por ejemplo, el error cuadrático medio (MSE) o el Porcentaje del error medio absoluto (MAPE).
Para ello podría emplearse la siguiente función
Med.error <- function(real, pred) {
me <- round(mean(real - pred), 4)
mpe <- round(mean((real - pred)/real) * 100, 4)
mae <- round(mean(abs(real - pred)), 4)
mape <- round(mean(abs((real - pred)/real)) * 100, 4)
mse <- round(mean((real - pred)^2), 4)
sse <- round(sum((real - pred)^2), 4)
rmse <- round(sqrt(mean((real - pred)^2)), 4)
return(data.frame(ME = me, MPE = paste0(mpe, "%"), MAE = mae, MAPE = paste0(mape,
"%"), MSE = mse, SSE = sse, RMSE = rmse))
}
Referencias
Tsay, R. S., and Tiao, G. C. (1984). Consistent estimates of autoregressive parameters and extended sample autocorrelation function for stationary and nonstationary arma models. Journal of the American Statistical Association, 79(385), 84–96.