Distribuciones de probabilidad continuas
Distribución Normal
Se dice que la variable aleatoria $X$ tiene una distribución Normal
con parámetros $\mu$ y $\sigma^2)$, si su función de densidad de
probabilidad es de la forma
\begin{align*} f(x) = \begin{cases} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x - \mu)^2}{2\sigma^2}} & -\infty<x<\infty, -\infty<\mu<\infty, \sigma^2>0 \\ 0 & \text{en otro caso} \end{cases} \end{align*}
Teorema
Si $X\sim N(\mu, \sigma^2)$, entonces se puede probar que la media y
la varianza de la variable aleatoria $X$ están dadas por
\begin{align*} \mathbb{E}(X)=\mu \quad \quad Var(X)=\sigma^2 \end{align*}
Distribución Normal estándar
Un caso particular de la distribución normal cuando la media $\mu=0$ y
ka varianza $\sigma^2=1$, recibe el nombre de distribución normal
estándar, cuya variable aleatoria se simboliza con $Z$, tal que
$Z\sim N(0,1)$, y donde su función de densidad de probabilidad está
dada por
\begin{align*} f(z) = \begin{cases} \frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}} & -\infty<z<\infty \\ 0 & \text{en otro caso} \end{cases} \end{align*}
Teorema de Estandarización
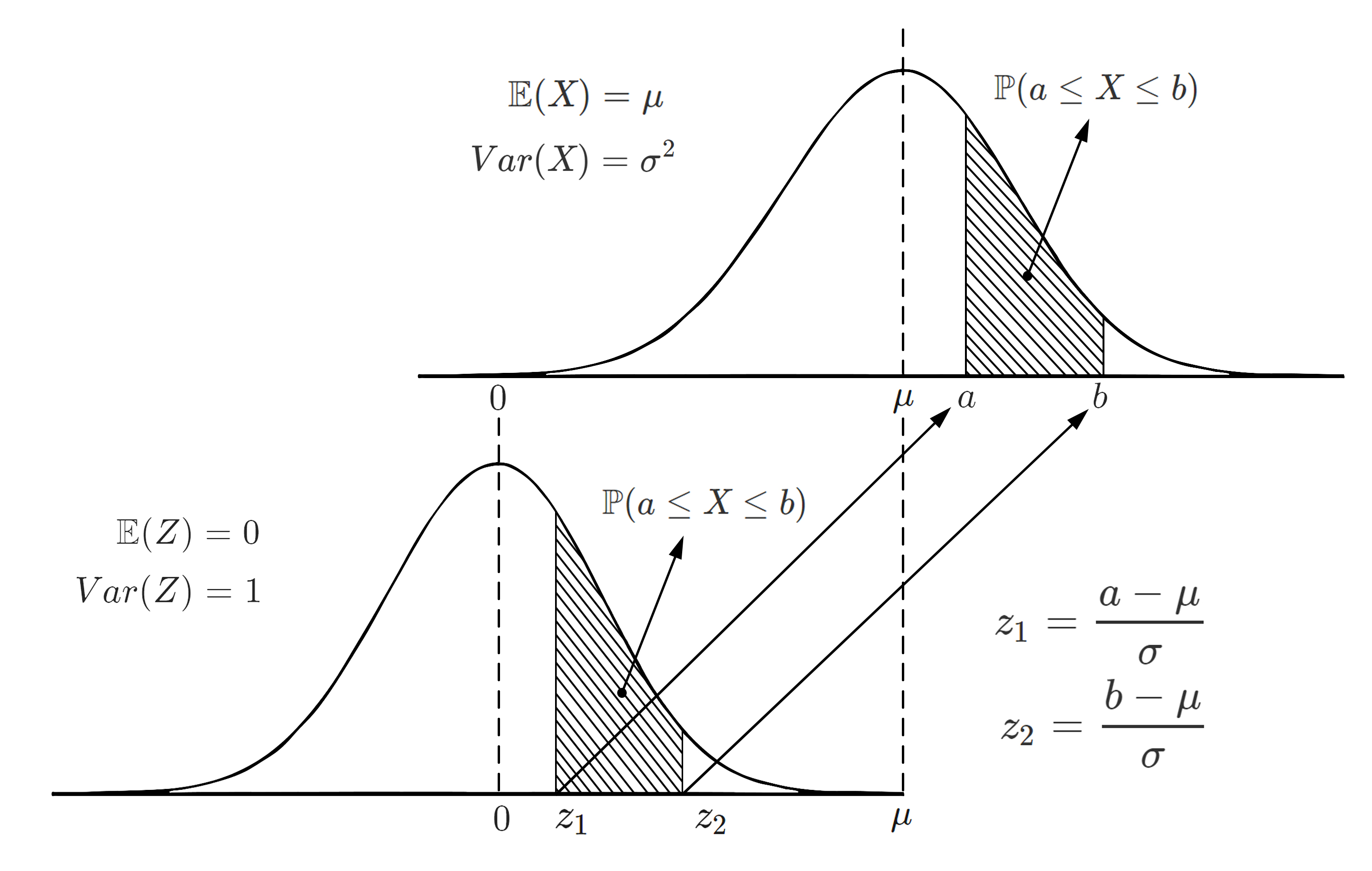
Si $X\sim N(\mu, \sigma^2)$, siendo $a$ y $b$ dos constantes
cualquiera, entonces si se realiza la transformación
$Z=\frac{x-\mu}{\sigma}$ conocida como estandarización, se tendrá
que $Z\sim N(0,1)$, con $z_1$ y $z_2$ las dos constantes
transformadas.
Propiedades
Si $X\sim N(\mu, \sigma^2)$, entonces al aplicar el teorema de
estandarización $Z=\frac{x-\mu}{\sigma} \sim N(0,1)$, y por tanto, si
$z_1$ y $z_2$ son constantes, se tendrá que
$\mathbb{P}(Z\leq z_1) = \mathbb{P}(Z\geq -z_1)$$\mathbb{P}(Z\geq z_1) = \mathbb{P}(Z\leq -z_1) = 1- \mathbb{P}(Z\leq z_1)$$\mathbb{P}(z_1\leq Z\leq z_2) = \mathbb{P}(Z\leq z_2) - \mathbb{P}(Z< z_1)$- Si
$z_1 = - z_2$entonces$\mathbb{P}(z_1\leq Z\leq z_2) = \mathbb{P}(-z_2\leq Z\leq z_2) =2\mathbb{P}(Z\leq z_2) - 1$ $Z_\alpha$es el valor de la variable aleatoria$Z\sim N(0,1)$tal que$\mathbb{P}(Z\geq Z_\alpha)=\alpha$, y$\mathbb{P}(Z\leq Z_\alpha)=1 - \alpha$
En donde, debe recordarse que, al ser la distribución normal una
distribución continua, la $\mathbb{P}(Z\leq z_1) = \mathbb{P}(Z< z_1)$
y $\mathbb{P}(Z\geq z_1) = \mathbb{P}(Z > z_1)$. Lo anterior debido a
que en la distribuciones continuas la probabilidad puntual es igual a
$0$.
Ejercicio
Suponga que poseemos una distribución normal estándar, tal que \(Z\sim N(0,1)\). Entonces, a partir de esta distribución y empleando la Tabla de la Distribución Normal Estándar, calcule
- \(\mathbb{P}(Z\leq 1.96)\)
- \(\mathbb{P}(Z> 2.13)\)
- \(\mathbb{P}(-2.42 <Z \leq 0.24)\)
- \(\mathbb{P}(Z>z) = 0.0129\)
Solución
Para calcular probabilidades con la tabla de la distribución normal estándar, es necesario tener en cuenta el funcionamiento de la tabla misma. Y para ello se presenta la siguiente imagen.
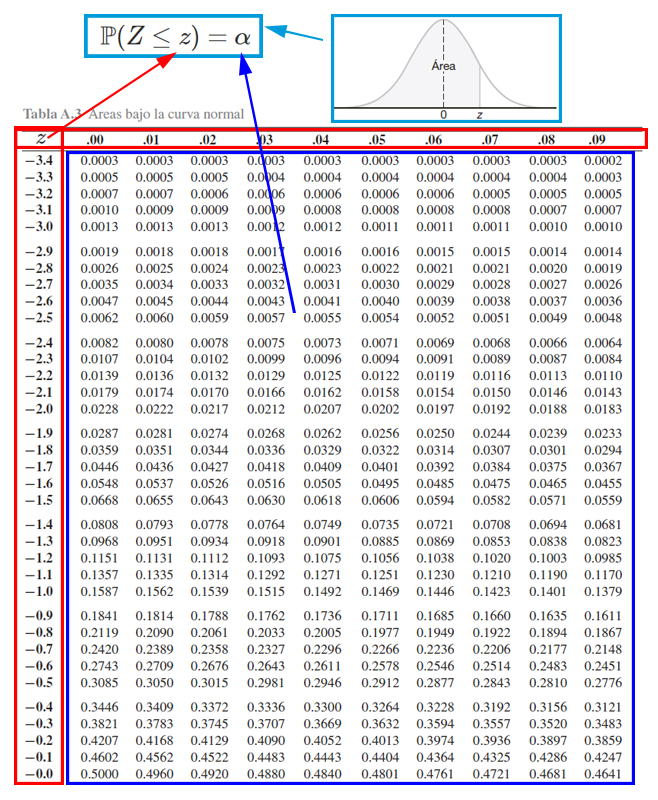
En donde, se aprecia que, los cuadros rojos representan los valores críticos \(z\) que se emplea para calcular probabilidades, en donde, el cuadro rojo de la parte izquierda muestra la parte entera y el primer decimal, mientras que el cuadro rojo de la parte superior muestra el segundo decimal. El cuadro azul representa las probabilidades \(\alpha\) que se desean calcular a partir de los valores críticos. Finalmente, el cuadro azul claro representa el funcionamiento de la tabla , la cual muestra las probabilidades que poseen la forma \(\mathbb{P}(Z<z)=\alpha\).
-
Con la explicación de la tabla en mente, la primera probabilidad a
calcular es \(\mathbb{P}(Z\leq 1.96)\). Entonces como esta probabilidad
tiene la estructura establecida por la tabla \(\mathbb{P}(Z\leq z)\),
será cuestión de buscar el valor crítico \(1.96\) para localizar la
probabilidad asociada, tal que se busca en la parte izquierda, el valor
\(1.9\) y en la parte superior el valor \(0.06\), y en donde se
encuentre el cruce de ambos valores, se encontrará el valor de la
probabilidad asociada a \(1.96\). Dicho procedimiento se muestra en la
siguiente imagen
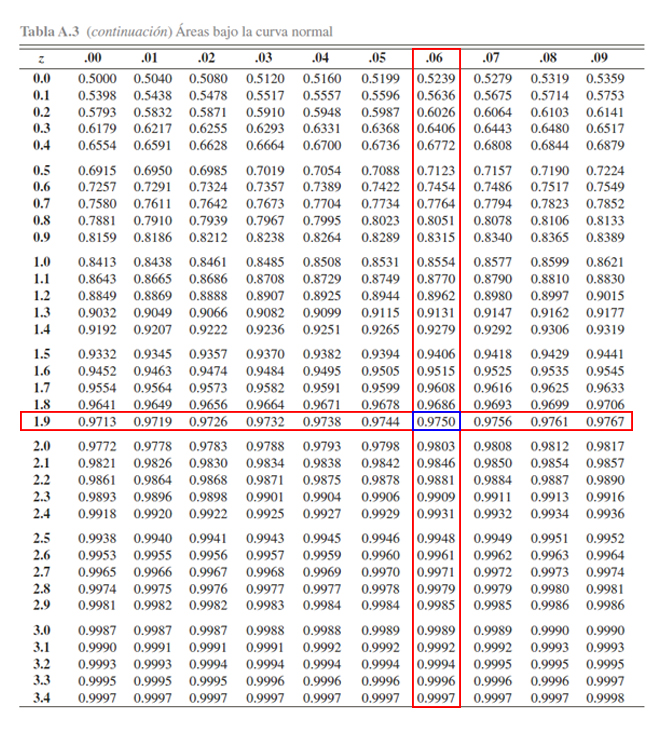Donde se aprecia que
\[\begin{align*}\mathbb{P}(Z\leq 1.96)=0.9750\end{align*}\]
-
A diferencia del punto anterior, observamos que la probabilidad
propuesta \(\mathbb{P}(Z> 2.13)\) tiene una estructura diferente a la
establecida por la tabla \(\mathbb{P}(Z\leq z)\), y por tanto, será
necesario emplear el complemento de la probabilidad propuesta para
obtener una estructura similar a la propuesta por la tabla, tal que
\[\begin{align*}
\mathbb{P}(Z> 2.13)= 1 - \mathbb{P}(Z\leq 2.13)
\end{align*}\] En donde, se aprecia que ahora podemos calcular la
\(\mathbb{P}(Z> 2.13)\), mediante el empleo de la
\(\mathbb{P}(Z\leq 2.13)\), la cual podemos buscar en la tabla
directamente. Para localizar \(\mathbb{P}(Z\leq 2.13)\), se busca el
valor \(2.1\) en la parte izquierda de la tabla, y el valor \(0.03\) en
la parte superior de la tabla, y en donde se encuentre el cruce de ambos
valores, se encontrará el valor de la probabilidad asociada a \(2.13\).
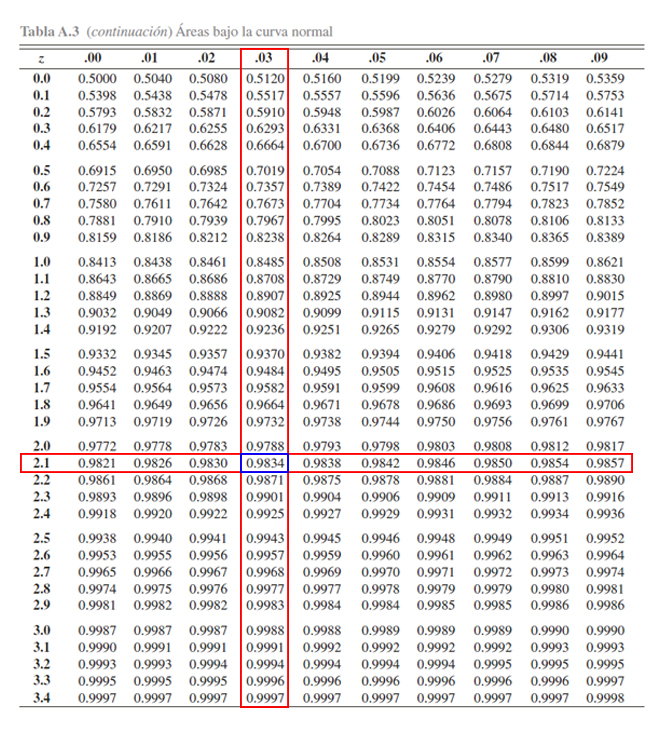Donde se aprecia que
\[\begin{align*}
\mathbb{P}(Z\leq 2.13)=0.9834
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(Z> 2.13)&= 1 - \mathbb{P}(Z\leq 2.13)\\
&= 1 - 0.9834 \\
&= 0.0166
\end{align*}\]
-
En este caso, se desea calcular la \(\mathbb{P}(-2.42 <Z \leq 0.24)\), y
se observa que la estructura de dicha probabilidad es diferente a la
establecida por la tabla \(\mathbb{P}(Z\leq z)\), pero también podemos
apreciar que si aplicamos las propiedades de la función de distribución
acumulada para el caso continuo, ya presentadas en la
Clase
08, podemos llevar la probabilidad de interés a la forma
\[\begin{align*}
\mathbb{P}(-2.42 <Z \leq 0.24) = \mathbb{P}(Z \leq 0.24) - \mathbb{P}(Z \leq -2.42)
\end{align*}\] obteniendo que la probabilidad
\(\mathbb{P}(-2.42 <Z \leq 0.24)\), puede calcularse mediante el empleo
de las probabilidades acumuladas \(\mathbb{P}(Z \leq 0.24)\) y
\(\mathbb{P}(Z \leq -2.42)\), las cuales pueden calcularse en la tabla
de forma similar a los dos puntos anteriores.
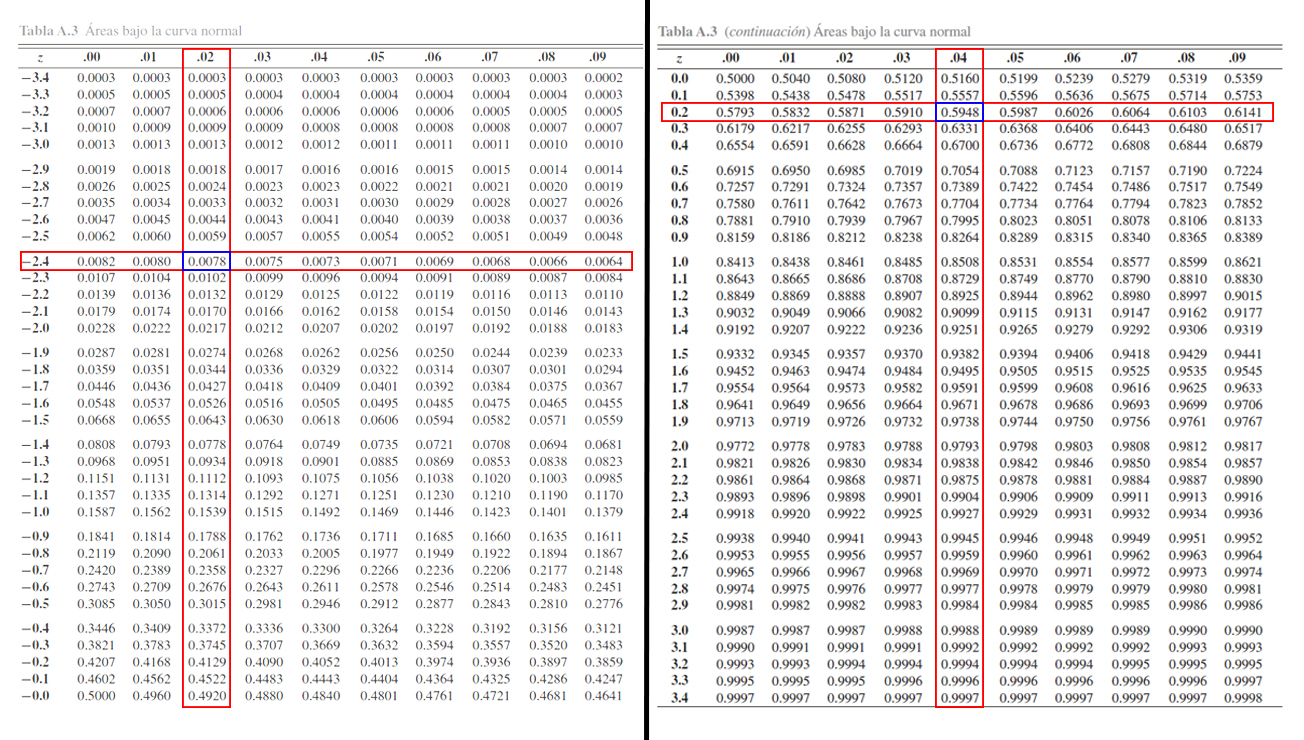Donde se aprecia que
\[\begin{align*}
\mathbb{P}(Z \leq -2.42)=0.0078 \quad \text{ y } \quad \mathbb{P}(Z \leq 0.24)=0.5948
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(-2.42 <Z \leq 0.24) &= \mathbb{P}(Z \leq 0.24) - \mathbb{P}(Z \leq -2.42)\\
&= 0.5948 - 0.0078 \\
&= 0.587
\end{align*}\]
-
En este punto, a diferencia de los puntos anteriores, no están dando el
valor de la probabilidad y nos piden encontrar el valor crítico \(z\).
Es decir debemos calcular el valor crítico asociado a la probabilidad
\[\begin{align*}
\mathbb{P}(Z>z) = 0.0129
\end{align*}\]
Y para ello, debemos llevar inicialmente la estructura de la
probabilidad, a la estructura manejada por la tabla, tal que
\[\begin{align*}
\mathbb{P}(Z>z) &= 0.0129 \\
1 - \mathbb{P}(Z\leq z) &= 0.0129 \\
1- 0.0129 &= \mathbb{P}(Z\leq z) \\
0.9871 &= \mathbb{P}(Z\leq z)
\end{align*}\]
En donde observamos que la probabilidad \(\mathbb{P}(Z\leq z)\) ya posee
la estructura de la tabla, y en consecuencia, podemos proceder a
encontrar el valor crítico \(z\), buscando el valor de la probabilidad
\(0.9871\) en la parte interior de la tabla, y luego buscando cual es el
valor crítico \(z\) asociado a dicha probabilidad.
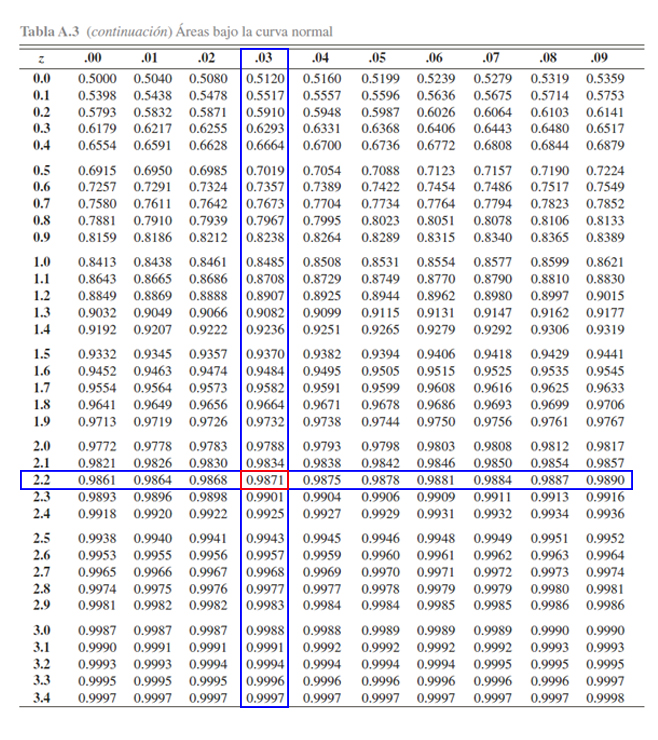En la tabla se aprecia, que al buscar la probabilidad \(0.9871\)
encontramos que el valor crítico \(z\) asociado es de \(2.24\), es decir
\[\begin{align*}
\mathbb{P}(Z\leq 2.24) &= 0.9871
\end{align*}\]
o equivalentemente
\[\begin{align*}
\mathbb{P}(Z > 2.24) &= 0.0129
\end{align*}\]
Ejercicio
Suponga que cierto tipo de batería para celular dura en promedio \(5\) años con una desviación estándar de \(1.2\) años. Si se sabe por experiencia que la distribución de las baterías se distribuye normalmente, cuál es la probabilidad de que una batería de celular dure al menos \(4\) años?
Solución
En este caso estamos interesados en que la batería de una celular dure
al menos \(4\) años, es decir, queremos calcular la siguiente
probabilidad. \[\begin{align*}
\mathbb{P}(X \geq 4)
\end{align*}\] Pero en este caso tenemos que la distribución de los
datos no se distribuye \(N(0,1)\), si no que se distribuye
\(N(5, 1.2)\), y por ello debemos aplicar el teorema de estandarización,
con el fin de llevar la distribución \(N(5, 1.2)\) a una normal
estándar, tal que \[\begin{align*}
\mathbb{P}(X \geq 4)&=\mathbb{P}\left(\frac{X-\mu}{\sigma}\geq \frac{4-5}{1.2}\right)\\
\mathbb{P}(X \geq 4)&=\mathbb{P}\left(\frac{X-\mu}{\sigma}\geq \frac{4-5}{1.2}\right)\\
\mathbb{P}(X \geq 4)&=\mathbb{P}(Z \geq -0.83)
\end{align*}\] En donde \(Z\sim N(0,1)\). Ahora, como la estructura de
la probabilidad de \(Z\) no posee la estructura de la probabilidad de se
maneja en la tabla, entonces procedemos a calcular el complemento de la
probabilidad, tal que \[\begin{align*}
\mathbb{P}(Z \geq -0.83)&= 1 - \mathbb{P}(Z < -0.83) \\
\end{align*}\] y en consecuencia podemos ahora buscar la probabilidad
\(\mathbb{P}(Z < -0.83)\) en la tabla de la distribución normal
estándar, de la siguiente manera
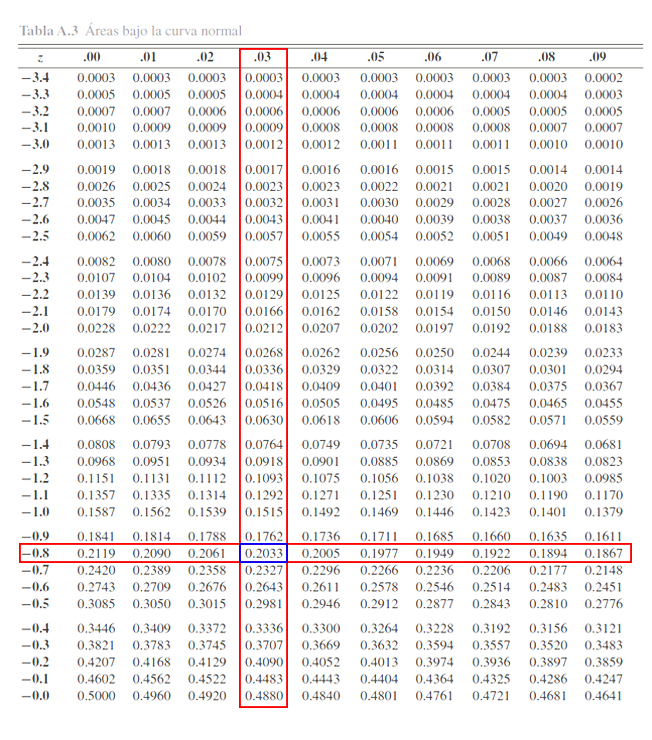Donde se aprecia que
\[\begin{align*}
\mathbb{P}(Z < -0.83)=0.2033
\end{align*}\]
y por tanto, se tendrá que
\[\begin{align*}
\mathbb{P}(Z \geq -0.83)&= 1 - \mathbb{P}(Z < -0.83) \\
&= 1 - 0.2033 \\
&= 0.7967
\end{align*}\]
lo cual es equivalente a
\[\begin{align*}
\mathbb{P}(X \geq 4)&= \mathbb{P}(Z \geq -0.83) \\
&= 0.7967
\end{align*}\]
En consecuencia, se tendrá que la probabilidad de que una batería de
celular dure al menos \(4\) años, es del \(76.67\%\).
Teoremas de Aproximación
Teorema de Aproximación Binomial a Normal
Si $X\sim b(n,p)$ con $n$ grande $(n\geq 30)$ y $p$ cercano a
0.5 $(p\approx 0.5)$ entonces se dice que
$X\stackrel{a}{\sim}N(\mu,\sigma^2)$ donde $\mu = np$ y
$\sigma^2 = np(1-p)$.
Además, se tendrá que $Z\stackrel{a}{\sim}N(0,1)$, tal que
\begin{align*} Z=\frac{x-np}{\sqrt{np(1-p)}}\stackrel{a}{\sim}N(0,1) \end{align*}
La aproximación será buena si $np$ y $n(1-p)>5$.
Nota: Para realizar la aproximación de binomial a normal, se debe
usar un factor de corrección de continuidad de 0.5, así
\begin{align*} \text{Binomial} & & & & \text{Normal} \quad \quad \quad \quad \quad \\ \mathbb{P}(X\leq a) & & & & \mathbb{P}(X\leq a + 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X<a) & & & & \mathbb{P}(X\leq a - 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X\geq a) & & & & \mathbb{P}(X\geq a - 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X>a) & & & & \mathbb{P}(X\geq a + 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X=a) & & & & \mathbb{P}(a - 0.5 \leq X\leq a + 0.5) \end{align*}
Ejercicio
Suponga que el ministerio de salud realiza un estudio sobre la probabilidad de que una persona de \(40\) años muera antes de la edad de jubilación a los \(62\) años, y encuentra que dicha probabilidad es de \(15\%\). Si se toma como referencia un grupo de \(1500\) personas que posee \(40\) años de edad, cuál es la probabilidad de que menos de \(220\) muera antes de la edad de jubilación?.
Solución
En este caso estamos interesados en calcular cuál es la probabilidad de
que menos de \(220\) personas mueran antes de los \(62\) años, y se toma
como grupo de estudio un total de \(1500\) personas, sabiendo que la
probabilidad de que mueran antes de los \(62\) es del \(15\%\), es
decir, tenemos que \(X\sim b(n=1500, p=0.15)\), y deseamos calcular
\[\begin{align*}
\mathbb{P}(X<220)&= \sum_{x=0}^{219} \left(\begin{array}{c}1500\\ x\end{array}\right) (0.15)^x(0.85)^{1500-x} \\
&= 0.3480602
\end{align*}\] Es de anotar que el valor de la probabilidad presentada
no es posible calcularla en una calculadora, debido a que las
limitaciones que posee ésta, no permiten calcular una combinatoria de
tal magnitud, y en consecuencia, resulta el intento de calcular dicha
sumatoria en el mensaje \(Math\) \(ERROR\). Y es por ello que la
probabilidad anterior se calculó en el programa R para poder
tomar dicho valor como referencia para compararlo con el valor de la
aproximación normal.
Ahora, dado que no es posible calcular dicha probabilidad en la
calculadora, se procede a la aplicación del teorema de aproximación a la
distribución normal, si \(X\sim b(n=1500, p=0.15)\) entonces se tendrá
que la media será igual a
\(X\stackrel{a}{\sim}N(\mu=np,\sigma^2=np(1-p))\), en donde
\[\begin{align*}
\mu &= np \\
&= 1500(0.15) \\
&= 225
\end{align*}\]
y la varianza igual a
\[\begin{align*}
\sigma^2 &= np(1-p) \\
&= 1500(0.15)(0.85) \\
&= 191.25
\end{align*}\]
Ahora, conocidos los parámetros \(\mu=225\) y
\(\sigma=\sqrt{191.25}=13.82932\), se procede al cálculo de la
probabilidad de interés, en donde, al aplicar el factor corrector de
continuidad a la probabilidad se tendrá que \[\begin{align*}
\text{Binomial} & & & & \text{Normal} \quad \quad \quad \quad \quad \\
\mathbb{P}(X< 220) & & & & \mathbb{P}(X\leq 220 - 0.5) \quad \quad \quad \quad \; \\
\end{align*}\] es decir que, si \(X\sim b(n=1500, p=0.15)\) estamos
interesados en calcular \(\mathbb{P}(X< 220)\), mientras que si
\(X\stackrel{a}{\sim}N(\mu=225,\sigma^2=191.25)\) estaríamos interesados
en calcular \(\mathbb{P}(X\leq 219.5)\). Por tanto, al aplicar el
teorema de estandarización para transformar dicha probabilidad una
distribución normal estándar, se tendrá que
\[\begin{align*}
\mathbb{P}(X \leq 219.5) &= \mathbb{P}\left(\frac{X-\mu}{\sigma}\leq \frac{219.5 - 225}{13.82932}\right)\\
&= \mathbb{P}(Z \leq -0.40)
\end{align*}\]
En donde se aprecia que la \(\mathbb{P}(Z \leq -0.40)\) tiene la misma
estructura establecida por la tabla de distribución normal estándar
\(\mathbb{P}(Z\leq z)\), y por tanto será cuestión de buscar el valor
crítico \(0.40\) en la tabla, para encontrar la probabilidad asociada a
dicho valor, tal que
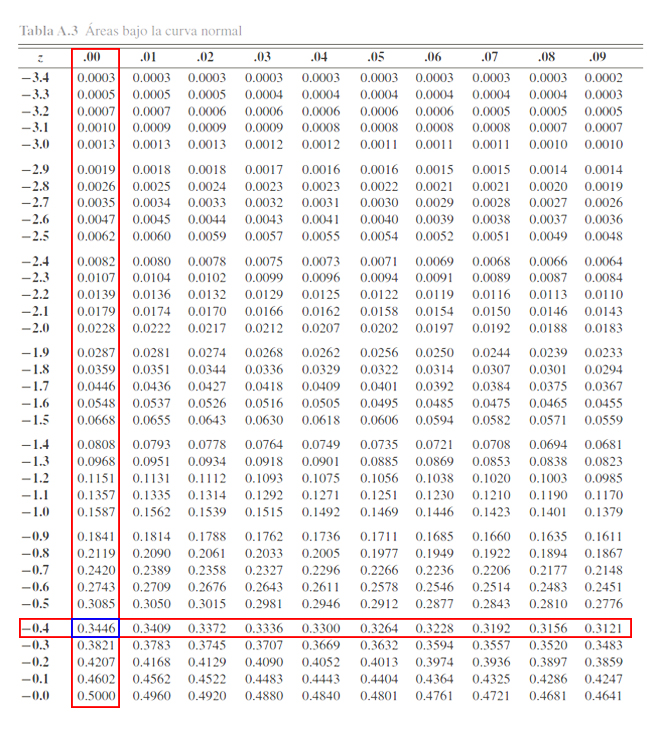Donde se aprecia que
\[\begin{align*}
\mathbb{P}(Z \leq -0.40)=0.3446
\end{align*}\] o equivalentemente, se tendrá que
\[\begin{align*}
\mathbb{P}(X \leq 219.5) &= \mathbb{P}(Z \leq -0.40) \\
&= 0.3446
\end{align*}\] Es decir que la probabilidad aproximada de que menos de
\(220\) personas mueran de los \(1500\) antes de llegar a los \(62\)
años, es del \(34.46\%\).
Al comparar el resultado exacto de la distribución binomial \(34.81\%\),
con respecto al resultado aproximado con la distribución normal
\(34.46\%\), se aprecia que la diferencia es muy pequeña, y en
consecuencia, se dice que la distribución normal ofrece una buena
aproximación para la distribución binomial.
Teorema de Aproximación Poisson a Normal
Si $X\sim P(\lambda)$ con $\lambda$ grande $(\lambda\geq 30)$
entonces se dice que $X\stackrel{a}{\sim}N(\mu,\sigma^2)$ donde
$\mu = \lambda$ y $\sigma^2 = \lambda$.
Además, se tendrá que $Z\stackrel{a}{\sim}N(0,1)$, tal que
\begin{align*} Z=\frac{x-\lambda}{\sqrt{\lambda}}\stackrel{a}{\sim}N(0,1) \end{align*}
Nota: Para realizar la aproximación de Poisson a Normal, se debe
usar el mismo factor de corrección de continuaidad de 0.5, así
\begin{align*} \text{Poisson} & & & & \text{Normal} \quad \quad \quad \quad \quad \\ \mathbb{P}(X\leq a) & & & & \mathbb{P}(X\leq a + 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X<a) & & & & \mathbb{P}(X\leq a - 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X\geq a) & & & & \mathbb{P}(X\geq a - 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X>a) & & & & \mathbb{P}(X\geq a + 0.5) \quad \quad \quad \quad \; \\ \mathbb{P}(X=a) & & & & \mathbb{P}(a - 0.5 \leq X\leq a + 0.5) \end{align*}