Jorge Iván Pérez

Variables aleatorias

Es una función que asocia un número real a cada elemento del espacio muestral $S$ . Comúnmente las variables aleatorias se denotan por letras mayúsculas del final del abecedario $(X,Y,Z)$ y a los valores observados por letras minúsculas $(x,y,z)$ .

Las variables aleatorias se pueden clasificar en tres tipos

Variables Bernoulli: Cualquier variable aleatoria cuyos posibles valores sean 0 o 1. Por ejemplo: Productos exentos de IVA; Cumplimientos de pronóstico
Variables discretas: Son aquellas que tienen un número finito de posibilidades o una serie interminable de elementos como números enteros existentes (es decir, es enumerable). Por ejemplo: El número de personas que habitan en una manzana; El número reformas que hay que hacerle a un edificio
Variables continuas: Son aquellas que contienen un número infinito de posibilidades, o igual número de puntos que un segmento de recta. Por ejemplo: Los costos variables que pueden incurrir una empresa en un mes; Los beneficios recibidos por la construcción de una vía

Distribución de probabilidad discreta

Se dice que el conjunto de pares ordenados $(x,p(x))$ es una función de masa de probabilidad $(fmp)$ de la variable aleatoria discreta $X$ , si para cualquier valor posible de $X$ se cumple que

$p(x)\geq0$ para todo $x \in$ en el dominio de $X$
$\sum_x p(x)=1$
$\mathbb{P}(X\in A)= \sum_{x\in A}p(x) $ con $A$ un conjunto de valores $\in$ al dominio de $X$ .

Ejercicio

Suponga que se realiza un estudio para la adecuación de la zona de urgencias de un hospital y para ello necesitan conocer el número de ambulancias que llegan a un hospital en una hora, encontrando que la función de distribución de probabilidad está dada por

$X$	$0$	$1$	$2$	$3$	$4$	$5\text{ o más}$
$p(x)$	$0.0498$	$0.1494$	$0.2240$	$0.2240$	$0.1680$	$0.1848$

Si la probabilidad de que lleguen al menos $4$ ambulancias en una hora es muy alta, el hospital considerará ampliar el estacionamiento, de otro modo, lo dejará tal y como está. Basado en ésto, aconsejaría usted al hospital que es necesario ampliar el estacionamiento?

Solución

Como $X$ es la variable aleatoria del número de ambulancias que llegan al hospital en una hora, se tendrá que nos preguntan por la probabilidad \[\begin{align*} \mathbb{P}(X>=4) \end{align*}\] la cual, al ser una variable aleatoria discreta podremos calcularla mediante sumatorias, tal que \[\begin{align*} \mathbb{P}(X\geq 4) &= 1 - \mathbb{P}(X < 4) \\ &= 1 - \sum_{x=0}^{3} p(x) \\ &= 1 - [p(0) + p(1) + p(2) + p(3)] \\ &= 1 - [p(0) + p(1) + p(2) + p(3)] \\ &= 1 - [0.0498 + 0.1494 + 0.2240 + 0.2240] \\ &= 1 - 0.6472 \\ &= 0.3528 \\ \end{align*}\] Es decir, que se tendrá una probabilidad del $35.28\%$ de que lleguen al menos $4$ ambulancia en una hora

Función de distribución acumulada caso discreto

La función de distribución acumulada $(fda)$ denotada por $F(x)$ , para una variable aleatoria discreta $X$ con distribución de probabilidad $p(x)$ es de la forma \begin{align*} F(x)=P(X\leq x)=\sum_{t\leq x}p(t) \quad \quad -\infty<x<\infty \end{align*}

Para cualquier $x$ dentro del dominio de $X$ , $F(x)$ será la suma acumulada de todos los $X$ menores a $x$ , evaluados en $f(x)$ .

Nota: Si se quieren calcular probabilidades con la función de distribución acumulada en el caso discreto, entonces, si $a$ y $b$ son dos números constantes enteros, deberán tenerse en cuenta las siguientes reglas

$\mathbb{P}(a \leq X \leq b) = \mathbb{P}(X \leq b) - \mathbb{P}(X < a)$
$\mathbb{P}(a < X \leq b) = \mathbb{P}(X \leq b) - \mathbb{P}(X \leq a)$
$\mathbb{P}(a \leq X < b) = \mathbb{P}(X < b) - \mathbb{P}(X < a)$
$\mathbb{P}(a < X < b) = \mathbb{P}(X < b) - \mathbb{P}(X \leq a)$
$\mathbb{P}(X \geq a) = 1 - \mathbb{P}(X < a)$
$\mathbb{P}(X > a) = 1 - \mathbb{P}(X \leq a)$
$\mathbb{P}(X \leq b) = F(b)$
$\mathbb{P}(X < b) = F(b - 1)$

Ejercicio

$X$	$0$	$1$	$2$	$3$	$4$	$5\text{ o más}$
$p(x)$	$0.0498$	$0.1494$	$0.2240$	$0.2240$	$0.1680$	$0.1848$

Construya la función de distribución acumulada asociada al número de ambulancias que llegan a la zona de urgencias en una hora y calcule la probabilidad de que este vañpr sea al menos de $4$.

Solución

Como la función de distribución acumulada parte de la función de masa de probabilidad, partimos de esta tabla y se procede a realizar el cálculo de la función de distribución acumulada $F(x)$. Para ello, debemos calcular las siguientes probabilidades $F(0) = \mathbb{P}(X\leq 0)$, $F(1) = \mathbb{P}(X\leq1)$, $F(2) = \mathbb{P}(X\leq2)$, $F(3) = \mathbb{P}(X\leq3)$ y $F(4) = \mathbb{P}(X\leq4)$. \[\begin{align*} F(0) & = \mathbb{P}(X\leq0) = p(0) = 0.0498 \\ F(1) & = \mathbb{P}(X\leq1) = p(0) + p(1) = 0.0498 + 0.1494 = 0.1992\\ F(2) & = \mathbb{P}(X\leq2) = \sum_{x=0}^{2} p(x) = 0.0498 + 0.1494 + 0.2240 = 0.4232 \\ F(3) & = \mathbb{P}(X\leq3) = \sum_{x=0}^{3} p(x) = 0.0498 + 0.1494 + 0.2240 + 0.2240 = 0.6472 \\ F(4) & = \mathbb{P}(X\leq4) = \sum_{x=0}^{4} p(x) = 0.0498 + 0.1494 + 0.2240 + 0.2240 + 0.2240 = 0.8712 \end{align*}\] Entonces, mediante el empleo de estas probabilidades, podemos construir la función de distribución acumulada para la variable aleatoria $X$, tal que \[\begin{align*} F(x) = \begin{cases} 0 & x<0 \\ 0.0498 & 0\leq x<1 \\ 0.1992 & 1\leq x<2 \\ 0.4232 & 2\leq x<3 \\ 0.6472 & 3\leq x<4 \\ 0.8712 & 4\leq x<5 \\ 1 & x\geq5 \end{cases} \end{align*}\] En donde se aprecia, que para valores menores a $0$, no hay ninguna probabilidad definida, para valores mayores o iguales a $0$ pero menores que $1$ solo está definido $F(0)=p(0)$, para valores mayores o iguales a $1$ pero menores que $2$ está definido $F(1)=p(0)+p(1)$, para valores mayores o iguales a $2$ pero menores que $3$ está definido $F(2)=p(0)+p(1)+p(2)$, y así sucesivamente.

Ahora dado que estamos interesados en calcular la probabilidad de que el número de ambulancias que llegan a la zona de urgencias en una hora sea de al menos $4$ ambulancias, se tendrá que se debe calcular \[\begin{align*} \mathbb{P}(X \geq 4) \end{align*}\] Entonces, siguiendo las reglas anteriormente expuestas, dicha probabilidad puede calcularse mediante distribuciones acumuladas como \[\begin{align*} \mathbb{P}(X \geq 4) & = 1 - F(4-1) \\ & = 1 - F(3) \\ & = 1 - 0.6472 \\ & = 0.3528 \end{align*}\] y por tanto, se tendrá que la probabilidad de que en una hora lleguen al menos $4$ ambulancias a un hospital es del $35.28\%$.

Algunas distribuciones de probabilidad discreta

Proceso Bernoulli

Un proceso Bernoulli es aquel que cumple

El experimento consta de ensayos repetidos bajo las mismas condiciones.
Cada ensayo produce un resultado que se puede clasificar como éxito o fracaso.
La probabilidad de éxito se denota por $p$ y permanece constante de un ensayo a otro.
Los ensayos repetidos son independientes entre si.

Ejemplo

Los siguientes, son algunos ejemplos de casos que pueden considerarse como Procesos Bernoulli, debido a que cumplen las $4$ condiciones propuestas anteriormente.

El número de inversionistas que están a favor de un proyecto.
Verificar los metas que son alcanzadas en un proyecto.
El número de trabajadores de sexo femenino que trabajan en un proyecto.

Ensayo de Bernoulli

Si la probabilidad de éxito de un experimento es $p$ , entonces la probabilidad de fallo debe ser $1-p$ y la función de probabilidad de la variable aleatoria $X\sim Be(p)$ para un ensayo Bernoulli será \begin{align*} f(x) = p^x(1-p)^{1-x} \quad \quad x=0,1 \end{align*}

En Excel, pueden calcularse probabilidades Bernoulli mediante la función DISTR.BINOM.N(), con $\text{ensayos}=1$ .

Media y Varianza Ensayo de Bernoulli

Si $X\sim Be(p)$ , entonces se puede probar que la media y la varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X)=p \quad \quad Var(X)=p(1-p) \end{align*}

Ejercicio

Por experiencia se sabe que, de $3$ de cada $5$ meses, una empresa obtiene utilidades superiores a las esperadas. Si se selecciona un mes aleatoriamente,

Cuál es la probabilidad de que en éste no se haya superado las utilidades esperadas por la empresa?
Calcule la media y desviación estándar de que en dicho mes no se superen las utilidades esperadas?

Solución

En este caso estamos interesados en la variable $X$, que representa el número de veces que no se superan las utilidades esperadas, en donde sabemos que si, $3$ de cada $5$ meses se obtienen utilidades superiores a las esperadas, se tendrá que $2$ de cada $5$ no se superarán dichas utilidades. Por tanto al aplicar la definición de frecuencia relativa se tiene que \[\begin{align*} p &= \frac{\text{Número de éxitos}}{\text{Número de muestras}}\\ &= \frac{2}{5} \\ &= 0.4 \end{align*}\] siendo $p$ la probabilidad de que no se superen las utilidades en un mes. Ahora, la probabilidad de que en un mes no se haya superado las utilidades esperadas por la empresa será igual a \[\begin{align*} \mathbb{P}(X = 1) &= p(1-p)^{1-x} \\ &= 0.4(0.6)^{1-1} \\ &= 0.4(0.6)^0 \\ &= 0.4 \end{align*}\] es decir, que se tendrá una probabilidad del $60\%$ de que no se superen las utilidades esperadas en un mes seleccionado aleatoriamente.
Ahora, como estamos interesados en el valor promedio de un proceso Bernoulli el cual es igual a $p$, se tendrá que \[\begin{align*} \mathbb{E}(X) &= p \\ &= 0.4 \end{align*}\] Por su parte, para calcular la desviación estándar se requiere calcular inicialmente la varianza de la variable aleatoria, la cual está dada por \[\begin{align*} Var(X) &= p(1-p) \\ &= 0.4(0.6) \\ &= 0.24 \end{align*}\] y a partir de éste valor, se tendrá que la desviación estándar es igual a \[\begin{align*} Sd(X) &= \sqrt{Var(X)} \\ &= \sqrt{0.24} \\ &= 0.4898979 \end{align*}\] Por tanto, al seleccionar un mes aleatoriamente, se espera que en promedio $0.4$ de las veces no se superen las utilidades esperadas en un mes seleccionado aleatoriamente, con una desviación estándar de $0.4889$.

Distribución Binomial

Si $X$ es la variable aleatoria del número de éxitos de $n$ ensayos de Bernoulli, con probabilidad de éxito $p$ , entonces se dice que $X\sim b(n,p)$ tal que \begin{align*} f(x) = \left(\begin{array}{c}n\\ x\end{array}\right)p^x(1-p)^{n-x} \quad \quad x=0,1,\ldots,n \end{align*}

Nota: Esta distribución es usada cuando se realiza muestreo con reemplazo o en poblaciones infinitas en donde es posible suponer que la probabilidad de éxito $p$ es la misma en cada ensayo Bernoulli.

En Excel, pueden calcularse probabilidades Binomiales mediante la función DISTR.BINOM.N().

Media y Varianza Distribución Binomial

Si $X\sim b(n,p)$ , entonces se puede probar que la media y varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X)=np \quad \quad Var(X)=np(1-p) \end{align*}

Ejercicio

Por experiencia se sabe que, de $3$ de cada $5$ meses, una empresa obtiene utilidades superiores a las esperadas. Si se selecciona $10$ meses aleatoriamente,

Cuál es la probabilidad de que en no más de $3$ meses no se obtengan utilidades superiores a las esperadas?
Cuál es la probabilidad de que en no menos de $6$ pero menos de $8$ meses no se obtengan utilidades superiores a las esperadas?
Cuál es el número promedio y desviación estándar del número de meses en los cuales no se obtienen utilidades superiores a las esperadas?.

Solución

En este caso estamos interesados en la variable $X$, que representa el número de veces que no se superan las utilidades esperadas en $n=10$ meses, en donde sabemos que si, $3$ de cada $5$ meses se obtienen utilidades superiores a las esperadas, se tendrá que $2$ de cada $5$ no se superarán dichas utilidades. Por tanto al aplicar la definición de frecuencia relativa se tiene que \[\begin{align*} p &= \frac{\text{Número de éxitos}}{\text{Número de muestras}}\\ &= \frac{2}{5} \\ &= 0.4 \end{align*}\] siendo $p$ la probabilidad de que no se superen las utilidades en un mes.

Basados en lo anterior, en este caso estamos interesados en calcular la probabilidad de que no más de $3$ meses no se obtengan utilidades superiores a las esperadas?, lo cual puede representarse mediante la siguiente probabilidad \[\begin{align*} P(X\leq 3) &= \sum_{x=0}^3 \left(\begin{array}{c}10\\ x\end{array}\right)0.4^x(1-0.4)^{10-x} \\ &= \left(\begin{array}{c}10\\ 0\end{array}\right)0.4^0(0.6)^{10-0} + \ldots + \left(\begin{array}{c}10\\ 3\end{array}\right)0.4^3(0.6)^{10-3} \\ &= 0.0060466 + 0.0403108 + 0.1209324 + 0.2149908 \\ &= 0.3822806 \end{align*}\] Es decir, la probabilidad de que como máximo en $3$ meses de los $10$ seleccionados aleatoriamente, no se superen las utilidades esperadas en un mes, es del $38.23\%$.
Ahora, se tiene interés en conocer la probabilidad de que en no menos de $6$ pero en menos de $8$ meses no se obtengan utilidades superiores a las esperadas, la cual está dada por \[\begin{align*} P(6 \leq x < 8) &= \sum_{x=6}^{7} \left(\begin{array}{c}10\\ x\end{array}\right)0.4^x(1-0.4)^{10-x} \\ &= \left(\begin{array}{c}10\\ 6\end{array}\right)0.4^6(0.6)^{10-6} + \ldots + \left(\begin{array}{c}10\\ 7\end{array}\right)0.4^{7}(0.6)^{10-7} \\ &= 0.1539441 \end{align*}\] Es decir que, la probabilidad de que en como mínimo $6$ pero menos de $8$ meses de los $10$ seleccionados aleatoriamente, no se superen las utilidades esperadas en un mes, es del $15.39\%$.
Finalmente, se tiene interés en conocer cual será el número promedio y desviación estándar, de meses en los cuales no se superará las utilidades esperados, cuando se realiza la selección aleatoria de $10$. Al aplicar la formula del promedio de la distribución binomial, se tiene que \[\begin{align*} \mathbb{E}(X) & = np \\ & = 10(0.4)\\ \mathbb{E}(X) & = 4 \end{align*}\] mientras que, al aplicar la formula de la varianza de la distribución binomial se tendrá que \[\begin{align*} Var(X) &= np(1-p) \\ &= 10(0.4)(1-0.4)\\ Var(X) & = 2.4 \end{align*}\] y con este valor, se realiza el cálculo de la desviación estándar \[\begin{align*} Sd(X) &= \sqrt{Var(X)} \\ &= \sqrt{Var(2.4)} \\ Sd(X) & = 1.549193 \end{align*}\] De lo anterior se tiene que, al realizar la selección aleatoria de $10$ meses, se espera que en promedio en $4$ meses no se superen las utilidades esperadas, con una desviación estándar de $1.549193$ meses.

Distribución Hipergeométrica

Si $X$ es el número de éxitos de una muestra completamente aleatoria de tamaño $n$ extraída de una población $N$ compuesta por $M$ éxitos y $(N-M)$ fracasos, entonces la distribución de $X\sim h(N,M,n)$ , con función de masa de probabilidad \begin{align*} p(x)=\frac{\left(\begin{array}{c}M\\ x\end{array}\right) \left(\begin{array}{c}N-M\\ n-x\end{array}\right)}{\left(\begin{array}{c}N\\ n\end{array}\right)} \end{align*}

con $x$ un entero que satisface la condición $\max\{0, M-(N-n)\} \leq x \leq \min\{M,n\}$ .

Nota: Esta distribución es usada cuando se realiza muestreo sin reemplazo, en poblaciones finitas donde hay $M$ éxitos de un total de $N$ objetos, de los cuales se seleccionan $n$ objetos a la vez.

En Excel, pueden calcularse probabilidades Hipergeométricas mediante la función DISTR.HIPERGEOM.N().

Media y Varianza Hipergeométrica

Si $X\sim h(N,M,n)$ , entonces se puede probar que la media y varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X)=n\frac{M}{N} \quad \quad Var(X)=\left(\frac{N-n}{N-1}\right)\left(\frac{M}{N}\right)\left(1-\frac{M}{N}\right) \end{align*}

Ejercicio

Suponga una junta directiva compuesta por $15$ personas, las cuales son las responsables de decidir si se lleva o no a cabo un proyecto de inversión. Se hace un sondeo para saber cuales inversionistas están a favor del proyecto de inversión y se encuentra que $10$ de éstas están a favor de realizar el proyecto.

Si el día de votación solo asisten $9$ personas a la junta,

Cuál es la probabilidad de que la mayoría apruebe llevar a cabo el proyecto de inversión?.
Cuál es la media y desviación estándar del número de personas que apoyarán realizar la inversión?

Solución

En el primer punto estamos interesados en conocer la probabilidad de que entre las $9$ personas que asistieron a la junta, la mayoría apruebe llevar a cabo el proyecto de inversión, y para ello se requeriría que al menos $5$ vote a favor, es decir \[\begin{align*} \mathbb{P}(X\geq5) \end{align*}\] Donde $X$: representa el número de personas que están a favor de realizar el proyecto de inversión, de las $9$ que asistieron a la junta. Además, de la información suministrada tenemos que el total de miembros de la junta es de de $N=15$ personas de las cuales se había encontrado que $M=10$ estaba a favor de realizar el proyecto. Entonces, como $n=9$ asistieron la junta de votación, se tendrá la siguiente distribución de probabilidad \[\begin{align*} p(x)=\frac{\left(\begin{array}{c}10\\ x\end{array}\right) \left(\begin{array}{c}5\\ 9-x\end{array}\right)}{\left(\begin{array}{c}15\\ 9\end{array}\right)} \end{align*}\] la cual está definida para \[\begin{align*} \max\{0, M-(N-n)\} &\leq x \leq \min\{M,n\} \\ \max\{0, 10-(15-9)\} &\leq x \leq \min\{10,9\} \\ \max\{0, 10-(6)\} &\leq x \leq \min\{10,9\} \\ \max\{0, 4\} &\leq x \leq \min\{10,9\} \\ 4 &\leq x \leq 9 \\ \end{align*}\] en donde, al ser la distribución hipergeométrica una distribución discreta, tendremos que el número de miembros a favor del proyecto puede ser de $x=4, 5, \ldots 9$.

Ahora, al emplear esta función de distribución para calcular la probabilidad de interés tendremos que \[\begin{align*} \mathbb{P}(X\geq5) &= \sum_{x=5}^9 \frac{\left(\begin{array}{c}10\\ x\end{array}\right) \left(\begin{array}{c}5\\ 9-x\end{array}\right)}{\left(\begin{array}{c}15\\ 9\end{array}\right)} \\ &= 0.2517 + 0.4196 + 0.2398 + 0.045 + 0.002\\ &=0.958042 \end{align*}\] En consecuencia, se tendrá una probaribilidad del $95.8\%$, de que la mayoría apruebe realizar el proyecto de inversión.
En esta ocasión estamos interesados en calcular el número promedio y desviación estándar del número miembros que asistieron a la junta de votación y están a favor de realizar el proyecto de inversión, entonces al aplicar la ecuación de la media de la distribución hipergeométrica se tendrá que \[\begin{align*} \mathbb{E}(X) &=n\frac{M}{N} \\ &= 9 \left(\frac{10}{15}\right) \\ &= 6 \end{align*}\] Procedimiento similar se emplea para el cálculo de la varianza, en donde al aplicar la ecuación de la distribución hipergeométrica para la varianza, se tendrá que \[\begin{align*} Var(X)&=\left(\frac{N-n}{N-1}\right)\left(\frac{M}{N}\right)\left(1-\frac{M}{N}\right) \\ &=\left(\frac{15-9}{15-1}\right)\left(\frac{10}{15}\right)\left(1-\frac{10}{15}\right) \\ &= 0.0952381 \end{align*}\] Y con este valor, se realizar el cálculo de la desviación estándar, mediante la ecuación \[\begin{align*} Sd(X) &= \sqrt{Var(X)} \\ &= \sqrt{0.0952381} \\ &= 0.3086067 \end{align*}\] lo cual quiere decir que de los $9$ miembros que asistieron a la junta de votación, se espera que $6$ de ellos hayan votado a favor de llevar a cabo el proyecto de inversión, con una desviación estándar de $0.3086067$ miembros.

Experimento Binomial Negativo

Consideremos un experimento con las mismas propiedades de un experimento binomial, solo que en este caso, las pruebas se repetirán hasta que ocurra un número fijo de éxitos. Por lo tanto en vez de encontrar la probabilidad de $X$ éxitos en $n$ pruebas, donde $n$ es fija, ahora nos interesa la probabilidad de que ocurra el $k$ -ésimo éxito en la $X$ -ésima prueba.

Ejemplo

Los siguientes, son algunos ejemplos de casos que pueden considerarse Experimentos Binomial Negativo, debido a que cumplen las propiedades de un experimento binomial, es decir, las $4$ condiciones propuestas en el Proceso Bernoulli.

El número de inversionistas a los que hay que preguntarle si están a favor de un proyecto hasta encontrar el quinto que la apoye.
Revisar el número de metas alcanzadas en un proyecto hasta enontra la primera que no se ha complido.
Encuestar a un grupo de trabajadores de un proyecto hasta encontrar a la duodécima mujer.

Distribución Binomial Negativa

Sea $X$ el número de ensayos necesarios para generar $k$ éxitos en un experimento Binomial Negativo, entonces se dice que $X\sim b^*(k,p)$ si su función de probabilidad es de la forma \begin{align*} p(x) = \left(\begin{array}{c}x-1\\ k-1\end{array}\right)p^k(1-p)^{x-k} \quad \quad x=k, k+1, \ldots \end{align*}

En Excel, pueden calcularse probabilidades Binomiales Negativas mediante la función NEGBINOM.DIST() con $\text{núm_fracasos} = x-k$ y $\text{núm_éxitos} = k$ .

Media y Varianza Binomial Negativa

Si $X\sim b^*(k,p)$ , entonces se puede probar que la media y varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X)=\frac{k}{p} \quad \quad Var(X)=k\frac{(1-p)}{p^2} \end{align*}

Ejercicio

Suponga que por experiencia se sabe que $4$ de cada $5$ edificios construidos por una constructora famosa superan los estándares de calidad. Entonces basados en lo anterior,

Cuál es la probabilidad de que más de deban revisarse más de $3$ edificios construidos por dicha constructora hasta encontrar el segundo que no cumpla los estándares de calidad.
Cuál es el número promedio y desviación estándar del número de edificios que hay que revisar hasta encontrar el segundo edificio que no cumpla los estándares de calidad.

Solución

En este caso nos preguntan, por la probabilidad de que más de $3$ edificios construidos por dicha constructora hasta encontrar el primero que no cumpla los estándares de calidad, esto es \[\begin{align*} \mathbb{P}(X>3) \end{align*}\] Donde $X$: representa el número de edificios que no cumplen los estándares de calidad. Entonces, como estamos en una situación en la cual nos preguntan por el número de ensayos que hay que realizar, hasta obtener $1$ éxito, estamos en una situación asociada a una distribución Binomial Negativa, la cual tiene la estructura \[\begin{align*} p(x) = \left(\begin{array}{c}x-1\\ k-1\end{array}\right)p^k(1-p)^{x-k} \quad \quad x=k, k+1, \ldots \end{align*}\] En donde se sabe por experiencia que $4$ de cada $5$ edificios construidos por dicha constructora cumple los estándares de calidad, y por tanto, como nuestro éxito está asociado a que no se cumplan los estándares de calidad, se tendrá que $1$ de cada $5$ edificios no cumple dichos estándares, es decir que al aplicar la definición de frecuencia relativa, tendremos que la proporción $p$ de interés, estará dada por \[\begin{align*} p &= \frac{\text{# éxitos}}{\text{total Ensayos}} \\ &= \frac{1}{5} \\ &= 0.20 \end{align*}\] Ahora, al emplear la función de distribución Binomial Negativa con $p=0.20$, y con $k=2$ debido a que estamos interesados en el segundo edificio, tendremos que la probabilidad de interés estará dada por \[\begin{align*} \mathbb{P}(X>3) &= 1 - \mathbb{P}(X\leq 3) \\ &= 1 - \sum_{x=2}^3 \left(\begin{array}{c}x-1\\ 2-1\end{array}\right)0.20(1-0.20)^{x-1} \\ &= 1 - (0.04 + 0.064) \\ &= 1 - 0.104 \\ &= 0.896 \end{align*}\] En consecuencia, se tendrá un $89.6\%$ de probabilidad, de que deban revisarse más de $3$ edificios construidos por la constructora hasta encontrar el segundo que no cumpla los estándares de calidad.
En esta ocasión estamos interesados en conocer el número promedio y desviación estándar del número de edificios que hay que revisar hasta encontrar el segundo edificio que no cumpla los estándares de calidad. Y para ello podemos emplear la formula de la esperanza matemática, de la distribución Geométrica para realiza el cálculo, tal que \[\begin{align*} \mathbb{E}(X) &= \frac{k}{p} \\ &= \frac{2}{0.20}\\ &= 10 \end{align*}\] lo cual significa, que en promedio deberán revisar 10$ edificios construidos por la constructora famosa, hasta encontrar el segundo que no cumple los estándares de calidad.

Ahora, para completar la interpretación anterior, realizaremos el cálculo de la Varianza para el caso de una distribución Geométrica, tal que \[\begin{align*} Var(X) &= k\frac{(1-p)}{p^2} \\ &= 2\frac{1-0.2}{0.2^2} \\ &= 40 \end{align*}\] y con este valor se realiza el cálculo de la desviación estándar, mediante la ecuación \[\begin{align*} Sd(X) &= \sqrt{Var(X)} \\ &= \sqrt{40} \\ &= 6.324555 \end{align*}\] Y por tanto se tendrá que en promedio deberán revisar $10$ edificios construidos por la constructora famosa, hasta encontrar el segundo que no cumple los estándares de calidad, con una desviación estándar de $6.324555$ edificios.

Proceso Poisson

Un proceso Poisson es aquel que cumple

El número de resultados que ocurren en un intervalo o región específica es independiente del número que ocurre en cualquier otro intervalo de tiempo o región del espacio disjunto.
La probabilidad de que ocurra un solo resultado durante un intervalo de tiempo corto o región pequeña es proporcional a la longitud del intervalo o al tamaño de la región, y no depende del número de resultados que ocurren por fuera de este intervalo de tiempo o región.
La probabilidad de que ocurra más de un resultado en tal intervalo o región pequeña es insignificante.

Ejemplo

El número de automóviles que transitan por una avenida principal en dos horas.
El número de conductores que exceden los límites de velocidad por día.
El número de proyectos socioeconómicos que impulsa una alcaldía en un año.

Distribución Poisson

El número de sucesos que ocurren en un intervalo de tiempo o región específica, es una variable aleatoria $X$ con distribución de probabilidad Poisson, tal que \begin{align*} f(x) = \frac{e^{-\lambda}\lambda^x}{x!} \quad \quad x=0,1,\ldots \end{align*} donde $\lambda$ es el parámetro de la distribución y representa el número promedio de sucesos por unidad de tiempo o región específica.

En Excel, pueden calcularse probabilidades Poisson mediante la función POISSON.DIST().

Media y Varianza Poisson

Si $X\sim P(\lambda)$ entonces se puede probar que la media y varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X)=\lambda \quad \quad Var(X)=\lambda \end{align*}

Ejercicio

Los huecos en las carreteras pueden ser un problema grave y requieren de reparación constante con un tipo específico de mezcla de concreto. La experiencia sugiere que hay en promedio $1.5$ huecos por cada dos kilómetros recorridos, después de cierta cantidad de uso. Si se supone que $X$ representa el número de huecos que hay en la carretera

Cuál es la probabilidad de que no aparezca más de un hueco en la carretera en un tramo de dos kilómetros?
Cuál es la probabilidad de que aparezca más de hueco en un tramo de un kilómetro?
Cuál es el número promedio y desviación estándar del número de huecos que se encuentran en $5$ kilómetros?.

Solución

En este caso nos dicen que nuestra variable aleatorias es $X$ el número de huecos que se encuentran en la carretera, y que en promedio se encuentran $1.5$ huecos cada dos kilómetros.

Basados en lo anterior, nos preguntan por la probabilidad de que no aparezca más de un hueco en la carretera en un tramo de dos kilómetros. Es decir, nos preguntan por la probabilidad de que aparezca como máximo $1$ hueco en la carretera en un tramo de dos kilómetros. En este caso se tendrá la siguiente probabilidad \[\begin{align*} P(X\leq 1) &= \sum_{x=0}^1 \frac{e^{-1.5}1.5^x}{x!} \\ &= \frac{e^{-1.5}1.5^0}{0!} + \frac{e^{-1.5}1.5^1}{1!} \\\\ &= 0.2231302 + 0.3346952 \\ &= 0.5578254 \end{align*}\] Es decir, la probabilidad de que no aparezca más de un hueco en la carretera en el tramo de dos kilómetros es del $55.78\%$.
Ahora, se tiene interés en conocer la probabilidad de que aparezca más de un hueco en un tramo de un kilómetro. En este caso debe notarse que se cambió la unidad de medida, en donde en lugar de dos kilómetros se habla de un kilómetro.

Debido a ésto, será necesario actualizar nuestro parámetro $\lambda$ mediante el empleo de una regla de $3$, de la siguiente manera. \[\begin{align*} 2_{\text{km}} &- 1.5_{\text{huecos}} \\ 1_{\text{km}} &- \lambda \end{align*}\] esto es, \[\begin{align*} \lambda &= \frac{1.5_{\text{huecos}} \times 1_{\text{km}}}{2_{\text{km}}} \\ \lambda &= 0.75_{\text{huecos}} \end{align*}\] Es decir, que en un tramo de un kilómetro ocurren $0.75$ huecos en promedio. Conocido el valor del parámetro $\lambda$ para el tramo de un kilómetro, se procede a calcular la probabilidad de que aparezca más de un hueco en el tramo de un kilómetro, tal que \[\begin{align*} \mathbb{P}(X>1) = \sum_{x=2}^\infty \frac{e^{-0.75}0.75^x}{x!} \\ \end{align*}\] En donde se aprecia que es una suma infinita, y en consecuencia se procede a trabajar tal probabilidad por su complemento. \[\begin{align*} \mathbb{P}(X>1) &= 1 - \mathbb{P}(X\leq1) \\ &= 1 - \sum_{x=0}^1 \frac{e^{-0.75}0.75^x}{x!} \\ &= 1 - \frac{e^{-0.75}0.75^0}{0!} - \frac{e^{-0.75}0.75^1}{1!} \\ &= 1 - 0.4723666 - 0.3542749 \\ &= 0.1733585 \end{align*}\] Es decir que, la probabilidad de que se encuentre más de $1$ hueco en un tramo de $1$ kilómetro cuando se viaja por carretera, es del $17.33\%$.
Finalmente, se tiene interés en conocer cual será el promedio y desviación estándar, del número de huecos que se encontrarán en la carretera en el tramo de $5$ kilómetro. En este caso, como se cambia la unidad de medida de $2$ kilómetros a $5$ kilómetros, será necesario recalcular el valor de $\lambda$, ta que \[\begin{align*} 2_{\text{km}} &- 1.5_{\text{huecos}} \\ 5_{\text{km}} &- \lambda \end{align*}\] esto es, \[\begin{align*} \lambda &= \frac{1.5_{\text{huecos}} \times 5_{\text{km}}}{2_{\text{km}}} \\ \lambda &= 3.75_{\text{huecos}} \end{align*}\] Ahora, al aplicar la formular de esperanza matemática para la distribución Poisson, se tiene que el número esperado de huecos en $5$ kilómetros es de \[\begin{align*} \mathbb{E}(X) & = \lambda \\ & = 3.75\\ \end{align*}\] Similarmente, se procede a realizar el cálculo de la varianza para poder calcular la desviación estándar, del número de huecos que hay en un tramo de $5$ kilómetros \[\begin{align*} Var(X) &= \lambda \\ &= 3.75\\ \end{align*}\] y con este valor, se procede a calcular la desviación estándar \[\begin{align*} Sd(X) &= \sqrt{Var(X)} \\ &= \sqrt{Var(3.75)} \\ Sd(X) & = 1.936492 \end{align*}\] De lo anterior se tiene que, en el tramo de $5$ kilómetros de carretera, se espera encontrar $3.75$ huecos, con una desviación estándar de $1.93$ huecos.

Distribución de probabilidad continua

La función $f(x)$ es una función de densidad de probabilidad (fdp) para la variable aleatoria continua $X$ , definida en el conjunto de números reales, si

$f(x)\geq0$ para todo $x\in \mathbb R$
$\int_{-\infty}^\infty f(x)dx=1$
$P(a<x<b) = \int_a^b f(x)dx$ con $a$ y $b$ dos constantes $\in \mathbb{R}$

Ejercicio

Suponga que las ventas realizada por una compañía gaseosas, en millones de pesos por mes, es una variable aleatoria continua con función de probabilidad dada por \[\begin{align*} f(x)=\frac{1}{12}e^{\frac{-x}{12}} \quad \quad x>0 \end{align*}\] siendo $X$ una variable aleatoria que representa las ventas realizadas en un mes en millones de pesos. A partir de dicha función

Verifique si la función de densidad de probabilidad está bien definida? De no estarlo, multiplique la función por una constante $k$ para que quede bien definida.
Calcule la probabilidad de que en un mes se venda como máximo $8.3$ millones de pesos.

Solución

Para verificar si la función está bien definida, es necesario en primer lugar observar si para todo $X$ en el dominio definido, la función de probabilidad de densidad de probabilidad es mayor o igual a $0$. Para ello supongamos $3$ números diferentes, $0.1$ $10$ y $300$, los cuales vamos a evaluar en la función de densidad. \[\begin{align*} f(0.1) &= \frac{1}{12}e^{\frac{-0.1}{12}}=0.08264177 \\ f(10) &= \frac{1}{12}e^{\frac{-10}{12}}=0.03621652 \\ f(300) &= \frac{1}{12}e^{\frac{-300}{12}}=0.000000000001157329 \end{align*}\] Evidenciando que para todo $x>0$, $f(x)\geq0$.
En segundo lugar, para observar si la función de densidad de probabilidad está bien definida, es necesario observar si al integrar dicha función su resultado es igual a $1$, es decir, \[\begin{align*} \int_{-\infty}^\infty f(x)dx & = \int_{-\infty}^0 0\; dx + \int_{0}^\infty \frac{1}{12}e^{\frac{-x}{12}} dx \\ & =\int_{0}^\infty \frac{1}{12}e^{\frac{-x}{12}} dx \\ & = \frac{1}{12}\int_{0}^\infty e^{\frac{-x}{12}} dx \\ & = \frac{1}{12} \left[-12e^{\frac{-x}{12}}\right]\Bigg|_{0}^\infty \\ & = \left[-e^{\frac{-\infty}{12}} + e^{\frac{-0}{12}}\right] \\ & = -0 + 1 \\ & = 1 \end{align*}\] Entonces, como la integral da exactamente $1$, se tendrá que la función de densidad está bien definida.
Ahora, como estamos interesados en calcular la probabilidad de que en un mes se venda como máximo $8.3$ millones de pesos, tendremos que calcular \[\begin{align*} \mathbb{P}(X \leq 8.3) &= \int_{0}^{8.3} \frac{1}{12}e^{\frac{-x}{12}} dx \\ &= \frac{1}{12} \int_{0}^{8.3} e^{\frac{-x}{12}} dx \\ & = \frac{1}{12} \left[-12e^{\frac{-x}{12}}\right]\Bigg|_{0}^{8.3} \\ & = \left[-e^{\frac{-8.3}{12}} + e^{\frac{-0}{12}}\right] \\ & = -0.5007408 + 1 \\ & = 0.4992592 \end{align*}\] En consecuencia, se tendrá una probabilidad del $49.93\%$ de que en un mes esta empresa se venda como máximo $8.3$ millones de pesos.

Función de distribución acumulada caso continuo

La función de distribución acumulada (fda) denotada por $F(x)$ , para una variable aleatoria continua $X$ con distribución de densidad de probabilidad $f(x)$ es de la forma \begin{align*} F(x)=P(X\leq x)=\int_{-\infty}^x f(t)dt \quad \quad -\infty<x<\infty \end{align*} para cualquier $x$ , $F(x)$ es el área bajo la curva de densidad a la izquierda de valor que tome $x$ .

Nota: Si se quieren calcular probabilidades con la función de distribución acumulada en el caso continuo, entonces, si $a$ y $b$ son dos números constantes, deberán tenerse en cuenta las siguientes reglas

$\mathbb{P}(a \leq X \leq b) = \mathbb{P}(X \leq b) - \mathbb{P}(X - a)$
$\mathbb{P}(X \geq a) = 1 - \mathbb{P}(X < a)$
$\mathbb{P}(X > a) = 1 - \mathbb{P}(X \leq a)$
$\mathbb{P}(X \leq b) = F(b)$
$\mathbb{P}(X < b) = F(b)$

Nota: Recordar que en el caso continuo, las probabilidad con o sin la igualdad son equivalentes, y por tanto, solo se escriben las tres reglas anteriores para generalizar todos los casos.

Ejercicio

Calcule la función de distribución acumulada $F(x)$.
Calcule la probabilidad de que en un mes se venda como mínimo $16$ millones de pesos.

Solución

Para encontrar la función de distribución acumulada a partir de una función de densidad de probabilidad, es necesario realizar la integral de la función de densidad, de la forma \[\begin{align*} F(x)& = \int_{-\infty}^x f(t)dt \\ & = \int_{-\infty}^0 0dt + \int_{0}^x \frac{1}{12}e^{\frac{-t}{12}} dt \\ & = \int_{0}^x \frac{1}{12}e^{\frac{-t}{12}} dt \\ & = \frac{1}{12} \left[-12e^{\frac{-t}{12}}\right]\Bigg|_{0}^{x} \\ & = \left[-e^{\frac{-x}{12}} + e^{\frac{-0}{12}}\right] \\ & = - e^{\frac{-x}{12}} + 1 \\ & = 1 - e^{\frac{-x}{12}} \end{align*}\]
Dado que el interés es calcular la probabilidad de que en un mes se venda como mínimo $16$ millones de pesos, entonces se tendrá que la probabilidad de interés, es la siguiente \[\begin{align*} \mathbb{P}(X \geq 16) \end{align*}\] Entonces, siguiendo las reglas anteriormente expuestas para calcular probabilidad con la función de distribución acumulada continua, se tendrá que \[\begin{align*} \mathbb{P}(X \geq 16) &= 1 - F(16) \\ &= 1 - \left(1 - e^{\frac{-16}{12}}\right) \\ &= e^{\frac{-16}{12}} \\ &= 0.2635971 \end{align*}\] y por tanto, se tendrá que la probabilidad de que en un mes se venda como mínimo $16$ millones de pesos es del $26.36\%$.

Algunas distribuciones de probabilidad continua

Distribución Uniforme Continua

Se dice que la variable aleatoria $X$ tiene una distribución uniforme continua, definida en el intervalo $(a,b)$ , si su función de probabilidad está dada por \begin{align*} f(x) = \begin{cases} \frac{1}{b-a} \quad \quad & a\leq x\leq b \\ 0 \quad \quad & \text{en otro caso}\end{cases} \end{align*}

Media y Varianza Uniforme Continua

Si $X\sim Unif(a,b)$ , entonces se puede probar que la media y varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X) = \frac{b+a}{2} \quad \quad Var(X)=\frac{(b-a)^2}{12} \end{align*}

Distribución Acumulada Uniforme Continua

Si $X\sim Unif(a,b)$ , entonces se puede probar que la función de distribución acumulada de la variable aleatoria $X$ es de la forma \begin{align*} F(x) = \frac{x-a}{b-a} \quad \quad & a\leq x\leq b \end{align*}

Ejercicio

Suponga que el tiempo máximo que se puede reservar una sala de conferencias grande en cierta empresa son cuatro horas. Por experiencia se sabe que la sala es reservada con mucha frecuencia, tanto para conferencias extensas como para conferencias breves, de hecho, se puede suponer que la duración $X$ de una conferencia tiene una distribución uniforme en horas en el intervalo $[0, 4]$. Basado en lo anterior

Calcule la función de densidad de probabilidad $f(x)$ y la función de distribución acumulada $F(X)$ para el tiempo que dura una conferencia.
Cuál es la probabilidad de que una conferencia dure menos de $2$ horas?
Si una conferencia lleva más de $2$ horas, cuál es la probabilidad de que dure a lo más $3$ horas?
Cuál es el tiempo medio y la desviación estándar de la duración de una conferencia?

Solución

Del enunciado anterior, se menciona que la duración de las conferencias sigue una distribución uniforme con límite mínimo $a=0$, y límite máximo $b=4$, y por tanto, se tendrá que la función de densidad de probabilidad estará dada por \[\begin{align*} f(x) = \frac{1}{4-0} = \frac{1}{4} \quad \text{ para } 0\leq x\leq 4 \end{align*}\] Ahora, al calcular la función de distribución acumulada se tendrá que \[\begin{align*} F(x) = \frac{x-0}{4-a} = \frac{x}{4} \quad \text{ para } 0\leq x\leq 4 \end{align*}\]
En este punto estamos interesados en calcular la probabilidad de que una conferencia dure menos de $2$ horas, es decir, estamos interesados en calcular \[\begin{align*} \mathbb{P}(X<2) \end{align*}\] en donde, al estar en una situación de una distribución continua, se tendrá que la probabilidad planteada es equivalente a \[\begin{align*} \mathbb{P}(X<2) = \mathbb{P}(X \leq 2) \end{align*}\] y por tanto, al emplear la función de distribución acumulada $F(X)=\mathbb{P}(X\leq x)$ se tendrá que \[\begin{align*} \mathbb{P}(X<2) &= F(2) \\ &= \frac{2}{4} \\ &= \frac{1}{2} \\ &= 0.5 \end{align*}\] Y por tanto se tendrá una probabilidad del $50\%$ de que una conferencia en particular tarde menos de $2$ horas.
A diferencia del caso anterior, en éste punto estamos interesados en calcular una probabilidad condicional, en donde nos piden la probabilidad de que una conferencia dure como máximo $3$ horas, cuando se sabe que ésta conferencia ya lleva más de $2$ horas y aún no termina, es decir \[\begin{align*} \mathbb{P}(X\leq 3 | X>2) \end{align*}\] entonces, al aplicar la definición de probabilidad condicional, tendremos que \[\begin{align*} \mathbb{P}(X\leq 3 | X>2) &= \frac{\mathbb{P}(X\leq 3 \cap X>2)}{\mathbb{P}(X>2)} \\ &= \frac{\mathbb{P}(2 \leq X\leq 3)}{1 - \mathbb{P}(X\leq 2)} \\ &= \frac{\mathbb{P}(X\leq 3) - \mathbb{P}(X\leq 2)}{1 - \mathbb{P}(X\leq 2)} \\ \end{align*}\] Ahora, al aplicar la función de distribución acumulada $F(X)=\mathbb{P}(X\leq x)$ se tendrá que \[\begin{align*} \mathbb{P}(X\leq 3 | X>2) &= \frac{\mathbb{P}(X\leq 3) - \mathbb{P}(X\leq 2)}{1 - \mathbb{P}(X\leq 2)} \\ &= \frac{F(3) - F(2)}{1 - F(2)} \\ &=\frac{\frac{3-0}{4-0} - \frac{2-0}{4-0}}{1 - \frac{2-0}{4-0}} \\ &=\frac{\frac{3}{4} - \frac{2}{4}}{1 - \frac{2}{4}} \\ &=\frac{\frac{1}{4}}{\frac{2}{4}} \\ &= \frac{1}{2} \\ &= 0.5 \end{align*}\] Y en consecuencia, se tendrá que si una conferencia ha durado más de $2$ horas y aún no termina, la probabilidad de que cure como máximo $3$ horas es de $50\%$.
Finalmente, estamos interesados en calcular el promedio y desviación estándar, del número de horas que se reserva la sala de conferencias, y como, la distribución de probabilidad asociada a la variable aleatoria es una uniforme, tendremos que la media de la distribución estará dada por \[\begin{align*} \mathbb{E}(X) &= \frac{4+0}{2} \\ &= \frac{4}{2} \\ &= 2 \end{align*}\] mientras que la varianza estará dada por \[\begin{align*} Var(X) &= \frac{(4-0)^2}{12} \\ &= \frac{4^2}{12} \\ &= \frac{16}{12} \\ &= 1.33333 \end{align*}\] En donde, dada la relación de la varianza con la desviación estándar, tendremos que \[\begin{align*} Sd(X) &= \sqrt{Var(X)}\\ &= \sqrt{1.33333}\\ &= 1.154699 \end{align*}\] Por lo cual tendremos que, el número promedio de horas que se reserva la sala de conferencias es de $2$ horas, con una desviación estándar de $1.15$ horas.

Distribución Gamma

Se dice que la variable aleatoria $X$ tiene una distribución Gamma con parámetro de forma $\alpha$ y de escala $\beta$ , si su función de densidad de probabilidad está dada por \begin{align*} f(x) = \begin{cases} \frac{1}{\Gamma(\alpha)\beta^\alpha} x^{\alpha-1}e^{-{\frac{x}{\beta}}} \quad \quad & x>0; \alpha>0; \beta>0 \\ 0 \quad \quad & \text{en otro caso}\end{cases} \end{align*}

En Excel, pueden calcularse probabilidades Gamma mediante la función DISTR.GAMMA.N().

Media y Varianza Gamma

Si $X\sim Gamma(\alpha,\beta)$ , entonces se puede probar que la media y varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X) = \alpha\beta \quad \quad Var(X)=\alpha\beta^2 \end{align*}

Ejercicio

Suponga que se realiza un estudio sobre el tiempo de transferencia de datos de un sistema de red informática, en milisegundos. Si se encuentra que el tiempo de transferencia se distribuye gamma con parámetro de forma igual a $3_{ms}$ y parámetro de escala igual a $\frac{37}{3}$. Basados en lo anterior, Cual es la probabilidad de que el tiempo de transferencia de datos exceda $50_{ms}$?

Solución

Basados en los parámetros de forma y escala, estamos interesados en calcular la probabilidad de que el tiempo de transferencia de datos exceda los $50_{ms}$, es decir \[\begin{align*} \mathbb{P}(X>50) \end{align*}\] la cual, al emplear la distribución $Gamma(\alpha=3, \beta=37/3)$ se tendrá que \[\begin{align*} \mathbb{P}(X>50) &= \int_{50}^{\infty} \frac{1}{\Gamma(\alpha)\beta^\alpha} x^{\alpha-1}e^{-{\frac{x}{\beta}}} dx \\ &= \int_{50}^{\infty} \frac{1}{\Gamma(3)(37/3)^3} x^{3-1}e^{-{\frac{x}{(37/3)}}} dx \\ &= \frac{3^3}{\Gamma(3)(37)^3}\int_{50}^{\infty} x^{2}e^{-{\frac{3x}{37}}} dx \end{align*}\] En donde para calcular tan integral debemos realizar integración por partes dos veces, debido a que el parámetro $\alpha=3$, tal que \[\begin{align*} \mathbb{P}(X>50) &= \frac{3^3}{\Gamma(3)(37)^3}\int_{50}^{\infty} x^{2}e^{-{\frac{3x}{37}}} dx\\ &=> u=x^2 \quad \quad \; dv = e^{-{\frac{3x}{37}}} dx \\ &=> du= 2x dx \quad v = - \frac{37}{3} e^{-{\frac{3x}{37}}} \\ &= \frac{3^3}{\Gamma(3)(37)^3} \left[-\frac{37}{3}x^2 e^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty + \frac{(2)(37)}{3}\int_{50}^{\infty} xe^{-{\frac{3x}{37}}} dx\right] \\ &=> u=x \quad \quad \; dv = e^{-{\frac{3x}{37}}} dx \\ &=> du= dx \quad v = - \frac{37}{3} e^{-{\frac{3x}{37}}} \\ &= \frac{3^3}{\Gamma(3)(37)^3} \left[-\frac{37}{3}x^2 e^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty + \frac{(2)(37)}{3} \left\{-\frac{37}{3}x e^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty+ \frac{37}{3} \int_{50}^\infty e^{-{\frac{3x}{37}}}dx\right\} \right] \\ &= \frac{3^3}{\Gamma(3)(37)^3} \left[-\frac{37}{3}x^2 e^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty + \frac{(2)(37)}{3} \left\{-\frac{37}{3} xe^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty - \frac{37^2}{3^2} e^{-{\frac{3x}{37}}}\Bigg|_{50}^\infty\right\} \right] \\ &= \frac{3^3}{\Gamma(3)(37)^3} \left[-\frac{37}{3}x^2 e^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty -\frac{(2)(37^2)x}{3^2} e^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty - \frac{(2)(37^3)}{3^3} e^{-{\frac{3x}{37}}}\Bigg|_{50}^\infty \right] \\ &= \frac{3^3}{\Gamma(3)(37)^3} \left[-\frac{37}{3}x^2 e^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty -\frac{(2)(37^2)}{3^2} xe^{-{\frac{3x}{37}}} \Bigg|_{50}^\infty - \frac{(2)(37^3)}{3^3} e^{-{\frac{3x}{37}}}\Bigg|_{50}^\infty \right] \\ &= \left(-\frac{3^2}{\Gamma(3)(37)^2}x^2 e^{-{\frac{3x}{37}}} - \frac{(2)(3)}{\Gamma(3)(37)} xe^{-{\frac{3x}{37}}} - \frac{(2)}{\Gamma(3)} e^{-{\frac{3x}{37}}}\right)\Bigg|_{50}^\infty \end{align*}\] Por tanto al evaluar la variable $x$ en los límites de interés tendremos que \[\begin{align*} \mathbb{P}(X>50) &= \left(-\frac{3^2}{\Gamma(3)(37)^2}x^2 e^{-{\frac{3x}{37}}} - \frac{(2)(3)}{\Gamma(3)(37)} xe^{-{\frac{3x}{37}}} - \frac{(2)}{\Gamma(3)} e^{-{\frac{3x}{37}}}\right)\Bigg|_{50}^\infty \\ &= \left(0 + 0 + 0 \right) - \left(-\frac{3^2}{\Gamma(3)(37)^2}(50^2) e^{-{\frac{3(50)}{37}}} - \frac{(2)(3)}{\Gamma(3)(37)} (50)e^{-{\frac{3(50)}{37}}} - \frac{(2)}{\Gamma(3)} e^{-{\frac{3(50)}{37}}}\right) \\ &= \frac{3^2}{\Gamma(3)(37)^2}(50^2) e^{-{\frac{3(50)}{37}}} + \frac{(2)(3)}{\Gamma(3)(37)} (50)e^{-{\frac{3(50)}{37}}} + \frac{(2)}{\Gamma(3)} e^{-{\frac{3(50)}{37}}} \\ &= 0.14259 + 0.07035 + 0.01735 \\ &= 0.23029 \end{align*}\] Es decir, que la probabilidad de que el tiempo de transferencia de datos exceda los $50_{ms}$, es del $23.029\%$.

Distribución Exponencial

Se dice que la variable aleatoria $X$ tiene una distribución Exponencial con parámetro de escala $\beta$ , si su función de densidad de probabilidad está dada por \begin{align*} f(x) = \begin{cases} \frac{1}{\beta} e^{-{\frac{x}{\beta}}} \quad \quad & x>0; \beta>0 \\ 0 \quad \quad & \text{en otro caso}\end{cases} \end{align*} en donde se observa que ésta distribución es un caso particular de la distribución Gamma cuando $\alpha=1$ .

En Excel, pueden calcularse probabilidades Exponencial mediante la función DISTR.EXP.N().

Media y Varianza Exponencial

Si $X\sim Exp(\beta)$ , entonces se puede probar que la media y varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X) = \beta \quad \quad Var(X)=\beta^2 \end{align*}

Distribución Acumulada Exponencial

Si $X\sim Exp(\beta)$ , entonces se puede probar que la función de distribución acumulada de la variable aleatoria $X$ es de la forma \begin{align*} F(x) = 1 - e^{-{\frac{x}{\beta}}} \quad \quad & x>0; \beta>0 \end{align*}

Ejercicio

Suponga que Bancolombia está interesado en saber si es necesario aumentar el número de cajeros que hay en una zona de la ciudad, y encuentra que el tiempo entre llegadas sucesiva de personas a un cajero de la zona, posee una distribución Exponencial con un tiempo promedio de $0.8$ minutos. Entonces, basados en ésto, calcule la probabilidad de que la próxima persona en llegar al cajero tarde más de $4$ minutos?

Solución

Para calcular la probabilidad de que la próxima persona tarde más de $4$ minutos en llegar al cajero, debemos primero encontrar el valor del parámetro de la distribución Exponencial, en donde, nos dicen en el enunciado, que el tiempo promedio entre llegadas sucesivas es de $0.8$ minutos, tal que \[\begin{align*} \mathbb{E}(X) &= 0.8 \end{align*}\] Entonces como para la distribución Exponencial se tiene que el valor de la esperanza matemática está dada por \[\begin{align*} \mathbb{E}(X) &= \beta \end{align*}\] se tendrá que el parámetro $\beta$ de la distribución Exponencial será igual a \[\begin{align*} \beta &= 0.8 \end{align*}\] Ahora, con el valor de este parámetro podemos calcular la probabilidad de interés empleando la función de distribución acumulada Exponencial, tal que \[\begin{align*} \mathbb{P}(X>4) &= 1 - \mathbb{P}(X\leq 4) \\ &= 1 - F(4) \\ &= 1 - \left(1 - e^{-{\frac{4}{\beta}}}\right) \\ &= 1 - \left(1 - e^{-{\frac{4}{0.8}}}\right) \\ &= e^{-{\frac{4}{3}}} \\ &= 0.006737947 \end{align*}\] Es decir que la probabilidad de que la próxima persona en llegar cajero de Bancolombia tarde más de $4$ minutos es de $0.67\%$.

Distribución Weibull

Se dice que la variable aleatoria $X$ tiene una distribución Weibull con parámetros $\alpha$ y $\beta$ , si su función de densidad de probabilidad es de la forma \begin{align*} f(x) = \begin{cases} \frac{\alpha}{\beta}\left(\frac{x}{\beta}\right)^{\alpha - 1}e^{-\left(\frac{x}{\beta}\right)^\alpha} & x\geq 0, \alpha>0, \beta>0 \\ 0 & \text{en otro caso} \end{cases} \end{align*}

donde, $\alpha$ se conoce como el parámetro de forma y $\beta$ como el parámetro de escala. Además, si $\alpha=1$ se tendrá que la distribución Weibull será igual a la distribución Exponencial.

En Excel, pueden calcularse probabilidades Weibull mediante la función DISTR.WEIBULL().

Media y Varianza Weibull

Si $X\sim Wei(\alpha, \beta)$ , entonces se puede probar que la media y la varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X)=\beta\;\Gamma\left(1 + \frac{1}{\alpha}\right) \quad \quad Var(X)=\beta^2\left[\Gamma\left(1 + \frac{2}{\alpha}\right) - \Gamma\left(1 + \frac{1}{\alpha}\right)^2\right] \end{align*}

Función de distribución acumulada Weibull

Si $X\sim Wei(\alpha, \beta)$ , entonces se puede probar que la función de distribución acumulada de $X$ está dada por \begin{align*} F(x) = \mathbb{P}(X\leq x) = \begin{cases} 0 & x<0 \\ 1- e^{-\left(\frac{x}{\beta}\right)^\alpha} & x\geq 0 \end{cases} \end{align*}

Ejercicio

Un ingeniero industrial realiza un estudio sobre la vida útil, en años, de un nuevo aire acondicionado que fabrican en la compañía donde trabaja, y luego de probar muchos aires, encontró que el tiempo de vida, en años, se distribuye Weibull con parámetros $\alpha=2$ y $\beta = 8$. Dado lo anterior, cuál es la probabilidad de que un aire acondicionado falle después de $3$ años de uso?

Solución

En el enunciado del ejercicio nos dicen tanto la distribución de la vida útil del aire acondicionado, y los parámetros de la distribución, tal que, $X \sim Wei(\alpha=2,\beta=8)$. Adicionalmente, estamos interesados en calcular la probabilidad de que el aire acondicionado falle después de $3$, es decir, que la vida útil supere los $3$ años. Esto es \[\begin{align*} \mathbb{P}(X>3) = \int_3^\infty \frac{2}{8}\left(\frac{x}{8}\right)^{2 - 1}e^{-\left(\frac{x}{8}\right)^2} dx \end{align*}\] Al hacer cambio de variable tenemos que \[\begin{align*} u= \left(\frac{x}{8}\right)^2 \quad \quad du = \frac{2}{8}\left(\frac{x}{8}\right)^{2-1} dx \end{align*}\] Entonces, al evaluar los límites de la integral debido al cambio de variable, se tiene que cuando $x=3$, el valor de $u=(3/8)^2$, y cuando $x=\infty$, el valor de $u=(\infty/8)^2 = \infty$. Por tanto, al hacer el cambio de variable y cambiar los límites de integración tenemos que \[\begin{align*} \mathbb{P}(X\geq3) &= \int_{\left(\frac{3}{8}\right)^2}^\infty e^{-u} du \\ &= -e^{-u} \Bigg|_{\left(\frac{3}{8}\right)^2}^\infty \\ &= -e^{-\infty} + e^{-\left(\frac{3}{8}\right)^2} \\ &= 0 + 0.8688151 \\ &= 0.8688151 \end{align*}\] Es decir, se tendrá una probabilidad del $86.88\%$ de que el aire acondicionado falle después de los $3$ años de uso.

Distribución Normal

Se dice que la variable aleatoria $X$ tiene una distribución Normal con parámetros $\mu$ y $\sigma^2)$ , si su función de densidad de probabilidad es de la forma \begin{align*} f(x) = \begin{cases} \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x - \mu)^2}{2\sigma^2}} & -\infty<x<\infty, -\infty<\mu<\infty, \sigma^2>0 \\ 0 & \text{en otro caso} \end{cases} \end{align*}

En Excel, pueden calcularse probabilidades Normales mediante la función DISTR.NORM.N().

Media y Varianza Normal

Si $X\sim N(\mu, \sigma^2)$ , entonces se puede probar que la media y la varianza de la variable aleatoria $X$ están dadas por \begin{align*} \mathbb{E}(X)=\mu \quad \quad Var(X)=\sigma^2 \end{align*}

Distribución Normal estándar

Un caso particular de la distribución normal cuando la media $\mu=0$ y ka varianza $\sigma^2=1$ , recibe el nombre de distribución normal estándar, cuya variable aleatoria se simboliza con $Z$ , tal que $Z\sim N(0,1)$ , y donde su función de densidad de probabilidad está dada por

\begin{align*} f(z) = \begin{cases} \frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}} & -\infty<z<\infty \\ 0 & \text{en otro caso} \end{cases} \end{align*}

En Excel, pueden calcularse probabilidades Normales estándar mediante la función DISTR.NORM.ESTAND.N().

Teorema de Estandarización

Si $X\sim N(\mu, \sigma^2)$ , siendo $a$ y $b$ dos constantes cualquiera, entonces si se realiza la transformación $Z=\frac{x-\mu}{\sigma}$ conocida como estandarización, se tendrá que $Z\sim N(0,1)$ , con $z_1$ y $z_2$ las dos constantes transformadas.

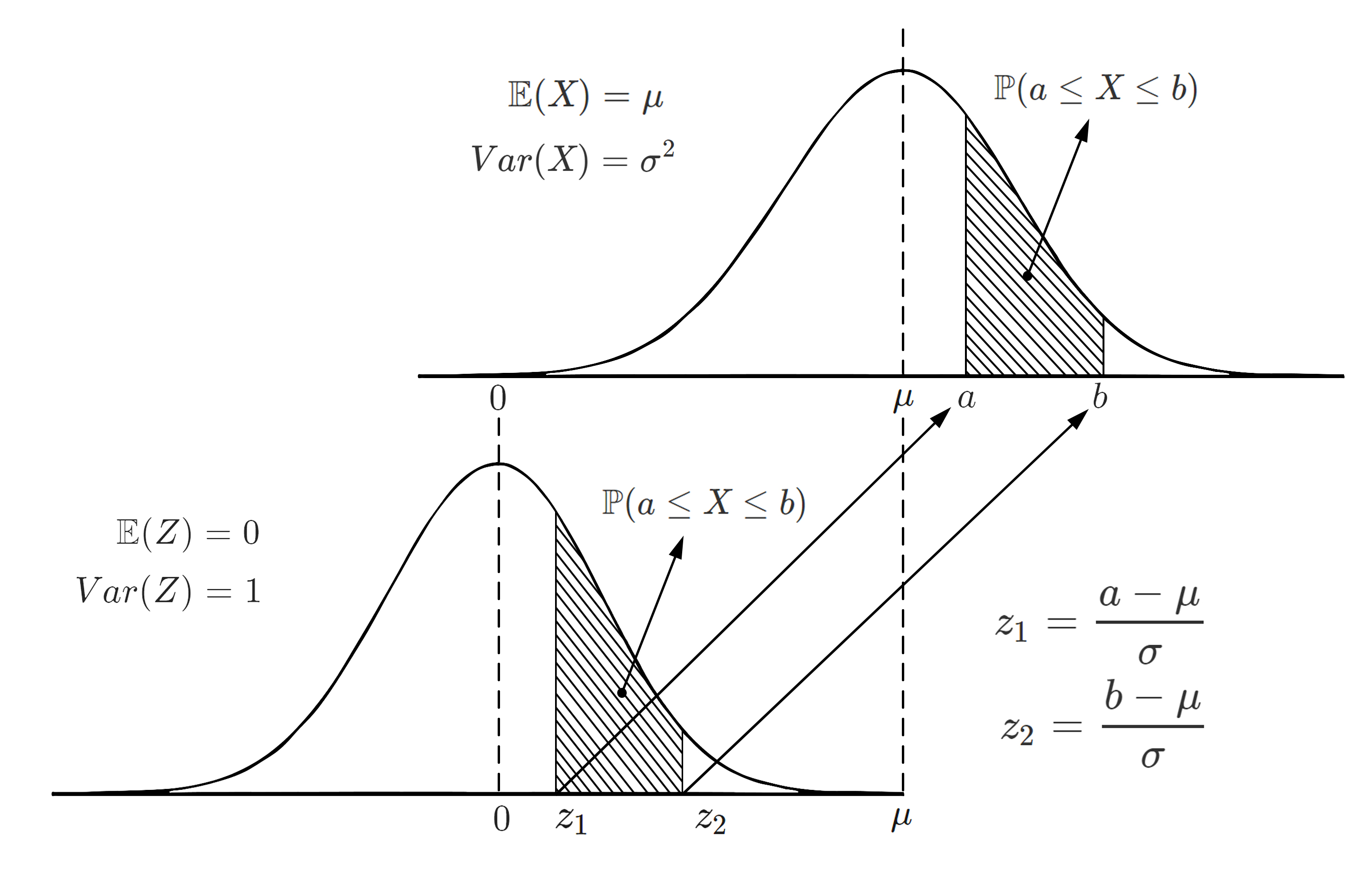
Propiedades

Si $X\sim N(\mu, \sigma^2)$ , entonces al aplicar el teorema de estandarización $Z=\frac{x-\mu}{\sigma} \sim N(0,1)$ , y por tanto, si $z_1$ y $z_2$ son constantes, se tendrá que

$\mathbb{P}(Z\leq z_1) = \mathbb{P}(Z\geq -z_1)$
$\mathbb{P}(Z\geq z_1) = \mathbb{P}(Z\leq -z_1) = 1- \mathbb{P}(Z\leq z_1)$
$\mathbb{P}(z_1\leq Z\leq z_2) = \mathbb{P}(Z\leq z_2) - \mathbb{P}(Z< z_1)$
Si $z_1 = - z_2$ entonces $\mathbb{P}(z_1\leq Z\leq z_2) = \mathbb{P}(-z_2\leq Z\leq z_2) =2\mathbb{P}(Z\leq z_2) - 1$
$Z_\alpha$ es el valor de la variable aleatoria $Z\sim N(0,1)$ tal que $\mathbb{P}(Z\geq Z_\alpha)=\alpha$ , y $\mathbb{P}(Z\leq Z_\alpha)=1 - \alpha$

En donde, debe recordarse que, al ser la distribución normal una distribución continua, la $\mathbb{P}(Z\leq z_1) = \mathbb{P}(Z< z_1)$ y $\mathbb{P}(Z\geq z_1) = \mathbb{P}(Z > z_1)$ . Lo anterior debido a que en la distribuciones continuas la probabilidad puntual es igual a $0$ .

Ejercicio

Suponga que cierto tipo de batería para celular dura en promedio $5$ años con una desviación estándar de $1.2$ años. Si se sabe por experiencia que la distribución de las baterías se distribuye normalmente, cuál es la probabilidad de que una batería de celular dure al menos $4$ años?

Solución

En este caso estamos interesados en que la batería de una celular dure al menos $4$ años, es decir, queremos calcular la siguiente probabilidad. \[\begin{align*} \mathbb{P}(X \geq 4) \end{align*}\] Pero en este caso tenemos que la distribución de los datos no se distribuye $N(0,1)$, si no que se distribuye $N(5, 1.2)$, y por ello debemos aplicar el teorema de estandarización, con el fin de llevar la distribución $N(5, 1.2)$ a una normal estándar, tal que \[\begin{align*} \mathbb{P}(X \geq 4)&=\mathbb{P}\left(\frac{X-\mu}{\sigma}\geq \frac{4-5}{1.2}\right)\\ \mathbb{P}(X \geq 4)&=\mathbb{P}\left(\frac{X-\mu}{\sigma}\geq \frac{4-5}{1.2}\right)\\ \mathbb{P}(X \geq 4)&=\mathbb{P}(Z \geq -0.83) \end{align*}\] En donde $Z\sim N(0,1)$. Ahora, como la estructura de la probabilidad de $Z$ no posee la estructura de la probabilidad de se maneja en la tabla, entonces procedemos a calcular el complemento de la probabilidad, tal que \[\begin{align*} \mathbb{P}(Z \geq -0.83)&= 1 - \mathbb{P}(Z < -0.83) \\ \end{align*}\] y en consecuencia podemos ahora buscar la probabilidad $\mathbb{P}(Z < -0.83)$ usando la función `DISTR.NORM.ESTAND.N()` de Excel, donde se aprecia que \[\begin{align*} \mathbb{P}(Z < -0.83)=0.2033 \end{align*}\] y por tanto, se tendrá que \[\begin{align*} \mathbb{P}(Z \geq -0.83)&= 1 - \mathbb{P}(Z < -0.83) \\ &= 1 - 0.2033 \\ &= 0.7967 \end{align*}\] lo cual es equivalente a \[\begin{align*} \mathbb{P}(X \geq 4)&= \mathbb{P}(Z \geq -0.83) \\ &= 0.7967 \end{align*}\] En consecuencia, se tendrá que la probabilidad de que una batería de celular dure al menos $4$ años, es del $76.67\%$.

\(X\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\text{ o más}\)
\(p(x)\)	\(0.0498\)	\(0.1494\)	\(0.2240\)	\(0.2240\)	\(0.1680\)	\(0.1848\)

\(X\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\text{ o más}\)
\(p(x)\)	\(0.0498\)	\(0.1494\)	\(0.2240\)	\(0.2240\)	\(0.1680\)	\(0.1848\)