Lista de ejercicios

  1. Suponga las siguientes series de tiempo suministradas en los archivos de los siguientes enlaces Serie 5, Serie 6, Serie 7, Serie 8, Serie 9, Serie 10, y con cada una de ellas
    1. Identifique mediante el gráfico de la serie y su ACF las componentes que posee la serie de tiempo.
    2. Para las series estacionarias en media, trate de identificar los órdenes \(p\) y \(q\) de los procesos \(AR\), \(MA\) o \(ARMA\).
    3. Escriba el modelo teórico para cada una de las series usadas en el inciso b.
    4. Para las series con tendencia, aplique la primera diferencia y trate de identificar los órdenes \(p\) y \(q\) de los procesos \(AR\), \(MA\) o \(ARMA\).
    5. Escriba el modelo teórico para cada una de las series usadas en el inciso d. 
    6. Para las series estacionales, aplique la \(s\)-ésima diferencia, y trate de identificar los órdenes \(p\) y \(q\), de los procesos \(AR\), \(MA\) o \(ARMA\).
    7. Escriba el modelo teórico para cada una de las series usadas en el inciso f. 
  2. A partir de las ecuaciones presentados a continuación, identifique el modelo y pruebe si los modelos propuestos son invertibles y/o estacionarios. Para todos los casos se asume que $\varepsilon \sim RB(0,\sigma)$
    1. \(Y_t = \varepsilon_t - 0.3\varepsilon_{t-1}\)
    2. \(Y_t = -0.54Y_{t-1} + \varepsilon_t\)
    3. \(Y_t = -1.79Y_{t-1} - 0.79Y_{t-2}+ \varepsilon_t\)
    4. \(Y_t = 0.31Y_{t-1} + 0.84Y_{t-2}+ \varepsilon_t + 0.51\varepsilon_{t-1}\)
    5. \(Y_t = 0.82Y_{t-1} + \varepsilon_t - 1.08\varepsilon_{t-1}\)
    6. \(Y_t = 2 - 0.51Y_{t-1} - 0.24Y_{t-2} + \varepsilon_t - 0.31\varepsilon_{t-1} + 1.49\varepsilon_{t-2}\).
    7. \(Y_t = -0.64Y_{t-2} + \varepsilon_t + 0.58\varepsilon_{t-1} + 1.20\varepsilon_{t-2}\)
    8. \(Y_t = Y_{t-1} + \varepsilon_t\)
    9. \(Y_t = 1.3Y_{t-1} + 0.3Y_{t-2} + \varepsilon_t + 2.32\varepsilon_{t-2}\)
    10. \(Y_t = -2Y_{t-1} -1 Y_{t-2} + \varepsilon_t - 0.46\varepsilon_{t-1}\)
  3. Realice los gráficos teóricos ACF y PACF que deberían tener un proceso
    1. \(MA(1)\)
    2. \(SMA(4)[6]\)
    3. \(AR(3)\)
    4. \(SMA(2)[3]\)
    5. \(ARMA(0,3)\)
    6. \(SARMA(2,1)[3]\)
    7. \(ARMA(3,1)\)
  4. A partir de las siguientes EACF, indique qué modelos creería usted que son plausibles para cada caso.
################### Caso 1 ###################

AR/MA
   0 1 2 3 4 5 6 7 8 9 10
0  x x o x x o o o o o o 
1  x x x x x o o o o o o 
2  x x x o o o o o o o o 
3  x o x o o o o o o o o 
4  x x x o o o o o o o o 
5  x x x o o o o o o o o 
6  x x x x o o o o o o o 
7  x x x x o o o o o o o 
8  x x x x o o o o o o o 
9  x x x o o x o o o o o 
10 x o o x x o o o o o o 

################### Caso 2 ###################

AR/MA
   0 1 2 3 4 5 6 7 8 9 10
0  x x x o x x x x x x x 
1  o x x o x o o o o o o 
2  o x x x x o o o o o o 
3  x o x x o x o o o o o 
4  o o x x o x o o o o o 
5  o x x x x x o o o o o 
6  o x x x o o o o o o o 
7  x o x x o o o x o o o 
8  x o x x x o o x o o o 
9  x x x x o o o x o o o 
10 x o x x o x o x o o o 

################### Caso 3 ###################

AR/MA
   0 1 2 3 4 5 6 7 8 9 10
0  x x x x x x x o o o o 
1  o o o o o o o o o o o 
2  x x o o o o o o o o o 
3  x o o o o o o o o o o 
4  x x o o o o o o o o o 
5  x x x o o o o o o o o 
6  x x x o o o o o o o o 
7  x o x o o o o o o o o 
8  x o x o o o x o o o o 
9  x x x x x x x o o o o 
10 x x x o o x o o o o o
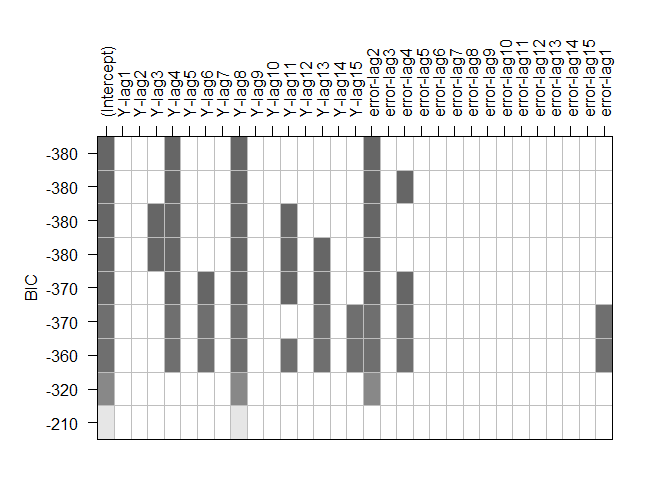
  1. A partir de los resultados obtenidos mediante la función $armasubsets()$ de la librería TSA del R, trate de identificar el modelo más plausibles para cada caso.
################### Caso 1 ###################

Reordering variables and trying again:


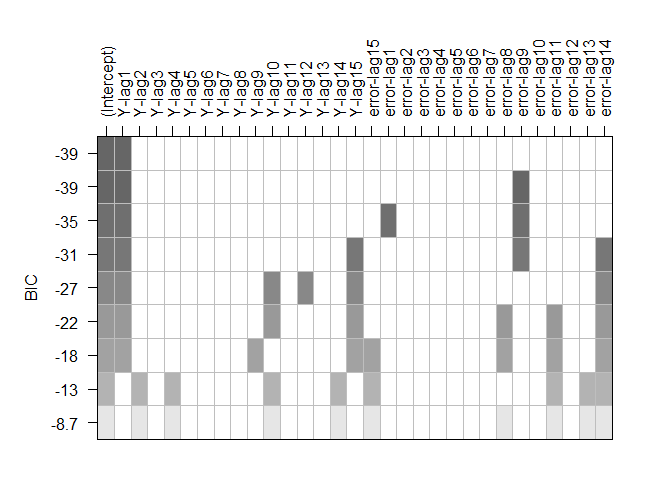
################### Caso 2 ###################


################### Caso 3 ###################

Reordering variables and trying again: