Modelo de descomposición
Una vez separados los componentes que conforman una serie de tiempo, es necesario analizar la forma en que se relacionan estos con la serie original, puesto que al recombinar los componentes es posible obtener una serie de tiempo completamente pronosticable.
Existen diferentes modelos matemáticos para expresar la serie original
$Y_t$, en términos de los componentes de tendencia $T_t$,
estacionalidad $S_t$, fluctuaciones cíclicas $C_t$ y errores
$\varepsilon_t$, en donde, es posible ajustar la serie original a uno
solo uno de los cuatro componentes o es una combinación de todos ellos,
para la posterior realización de pronósticos. Para combinar los
componentes, se tienen dos clases básicas de modelos matemáticos
- Modelo aditivo:
$Y_t = T_t + S_t + C_t + \varepsilon_t$ - Modelo multiplicativo:
$Y_t = T_t * S_t * C_t * \varepsilon_t$
en donde, como se mencionó en la subsección anterior, las fluctuaciones
cíclicas $C_t$ son el componente más difíciles de pronosticar, y por
tanto, son mezcladas con el componente de error $\varepsilon_t$ o se
asume que son parte de la tendencia $T_t$. Entonces, el modelo aditivo
y multiplicativo, pueden ser reescritos como
- Modelo aditivo:
$Y_t = T_t + S_t + \varepsilon_t$ - Modelo multiplicativo:
$Y_t = T_t * S_t * \varepsilon_t$
Es de anotar que en el modelo aditivo se supone que los tres componentes de la serie de tiempo son independientes entre sí, y es apropiado emplearlo cuando la magnitud de las fluctuaciones estacionales de la serie no varía al hacerlo la tendencia, es decir, la serie de tiempo original tiene aproximadamente la misma variabilidad a lo largo de toda la serie.
Mientras que, en el modelo multiplicativo se trabaja bajo el supuesto de que los tres componentes de la serie de tiempo no son necesariamente independientes, y es apropiados emplearlo cuando la magnitud de las fluctuaciones estacionales de la serie crece y decrece proporcionalmente con los crecimientos y decrecimientos de la tendencia, respectivamente, es decir, los valores de la serie se dispersan conforme la tendencia aumenta, o se reúnen conforme la tendencia disminuye.
Adicionalmente, se destaca que muy a menudo las series, a pesar de no tener un comportamiento aditivo, pueden ser transformadas para ser modeladas de forma aditiva. Un ejemplo de ello son los logaritmos naturales, en donde, es posible convertir el modelo multiplicativo en un modelo aditivo, ya que si
\begin{align*} Y_t = T_t * S_t * \varepsilon_t \end{align*}
entonces
\begin{align*} log(Y_t) = log(T_t) + log(S_t) + log(\varepsilon_t) \end{align*}
y por tanto, es posible realizar los pronosticos necesarios mediante una transformación, y una vez obtenidos estos, retornar los valores a la escala multiplicativa original.
Un aspecto importante, sobre los modelos aditivos y multiplicativos es
que, en el modelo aditivo siempre se asume que
$\varepsilon_t\stackrel{iid}{\sim}N(0,\sigma^2)$, mientras que para el
modelo multiplicativo, se sume que
$\varepsilon_t\stackrel{iid}{\sim}lognormal(\mu=0,\sigma^2)$, y por
tanto, mediante la transformación logaritmica del modelo multiplicativo
se tiene que $log(\varepsilon_t)\stackrel{iid}{\sim}N(0,\sigma^2)$.
Una alternativa para evaluar si los componentes de error son o no
normales, es mediante los gráficos $QQ$-plot de la distribución
Normal, y mediante la prueba Shapiro-Wilk. Éstas pueden realizarse en
R mediante las funciones qqnorm() y shapiro.test(),
respectivamente.
Existen algunas variantes para los modelos de descomposición básicos, tales como
- Modelo mixto:
$Y_t = T_t * S_t + \varepsilon_t$ - Modelo pseudo-aditivo:
$Y_t = T_t (S_t + \varepsilon_t - 1)$
los cuales se emplean en situaciones específicas, como por ejemplo, cuando la serie original posee fluctuaciones estacionales marcadamente pronunciadas y un movimiento de ciclos de tendencia, que es extremadamente dependiente del clima, o cuando la serie original posea un mes (o trimestre) que es mucho más alto o más bajo que todos los otros meses (o trimestres), respectivamente.
Clasificación descriptiva de las series de tiempo
Dadas las diferentes características que puede tener las series de tiempo, podemos clasificar su comportamiento en
- Estacionaria: Una serie es estacionaria cuando posee una media y varianza constantes en el tiempo, y en consecuencia, se observará que tiene un comportamiento estable, centrado sobre su valor promedio, con oscilaciones alrededor de este valor constante.
- No estacionaria: Una series es no estacionaria cuando no posee una media ni una varianza constantes, y en consecuencia, se observará que su valor promedio tendrá una tendencia creciente o decreciente a largo plazo, con un comportamiento que no oscilará alrededor de un valor constante.
Identificación de componentes
Autocorrelación
Uno de los aspectos más importantes de la series de tiempo es que sus observaciones no son independientes de sus observaciones pasadas, y por ello, debe realizarse un análisis de dependencia o correlación entre las observaciones y sus rezagos, el cual posee el nombre de análisis de autocorrelación, correlación serial o covariación.
El objetivo será entonces, usar la estructura de correlación que posee la serie temporal consigo misma, para tratar de explicar parte de su variación, identificar si existe de forma analítica patrones repetitivos que se encuentran enmascarados bajo el ruido y observar a partir de qué rezago deja de ser significativo el efecto que tienen éstos sobre las demás observaciones.
Con tal proposito en mente, en una serie de tiempo, se define la
varianza muestral de las observaciones como
\begin{align*} Var(Y_t) = \hat{\gamma}(0) = \mathbb E(y_t - \bar{y})^2 = \frac{1}{T-1}\sum_{t=1}^{T}(y_t-\bar{y})^2 \end{align*}
la autocovarianza muestral entre observaciones que se encuentran a $k$
periodos de tiempo de diferencia, como
\begin{align*} Cov(Y_t,Y_{t+k}) = \hat{\gamma}(k) = \mathbb E[(y_{t+k} - \bar{y})(y_{t} - \bar{y})] = \frac{1}{T-1}\sum_{t=1}^{T-k}(y_{t+k} - \bar{y})(y_{t} - \bar{y}) \end{align*}
y la autocorrelación muestral entre observaciones que se encuentran a
$k$ periodos de tiempo de diferencia, como
\begin{align*} Cor(Y_t,Y_{t+k}) = \hat{\rho(k)} = \frac{\hat{\gamma}(k)}{\hat{\gamma}(0)} = \frac{\sum_{t=1}^{T-k}(y_{t+k} - \bar{y})(y_{t} - \bar{y})}{\sum_{t=1}^{T}(y_t-\bar{y})^2} \end{align*}
donde $k$ es el número de rezagos o autocorrelaciones que se desean
calcular. Por tanto, no se recomienda emplear valores de $k$ muy
altos, ya que ésto provocará que se tengan menos términos para el
cálculo de las autocorrelaciones.
La selección del número de autocorrelaciónes puede llevarse a cabo
arbitrariamente a partir de los conocimientos del investigador, o
mediante la regla empírica para el número máximo de rezagos que deben
seleccionarse $max(k)=\left\lceil\frac{T}{4}\right\rceil$.
Para facilitar la visualización e interpretación de la autocorrelación,
se emplea un gráfico conocido como correlograma o función de
autocorrelación (ACF), la cual muestran la correlación que hay entre
observaciones separadas por $k$ intervalos de tiempo o “lags”.
A continuación se presenta el correlograma del total mensual de pasajeros de líneas aéreas internacionales, para los años 1949 a 1960
data(AirPassengers) # Carga base de datos de AirPassengers
AP <- AirPassengers # Guarda base de datos de AirPassengers
acf(AP, main = "Número de Pasajeros Aéreos")
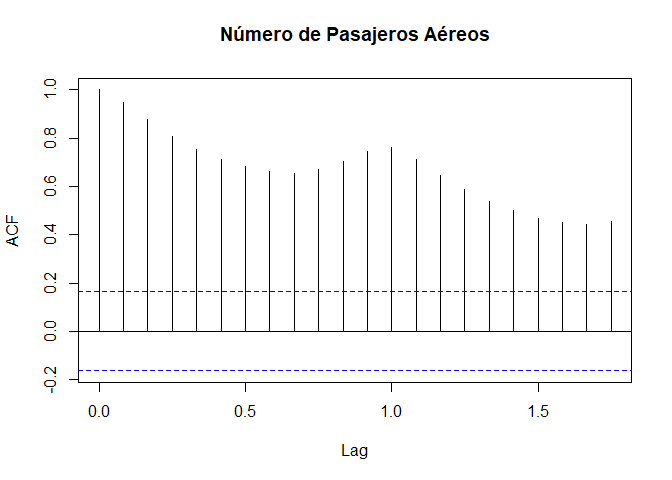
Para el caso de las variaciones porcentual de los ingresos reales totales de hoteles en Colombia entre Junio 2005 y Marzo 2019 se tiene que
library(readxl) ## Cargar librería
datos <- read_xlsx("../../Dataset/ingresorealhoteles2019.xlsx") # Cargar el archivo
ingH <- ts(datos$`Variacion ingresos`, start = c(2005, 7), frequency = 12) #
acf(ingH, main = "ACF para variaciones porcentual ingresos reales totales de hoteles")
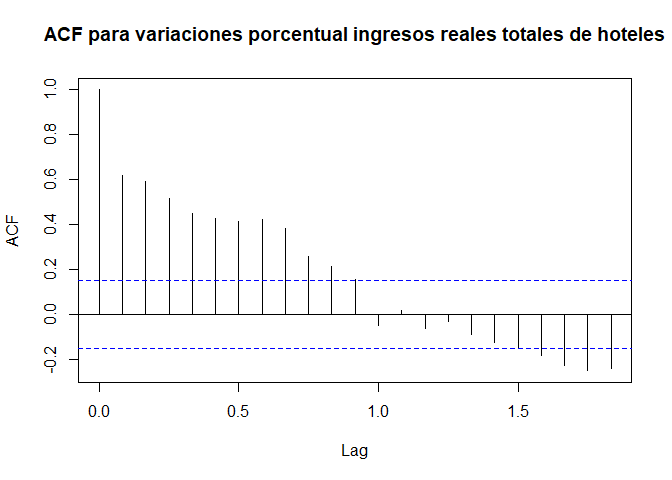
Interpretación correlograma e identificación de componentes
Basados en Rios and Hurtado (2008), los criterios para la interpretación del correlograma están dados por
- La altura de la líneas en el correlograma representa la correlación entre las observaciones que están separadas por la cantidad de unidades de tiempo que aparecen en el eje horizontal.
- La correlación para el primer rezago siempre es uno por lo que no deben tomarse en cuenta en las interpretaciones.
- Una autocorrelación es significativa si ésta se encuentra por encima o por debajo de las bandas de confianza (región crítica), la cual se construye con un nivel de confianza del 95% y asumiendo normalidad, mediante la formula:
\begin{align*} \pm Z_{\frac{\alpha}{2}}/\sqrt{T} = \pm 1.96/\sqrt{T} \end{align*}
- Si las autocorrelaciones decrecen lentamente a cero, o muestra un patrón cíclico, pasando por cero varias veces, la serie no es estacionaria. Se tendrá que diferenciarla una o más veces antes de modelarla.
- Si las autocorrelaciones muestran estacionalidad, o se tiene una alza cada periodo (cada 12 meses, por ejemplo), la serie no es estacionaria y hay que diferenciarla con un salto igual al periodo.
- Si las autocorrelaciones decrece rapidamente a cero con al menos un rezago significativo, se tendrá que la serie es estacionaria en media.
- Si ninguna de las autocorrelaciones es significativamente diferente de cero, la serie es esencialmente ruido blanco.
set.seed(1613)
par(mfrow = c(1, 2)) # Función para poner más de un gráfico
ruido <- rnorm(100, mean = 0, sd = 1)
plot.ts(ruido, type = "l", main = "Ejemplo Ruido Blanco", ylab = "Serie")
acf(ruido, main = "Ejemplo ACF Ruido Blanco")
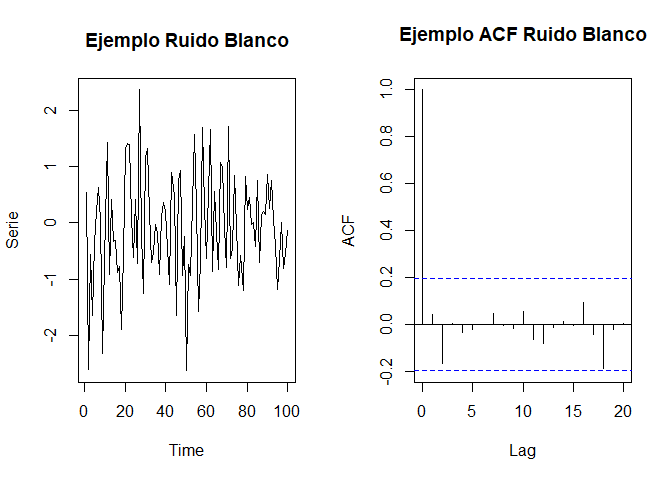
A continuación se presenta el correlograma de la diferenciación de un salto igual a 12 meses del total mensual de pasajeros de líneas aéreas internacionales, para los años 1949 a 1960.
AP12 <- diff(AP, lag = 12)
acf(AP12, main = "ACF diff(total de pasajeros de líneas aéreas, 12)")
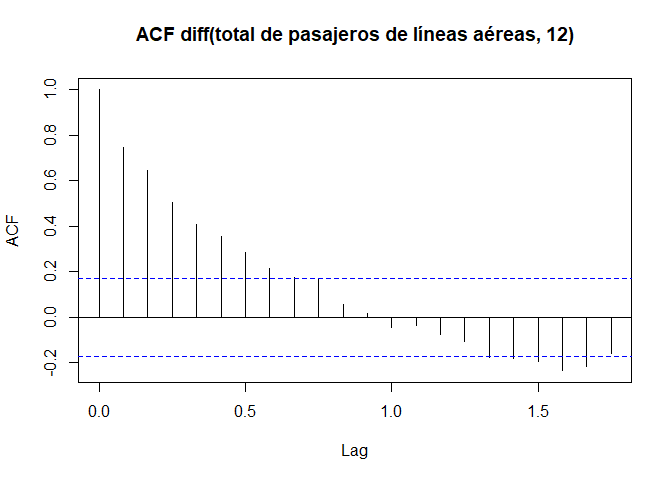
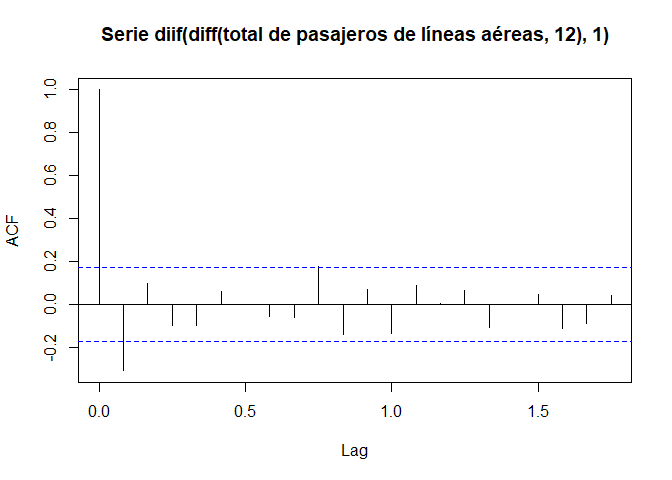
Posteriormente se presenta el correlograma de la doble diferenciación 1 mes y de un salto igual a 12 meses para el total mensual de pasajeros de líneas aéreas internacionales, para los años 1949 a 1960.
AP121 <- diff(AP12, lag = 1)
acf(AP121, main = "Serie diif(diff(total de pasajeros de líneas aéreas, 12), 1)")
Bibliografía
Rios, G., and Hurtado, C. (2008). Series de tiempo. Universidad De Chile.