Introducción
Una serie de tiempo es una secuencia de observaciones registradas y
ordenadas de forma periódica, en intervalos de tiempo igualmente
espaciados, tales como, días, meses, semestres, años, entre otros. Estas
observaciones son caracterizadas por una variable aleatoria $Y_t$, la
cual depende del tiempo $t=1,2,\ldots,T$, y donde el objetivo es
modelar el comportamiento de $Y_t$ contra $t$, siendo $T$ el
número total de observaciones que se tenga en la serie de tiempo.
Un ejemplo de una serie temporal, se presenta a continuación donde se
muestra el % anual del $PIB$ per cápita de Colombia, para un intervalo
de tiempo anual que va desde 1961 hasta 2017
Otro ejemplo, se presenta para el material particulado $PM_{10}$ y
$PM_{2.5}$ en la ciudad de Medellín para el mes de abril del año 2019,
para el cual se realizan los registros en intervalos de una hora
Es de anotar que, para el estudio de series de tiempo, se requiere de procedimientos estadísticos diferentes a los análisis empleados tradicionalmente, debido a la dependencia o correlación existente entre los diferentes puntos observados en el tiempo, la cual no permite suponer que el conjunto de datos sea independiente e idénticamente distribuido, y en consecuencia, se hace necesario el empleo de modelos estadísticos que permitan explicar el comportamiento de variables aleatorias que dependan del tiempo, para así poder realizar inferencia sobre éstas.
Entre los principales objetivos del análisis de series de tiempo, se destaca el comprender, describir e identificar patrones en el comportamiento de las series, evidenciar el efecto de acciones o decisiones pasadas (intervenciones), realizar pronósticos que contribuyan al proceso de toma de decisiones, entre otros.
Pronósticos
Un pronóstico es una predicción de algún evento futuros, que se hace a partir de los datos pasados que se conocen sobre el suceso específico. Generalmente, los pronósticos son empleados en la toma de decisiones, pues permiten disminuir la incertidumbre sobre el futuro, facilitan los procesos de planificación y control.
Métodos de pronóstico
Un factor importante en la realización de pronósticos, es el método de pronóstico que se va a emplear. Según lo planteado por Chase, Jacobs, and Aquilano (2009, pp. 469–470), los pronósticos pueden ser clasificados en cuatro tipos diferentes, los cuales se definen como técnicas cualitativas, análisis de series de tiempo, relaciones causales o econométricas y modelos de simulación.
Técnicas cualitativas
Los pronósticos cualitativos son basados en opiniones subjetivas, en donde, la información empleada para realizar el pronóstico, se obtiene mediante el juicio de un grupo de expertos en el tema, con amplia experiencia en el área de interés, el cual entrega valores o rangos de valores sobre el comportamiento futuro de la variable de estudio. Usualmente este método se emplea cuando la información que se tiene de la variable de interés, es escasa, no puede ser cuantificada o es poco confiable.
Entre las técnicas empleadas para realizar pronósticos subjetivos se destacan
- Técnicas acumulativas
- Investigación de mercados
- Grupos de consenso
- Analogía histórica
- Método Delphi
Análisis de series de tiempo
Los pronósticos basados en análisis de series de tiempo, son aquellos que emplean la información histórica de una variable de interés, con el objetivo de descubrir patrones que permitan extrapolar dicha información, para realizar proyecciones hacia el futuro.
Entre las técnicas empleadas para realizar pronósticos mediante análisis de series de tiempo se destacan
- Promedio móvil simple
- Promedio móvil ponderado
- Suavización exponencial
- Análisis de regresión
- Técnica Box Jenkins
- Proyecciones de tendencias
Relaciones causales
Los pronósticos causales, son basados en el hecho de que la serie de tiempo de interés, posee una relación de causa-efecto con una o más variables independientes, que permiten proyectar el comportamiento de la serie de tiempo de interés dado el comportamiento que tengan las variables independientes.
Entre las técnicas empleadas para realizar pronósticos mediante análisis de series de tiempo se destacan
- Análisis de regresión
- Modelos econométricos
- Modelos de entrada/salida
- Principales indicadores
Modelos de simulación
Los pronósticos basados en modelos de simulación, son aquellos que dependen de un gran número de variables y las relaciones que poseen con factores exógenos, y por tanto, es posible hacer énfasis en la estructura del modelo, mediante la suposición del comportamiento de las variables internas y el ambiente externo para observar cómo afectan éstas a los pronósticos.
Tipos de pronóstico
Una vez definido el método de pronóstico que se desea emplear, es necesario decidir el tipo de pronóstico que se va a realizar, es decir, definir si se desea realizar un pronóstico puntual, por intervalo o de densidad.
Clases de pronóstico
También es necesario definir la clase u horizonte de tiempo para el cual se desea realizar el pronostico. Montgomery, Jennings, and Kulahci (2015, p. 2) señalan que los pronósticos puede ser clasificados en tres horizontes de tiempo
- Corto plazo: son aquellos que buscan predecir eventos futuros en un horizonte de tiempo pequeño, es decir, días, semanas o meses, y son empleados generalmente para diseñar estrategias o tomar decisiones inmediata.
- Mediano plazo: son predicciones que se realizan en un horizonte de tiempo un poco más amplio, el cual abarca estimaciones entre 1 y 2 años en el futuro, y se utiliza en general para diseñar presupuestos o procesos de producción y planeación de variables operativas.
- Largo plazo: son aquellos pronósticos que se extienden a horizontes de tiempo mucho más grandes, puesto que éstos pueden extenderse a muchos años en el futuro, y se emplean en procesos de planificación, programación y proyección de proyectos.
Monitoreo de los pronósticos
Los pronósticos, al igual que otros procesos, requieren de supervisión continua, puesto que, de no supervisar o evaluar su calidad constantemente, éste podría salirse de control y dar resultados erróneos o poco confiable.
Debido a ésto, en Hanke and Wichern (2010) se establece un diagrama de flujo, en el cual se presenta los pasos operativos para el monitoreo del proceso de pronóstico
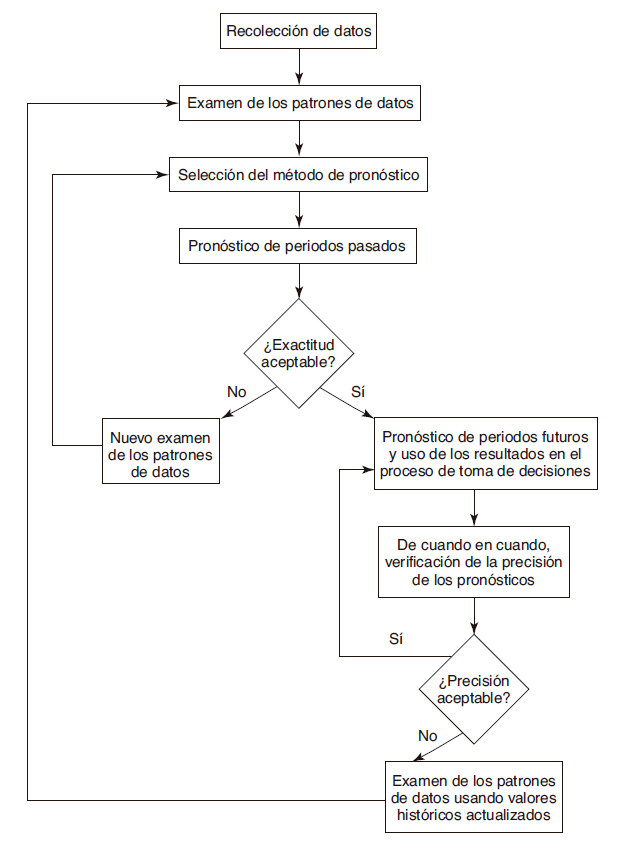
Componentes de una serie de tiempo
Para el análisis de series de tiempo, y pronostico de las mismas, es necesario realizar una adecuada selección del modelo que se va a emplear, y por ello, es fundamental hacer una precisa identificación de los componentes que conforman la serie, cuya actuación conjunta da como resultado el comportamiendo de la serie original. Estos componentes pueden ser ser divididos en cuatro, a saber, tendencia, estacionalidad, error y fluctuación cíclica.
Para ilustrar el proceso de descomposición, se emplean dos conjuntos de datos. El primer conjuto de datos, se encuentra integrado en la base de R y corresponde al total mensual de pasajeros de líneas aéreas internacionales, para los años 1949 a 1960.
data(AirPassengers) # Carga base de datos de AirPassengers
AP <- AirPassengers # Guarda base de datos de AirPassengers
descAP <- stl(AP, s.window = 12)
plot(descAP, main = "Componentes del total de pasajeros de líneas aéreas", col = "chocolate1",
lwd = 2)
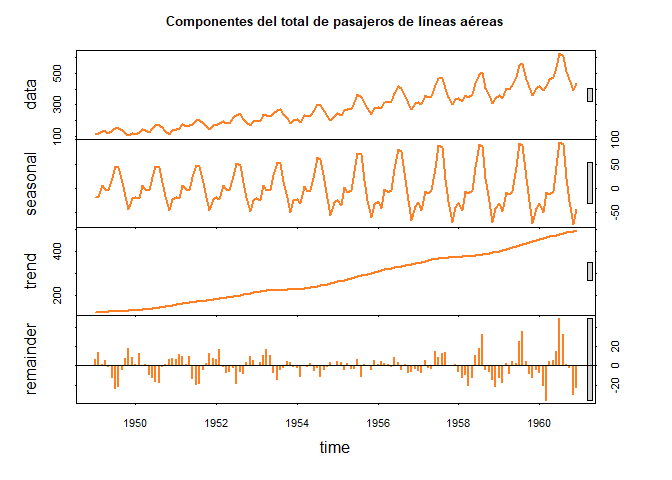
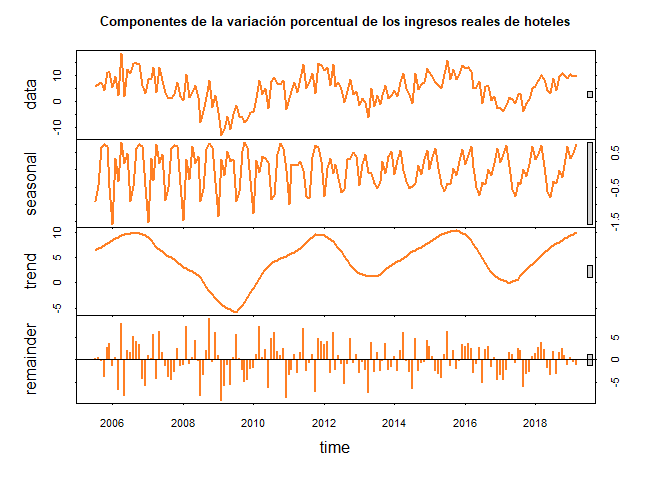
El segundo conjunto de datos, corresponde a las variaciones porcentual de los ingresos reales totales de hoteles en Colombia entre Junio 2005 y Marzo 2019 Descargar.
### Instalar y cargar librerías install.packages(c('readxl', 'XLConnect'),
### dependencies = T) # Instala librerías
library(readxl) # Carga librería
library(XLConnect) # Para descargar archivos online de forma temporal
### Crea archivo temporal para cargar archivo online
temp <- tempfile(fileext = ".xlsx")
dataURL <- "https://github.com/jiperezga/jiperezga.github.io/raw/master/Dataset/ingresorealhoteles2019.xlsx"
download.file(dataURL, destfile = temp, mode = "wb")
datos <- read_xlsx(temp) # Cargar el archivo
# datos <- read_xlsx(file.choose()) # para buscar archivo guardado en el PC
ingH <- ts(datos$`Variacion ingresos`, start = c(2005, 7), frequency = 12) # Transforma observaciones a tipo time-series
descIH <- stl(ingH, s.window = 12)
plot(descIH, main = "Componentes de la variación porcentual de los ingresos reales de hoteles",
col = "chocolate1", lwd = 2)
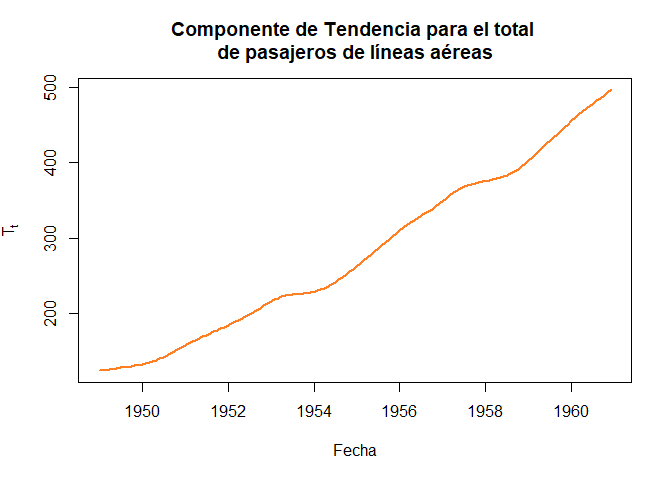
Componente de tendencia
El componente de tendencia se denota por $T_t$, es el componente de la
serie que cambia más lentamente y describe el patrón suave que tiene una
serie a largo plazo respecto a su nivel promedio (evolución a largo
plazo de su media), el cual es caracterizado por un crecimiento o
decrecimiento presistente. El comportamiento de la tendencia, puede ser
explicado por el crecimiento o cambio de la población, el cambio
tecnológico, el crecimiento económico, etc.
Para el caso del total mensual de pasajeros de líneas aéreas internacionales, para los años 1949 a 1960 se tiene que
fechasAP <- seq(as.Date("1949/1/1"), length.out = length(AP), by = "month") ## Se definen fechas
plot(x = fechasAP, y = descAP$time.series[, 2], main = "Componente de Tendencia para el total
de pasajeros de líneas aéreas",
xlab = "Fecha", ylab = expression(T[t]), col = "chocolate1", type = "l",
pch = 19, lwd = 2)
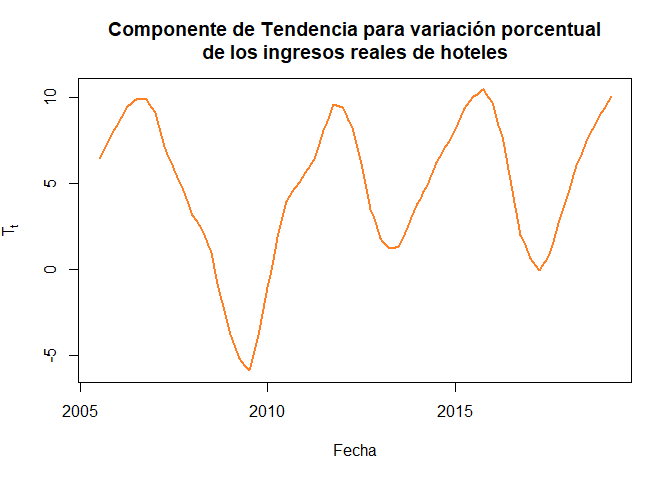
Mientras que, para el caso de las variaciones porcentual de los ingresos reales totales de hoteles en Colombia entre Junio 2005 y Marzo 2019 se tiene que
fechasIH <- seq(as.Date("2005/7/1"), length.out = length(ingH), by = "month") ## Se definen fechas
plot(x = fechasIH, y = descIH$time.series[, 2], main = "Componente de Tendencia para variación porcentual
de los ingresos reales de hoteles",
xlab = "Fecha", ylab = expression(T[t]), col = "chocolate1", type = "l",
pch = 19, lwd = 2)
Componente estacional
El componente estacional se denota como $S_t$, es el segundo
componente de la serie que cambia más rápidamente y se describe como un
patrón que se repite regularmente a través de la serie sobre una base
anual. Este comportamiento es debido a factores tales como los consumos
o las estaciones climáticas, es decir factores que ocurren con una
periodicidad semanal, mensual, trimestral, o semestral.
Es de anotar, que los efectos estacionales son fáciles de entender y se pueden medir explícitamente o incluso se pueden eliminar de la serie de datos, el cual es llamado desestacionalización de la serie.
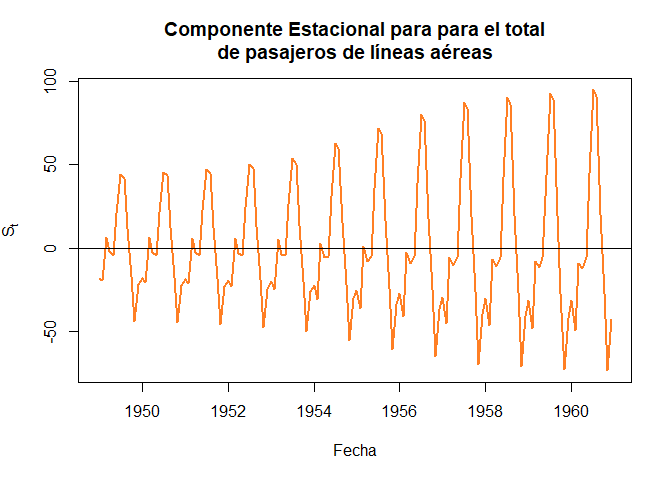
Para el caso del total mensual de pasajeros de líneas aéreas internacionales, para los años 1949 a 1960 se tiene que
plot(x = fechasAP, y = descAP$time.series[, 1], main = "Componente Estacional para para el total
de pasajeros de líneas aéreas",
xlab = "Fecha", ylab = expression(S[t]), col = "chocolate1", type = "l",
pch = 19, lwd = 2)
abline(h = 0)
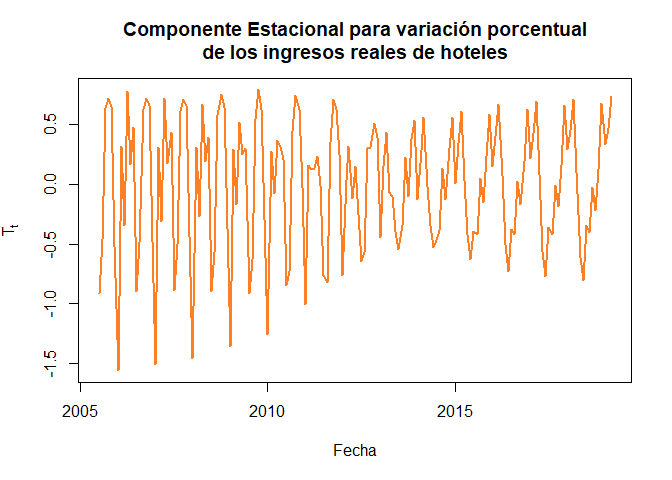
Mientras que, para el caso de las variaciones porcentual de los ingresos reales totales de hoteles en Colombia entre Junio 2005 y Marzo 2019 se tiene que
plot(x = fechasIH, y = descIH$time.series[, 1], main = "Componente Estacional para variación porcentual
de los ingresos reales de hoteles",
xlab = "Fecha", ylab = expression(T[t]), col = "chocolate1", type = "l",
pch = 19, lwd = 2)
Componente aleatorio, irregular o de error
El componente de error se denota como $\varepsilon_t$, también llamado
ruido blanco, es el componente de la serie que cambia más
rápidamente y se caracteriza por presentar pequeñas fluctuaciones sobre
alrededor de una media y varianza constantes sin ningún patrón aparente.
Este fluctuaciones se deben generalmente, a eventos externos
impredesibles que sólo ocurre fortuitamente e inciden de forma aislada
en un instante del tiempo.
Es de anotar, que este componente es impredecible, pero puede ser
modelado como observaciones aleatorias de alguna distribución, tal como
lo es, una distribución $N(0,\sigma^2)$.
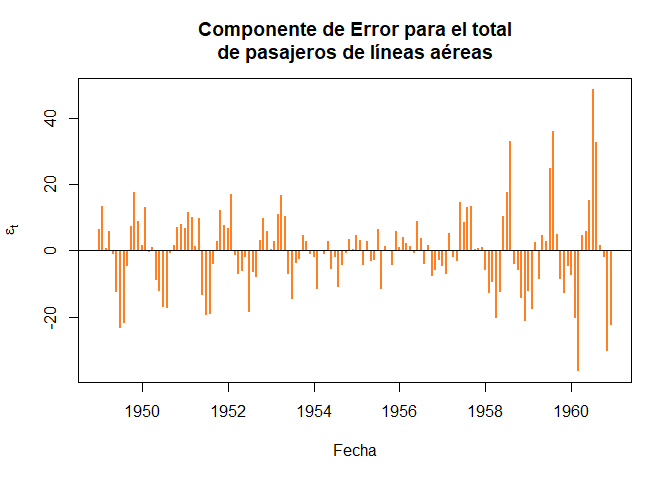
Para el caso del total mensual de pasajeros de líneas aéreas internacionales, para los años 1949 a 1960 se tiene que
plot(x = fechasAP, y = descAP$time.series[, 3], main = "Componente de Error para el total
de pasajeros de líneas aéreas",
xlab = "Fecha", ylab = expression(epsilon[t]), col = "chocolate1", type = "h",
pch = 19, lwd = 2)
abline(h = 0)
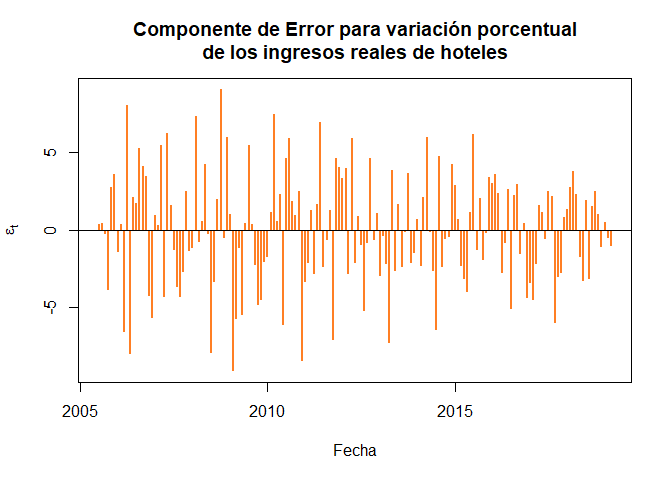
Mientras que, para el caso de las variaciones porcentual de los ingresos reales totales de hoteles en Colombia entre Junio 2005 y Marzo 2019 se tiene que
plot(x = fechasIH, y = descIH$time.series[, 3], main = "Componente de Error para variación porcentual
de los ingresos reales de hoteles",
xlab = "Fecha", ylab = expression(epsilon[t]), col = "chocolate1", type = "h",
pch = 19, lwd = 2)
abline(h = 0)
Componente de fluctuación cíclica
El componente de fluctuación cícluca se denota como $C_t$, es el
segundo componente de la serie que cambia más lentamente y se
caracteriza por presentar patrones de onda en puntos recurrentes en el
tiempo con duración más de un año. Este comportamiento es debido por
ejemplo a ciclos comerciales que dependen de prosperidad, depresión,
recesión y recuperación.
Es de anotar que, los ciclos son el componente más difíciles de
pronosticar, debido a que éstos poseen periodos más largos (medida en
años) y amplitudes irregulares (diferencias entre altas y bajas) que
están lejos de ser constantes, lo cual hace que éstos no sean fijos ni
predecibles, y por tanto, las fluctuaciones cíclicas son mezcladas
generalmente con el componente de error $\varepsilon$ o se asume que
cualquier cíclo es parte de la tendencia $T_t$.
Para el caso de las variaciones porcentual de los ingresos reales totales de hoteles en Colombia entre Junio 2005 y Marzo 2019 se tiene que
Otras componentes
Es de anotar, que además de tener tendencia, estacionalidad, error y fluctuación cíclica, algunas series de tiempo pueden presentar patrones de impulso, rampa o paso
- Patrón de impulso: Se observa cuando para uno o dos periodos, el proceso presenta un nivel superior o inferior al comportamiento original de la serie.
- Patrón de rampa: Se observa cuando aparece un cambio de tendencia repentino en el comportamiento constante de la serie, o viceversa.
- Patrón de paso: Se observa cuando hay cambio permanente en el nivel de la serie.
Bibliografía
Chase, R., Jacobs, F., and Aquilano, N. (2009). Administración de operaciones, producción y cadena de suministros . (12th ed.). McGraw-Hill Interamericana.
Hanke, J., and Wichern, D. (2010). Pronósticos en los negocios (9th ed.). Pearson educación.
Montgomery, D., Jennings, C., and Kulahci, M. (2015). Introduction to time series analysis and forecasting (2nd ed.). John Wiley & Sons.