
Intervalos de confianza
Un intervalo de confianza es un rango de valores, construidos a partir de los estadísticos muestrales, que tienen por objetivo, incluir con un nivel de confianza preestablecido, el valor real de un parámetro desconocido de una población.
Nota
- Usualmente se usan valores de de \(0.1, 0.05\) y $ 0.01$, es decir, niveles de confianza de \(0.9, 0.95\) y \(0.99\).
- La longitud o amplitud del intervalo construido, medirá la precisión de la estimación realizada, por tanto, intervalos largos proporcionan estimaciones más imprecisas, mientras que intervalos cortos proporcionan estimaciones más precisas.
- A medida que aumenta el nivel de confianza, la amplitud del intervalo se hace más grande.
- A medida que aumenta el tamaño de muestra, la amplitud del intervalo se hace más pequeño.
Intervalos de confianza para una media $\mu$
Sea $X_1, X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$ con media $\mu$ desconocida, y varianza $\sigma^2<\infty$,
entonces dependiendo de las condiciones, se tendrán los siguientes
intervalos de confianza para la media $\mu$.
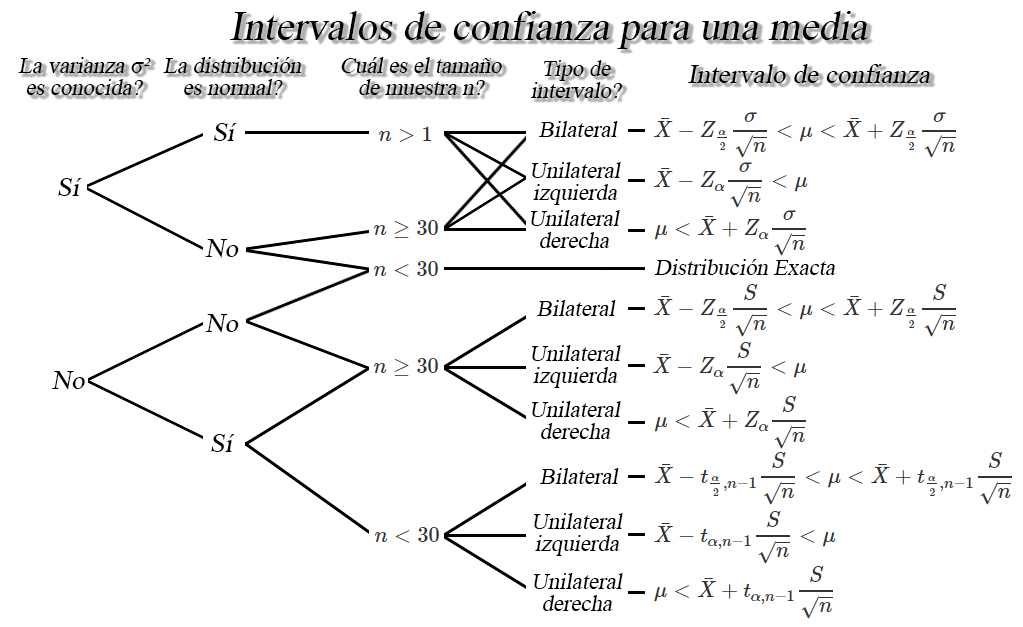
Intervalo de confianza para una media
Suponga que se desea crear un intervalo de confianza del \(90\%\) para el número promedio de pisos de la construcción (nro\(\_\)pisos). En este caso, podemos calcular un intervalo de confianza para una media en R mediante la función t.test de la forma.
# Calcula intervalo de confianza para una media R
t.test(x = datos$nro_pisos, conf.level = 0.9)
One Sample t-test
data: datos$nro_pisos
t = 267.18, df = 86146, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
90 percent confidence interval:
3.303944 3.344877
sample estimates:
mean of x
3.324411
Intervalos de confianza para diferencia de medias $\mu_1 - \mu_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias iid de
tamaños $n_1$, y $n_2$ con medias $\mu_1$ y $\mu_2$
desconocidas, y varianzas $\sigma_1^2<\infty$ y $\sigma^2_2<\infty$,
respectivamente, entonces dependiendo de las condiciones, se tendrán los
siguientes intervalos de confianza para la diferencia de medias
$\mu_1 - \mu_2$.

Intervalo de confianza para diferencia de medias
Suponga que se desea crear un intervalo de confianza del \(95\%\) para la diferencia promedio entre el precio de venta por \(m^2\) (preciovtax), en los estratos \(2\) y \(4\) (estrato). En este caso, podemos calcular un intervalo de confianza para la diferencia de media en R mediante la función t.test de la forma.
# Calcula intervalo de confianza para diferencia de medias R
t.test(x = datos$preciovtax[datos$estrato == 2], y = datos$preciovtax[datos$estrato ==
4], conf.level = 0.95, var.equal = F)
Welch Two Sample t-test
data: datos$preciovtax[datos$estrato == 2] and datos$preciovtax[datos$estrato == 4]
t = -131.04, df = 14252, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1254.805 -1217.818
sample estimates:
mean of x mean of y
938.2444 2174.5557
Intervalos de confianza para una proporción $p$
Sea $X_1,X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$, tal que $X\sim b(n,p)$ entonces si $n$ es suficientemente
grande tal que $n\geq30$, y la proporción desconocida $p$ no se
encuentre cercana a $0$ o $1$, tal que $np>5$ y $n(1-p)>5$,
entonces un intervalo de confianza para la proporción $p$ es de la
forma 
Intervalo de confianza para una proporción
Suponga que se desea crear un intervalo de confianza del \(90\%\) para la proporción de empresas que poseen licencia de construcción (ob\(\_\)formal). En este caso, podemos calcular un intervalo de confianza para una proporción en R mediante la función prop.test de la forma.
# Calcula intervalo de confianza para una proporción R
exitos <- table(datos$ob_formal)[1]
total <- sum(table(datos$ob_formal))
prop.test(x = exitos, n = total, conf.level = 0.9)
1-sample proportions test with continuity correction
data: exitos out of total, null probability 0.5
X-squared = 9080.5, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is not equal to 0.5
90 percent confidence interval:
0.3350122 0.3403242
sample estimates:
p
0.3376631
Intervalos de confianza para diferencia de proporciones $p_1 - p_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias iid de
tamaños $n_1$, y $n_2$ tal que $X_1\sim b(n,p)$ y
$X_2\sim b(n,p)$. Entonces si, $n_1$, y $n_2$ son suficientemente
grandes tal que $n_1, n_2 \geq 30$, y las proporciones desconocidas
$p_1$ y $p_2$ no se encuentran cercanas a $0$ o $1$, tal que
$n_1p_1, n_2p_2, n_1(1-p_1)$ y $n_2(1-p_2)>5$, entonces un intervalo
de confianza para la diferencia de proporciones $p_1 - p_2$ es de la
forma

Intervalo de confianza para diferencia de proporciones
Suponga que se desea crear un intervalo de confianza del \(90\%\) para la diferencia entre la proporción de empresas que poseen licencia de construcción (ob\(\_\)formal), respecto a las regiones de Bogotá y Antioquia (region). En este caso, podemos calcular un intervalo de confianza para la diferencia entre proporción en R mediante la función prop.test() de la forma.
# Calcula intervalo de confianza para diferencia de proporciones R
exitos1 <- table(datos$ob_formal[datos$region == "Bogotá"])[1]
total1 <- sum(table(datos$ob_formal[datos$region == "Bogotá"]))
exitos2 <- table(datos$ob_formal[datos$region == "Antioquia"])[1]
total2 <- sum(table(datos$ob_formal[datos$region == "Antioquia"]))
prop.test(x = c(exitos1, exitos2), n = c(total1, total2), conf.level = 0.9)
2-sample test for equality of proportions with continuity correction
data: c(exitos1, exitos2) out of c(total1, total2)
X-squared = 52.232, df = 1, p-value = 0.0000000000004933
alternative hypothesis: two.sided
90 percent confidence interval:
-0.05258971 -0.03289650
sample estimates:
prop 1 prop 2
0.4006542 0.4433973
Intervalos de confianza para una varianza $\sigma^2$
Sea $X_{1}, X_{2}, \ldots, X_{n}$ una muestra aleatoria normal de
tamaño $n$ con media $\mathbb{E}(X)=\mu$ y varianza desconocida
$Var(X)=\sigma^2<\infty$, respectivamente, entonces un intervalo de
confianza del $100(1-\alpha)\%$ para una varianza $\sigma^2$ estará
dado por

Intervalo de confianza para una varianza
Suponga que se tiene interés en encontrar un intervalo de confianza del \(95\%\), para la varianza del precio unitario de ventas por metro cuadrado (preciovtax). En este caso, podemos calcular el intervalo de confianza de interés mediante la función varTest de la librería EnvStats, mediante la estructura.
library(EnvStats)
# Calcula intervalo de confianza para una de varianza
varTest(datos$preciovtax, alternative = "two.sided", conf.level = 0.95)
Chi-Squared Test on Variance
data: datos$preciovtax
Chi-Squared = 106655714921, df = 86147, p-value < 2.2e-16
alternative hypothesis: true variance is not equal to 1
95 percent confidence interval:
1226457 1249842
sample estimates:
variance
1238067
Intervalos de confianza para razón de varianzas $\sigma^2_1/\sigma^2_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias normales
de tamaños $n_1$, y $n_2$ con medias $\mu_1$ y $\mu_2$, y
varianzas desconocidas $\sigma_1^2<\infty$ y $\sigma^2_2<\infty$,
respectivamente, entonces un intervalo de confianza del
$100(1-\alpha)\%$ para $\sigma^2_1/\sigma^2_2$ estará dada por

Intervalo de confianza para cociente de varianzas
Suponga que se desea crear un intervalo de confianza del \(95\%\) para el cociente de varianzas entre el precio de venta por \(m^2\) (preciovtax), en los estratos \(1\) y \(5\) (estrato). En este caso, podemos calcular un intervalo de confianza para el cociente de varianzas en R mediante la función var.test() de la forma.
# Calcula intervalo de confianza para cociente de varianzas R
var.test(x = datos$preciovtax[datos$estrato == 1], y = datos$preciovtax[datos$estrato ==
5], conf.level = 0.95)
F test to compare two variances
data: datos$preciovtax[datos$estrato == 1] and datos$preciovtax[datos$estrato == 5]
F = 0.034198, num df = 11170, denom df = 5010, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.03261627 0.03584061
sample estimates:
ratio of variances
0.03419778