
Medidas estadísticas
Las medidas estadísticas tienen por objetivo resumir la información contenida en un conjunto de datos, en pocos valores numéricos que representan diferentes características. Estas medidas estadísticas nos darán información sobre la situación, dispersión, forma, asociación que posee un conjunto de datos de manera que sea posible captar rápidamente la estructura de los mismos.
Medidas de tendencia central
Estas medidas tienen por objetivo buscar valores que muestren el lugar
en el cual se encuentra el centro de un conjunto de observaciones. Si se
define $x_1, x_2, \ldots, x_n$ como un conjunto de $n$
observaciones, entonces
Media
Es el promedio numérico de las $n$ observaciones.
\begin{align*} \bar{X}=\sum_{i=1}^n\frac{x_i}{n}=\frac{x_1+x_2+\ldots+x_n}{n} \end{align*}
En R, puede calcularse el valor promedio de un conjunto de
observaciones mediante la función mean(datos).
Ejercicio Caso de Estudio
Calcule el precio promedio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del precio promedio de venta en
metros cuadrados, se emplea la función mean() tal que
mean(datos$preciovtax)
[1] 1524.358
Lo cual significa que en promedio el precio de venta en metros cuadrados, sin incluir el garaje, en miles de pesos es de \(1524.358\).
Mediana
Es el valor que ocupa el lugar central en un conjunto de datos, es
decir, el valor que divide el conjunto de observaciones en dos partes
que contienen el 50% de las observaciones. Para realizar el cálculo de
la mediana es necesario ordenar inicialmente el conjunto de
observaciones de forma ascendente.
\begin{align*} \tilde{X}=\begin{cases}x_{\left[\frac{(n+1)}{2}\right]} & \text{si } n \text{ es impar}\\\frac{1}{2}\left(x_{\left[\frac{n}{2}\right]}+x_{\left[\frac{n}{2}+1\right]}\right) & \text{si } n \text{ es par}\end{cases} \end{align*}
donde $x_{\left[j\right]}$ representa la $j$-ésima observación
ordenada. En R puede calcularse la mediana de un conjunto de
observaciones mediante la función median(datos).
Ejercicio Caso de Estudio
Calcule el precio mediano de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del precio mediano de venta en
metros cuadrados en miles de pesos, sin incluir el garaje del bien, se
emplea la función median() tal que
median(datos$preciovtax)
[1] 1200
Lo cual significa que el precio mediano de venta en metros cuadrados, en miles de pesos sin incluir el garaje es de \(1200\).
Moda
Es el valor que ocurre con mayor frecuencia en un conjunto de datos, es decir, es la observación que se repite con mayor frecuencia. Es de anotar que en un conjunto de observaciones, se puede tener más de una moda, en cuyo caso se dirá que el conjunto de datos es bimodal, trimodal o multimodal.
Entre las funciones base del programa R no hay ninguna función que calcule la moda de un conjunto de observaciones, y por tanto, debe crearse una función que realice el cálculo, de la forma
# Función para el cálculo de la moda
Moda <- function(x) {
keys <- na.omit(unique(x))
keys[which.max(tabulate(match(x, keys)))]
}
Una vez creada la función, puede calcularse la moda de un conjunto de
observaciones mediante la función Moda(datos).
Ejercicio Caso de Estudio
Calcule el precio modal de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del precio modal de venta en
metros cuadrados en miles de pesos, sin incluir el garaje del bien, se
emplea la función Moda() que se creó previamente, tal que
### Se crea la función
Moda <- function(x) {
keys <- na.omit(unique(x))
keys[which.max(tabulate(match(x, keys)))]
}
### Se realiza el cálculo de la moda
Moda(datos$preciovtax)
[1] 1000
Lo cual significa que el precio de venta por en metros cuadrados que más se repite, en miles de pesos sin incluir el garaje es de \(1000\).
Media recortada
Es una medida similar a la media, con la diferencia de que, en este
caso, se ordenan las observaciones de forma ascendente, y luego se
recortan un número $r$ observaciones superiores e inferiores, tal que
$r=n\times trim$, $trim$ un valor porcentual entre 0 y 0.5
\begin{align*} \bar{X}_{trim}=\frac{1}{n-2r}\sum_{i={r+1}}^{n-r}x_i \end{align*}
En R, puede calcularse el valor de la media recortada de un
conjunto de observaciones mediante la función
mean(datos, trim = trim).
Ejercicio Caso de Estudio
Calcule el precio promedio de venta en metros cuadrados preciovtax, recortada al \(10\%\).
Solución en R
Para realizar el cálculo en R del precio promedio de venta en
metros cuadrados recordando los datos al \(10\%\), se emplea la función
mean(), junto con el argumento trim = 0.10 tal
que
mean(datos$preciovtax, trim = 0.1)
[1] 1336
Lo cual significa que al eliminar la influencia del \(10\%\) superior e inferior de los datos, se tiene que en promedio el precio de venta en metros cuadrados, sin incluir el garaje, en miles de pesos es de \(1336\).
Medidas de localización
Estas medidas tienen por objetivo dividir un conjunto de datos ordenado
en partes iguales, entendidas estas como intervalos que contienen la
misma proporción de observaciones. Si se define
$x_{[1]}, x_{[2]}, \ldots, x_{[n]}$, como un conjunto de $n$
observaciones ordenadas en forma creciente, entonces
Cuartil
Son los tres valores $(j=1,2,3)$, que dividen a un conjunto de
datos ordenados en cuatro partes iguales. Para ello, es necesario
calcular inicialmente una variable $h_j$ de posicionamiento dado el
cuartil $j$ de interés, tal que
\begin{align*} h_j = \frac{j(n-1)}{4} + 1 \quad \quad j=1,2,3 \end{align*}
y posteriormente, con éste valor se realiza el cálculo del cuartil de
interés
\begin{align*} C_j=x_{\lfloor h_j\rfloor]} + \left((h_j - \lfloor h_j\rfloor) \times (x_{[\lfloor h_j\rfloor + 1]} - x_{\lfloor h_j\rfloor}) \right) \quad \quad j=1,2,3 \end{align*}
siendo $\lfloor h_j\rfloor$ el valor piso de $h_j$, es decir, el
entero de $h$ aproximando siempre hacia abajo.
Representación Cuartil
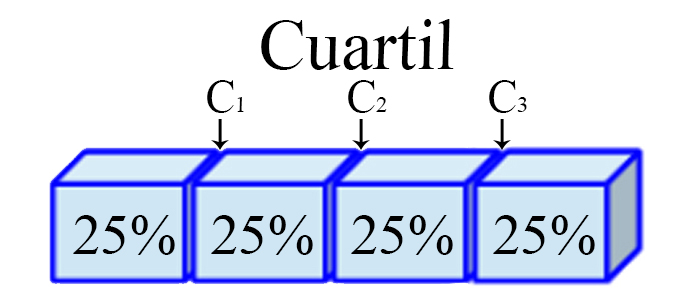
En R puede calcularse los cuartiles de un conjunto de
observaciones mediante la función
quantile(datos, probs = c(0.25, 0.5, 0.75)).
Ejercicio Caso de Estudio
Calcule el valor de los tres cuartiles asociados a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R de los tres cuartiles asociados
al precio de venta en metros cuadrados, se emplea la función
quantile(), junto con el argumento probs = c(0.25,
0.5, 0.75) tal que
quantile(datos$preciovtax, probs = c(0.25, 0.5, 0.75))
25% 50% 75%
790 1200 1900
Encontrando que los tres valores que dividen el precio de venta en metros cuadrados en cuatro partes iguales son, \(790\), \(1200\) y \(1900\).
Quintil
Son los cuatro valores $(j=1,2,3,4)$, que dividen a un conjunto de
datos ordenados en cinco partes iguales. Para ello, es necesario
calcular inicialmente una variable $h_j$ de posicionamiento dado el
quintil $j$ de interés, tal que
\begin{align*} h_j = \frac{j(n-1)}{5} + 1 \quad \quad j=1,2,3,4 \end{align*}
y posteriormente, con éste valor se realiza el cálculo del quintil de
interés
\begin{align*} Q_j=x_{\lfloor h_j\rfloor]} + \left((h_j - \lfloor h_j\rfloor) \times (x_{[\lfloor h_j\rfloor + 1]} - x_{\lfloor h_j\rfloor}) \right) \quad \quad j=1,2,3,4 \end{align*}
siendo $\lfloor h_j\rfloor$ el valor piso de $h_j$, es decir, el
entero de $h$ aproximando siempre hacia abajo.
Representación Quintil
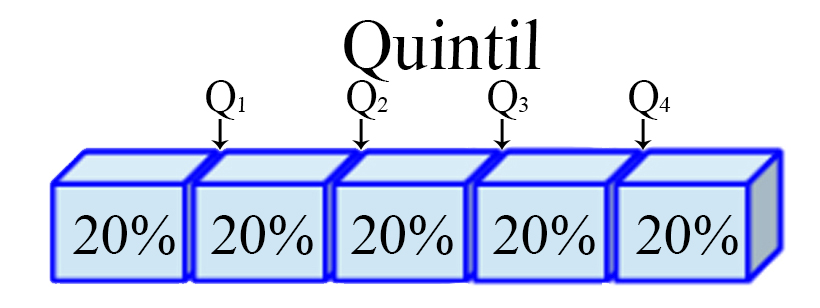
En R pueden calcularse los quintiles de un conjunto de
observaciones mediante la función
quantile(datos, probs = c(0.2, 0.4, 0.6, 0.8)).
Ejercicio Caso de Estudio
Calcule el valor de los cuatro quintiles asociados a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R de los cuatro quintiles asociados
al precio de venta en metros cuadrados, se emplea la función
quantile(), junto con el argumento probs = c(0.2,
0.4, 0.6, 0.8) tal que
quantile(datos$preciovtax, probs = c(0.2, 0.4, 0.6, 0.8))
20% 40% 60% 80%
700.0 1000.0 1433.0 2110.6
Encontrando que los cuatro valores que dividen el precio de venta en metros cuadrados en cinco partes iguales son, \(700\), \(1000\), \(1433\) y \(2110.6\).
Decil
Son los nueve valores $(j=1,2,\ldots,9)$, que dividen a un
conjunto de datos ordenados en diez partes iguales. Para ello, es
necesario calcular inicialmente una variable $h_j$ de posicionamiento
dado el decil $j$ de interés, tal que
\begin{align*} h_j = \frac{j(n-1)}{10} + 1 \quad \quad j=1,2,\dots,9 \end{align*}
y posteriormente, con éste valor se realiza el cálculo del decil de
interés
\begin{align*} D_j=x_{\lfloor h_j\rfloor]} + \left((h_j - \lfloor h_j\rfloor) \times (x_{[\lfloor h_j\rfloor + 1]} - x_{\lfloor h_j\rfloor}) \right) \quad \quad j=1,2,\dots,9 \end{align*}
siendo $\lfloor h_j\rfloor$ el valor piso de $h_j$, es decir, el
entero de $h$ aproximando siempre hacia abajo.
Representación Decil
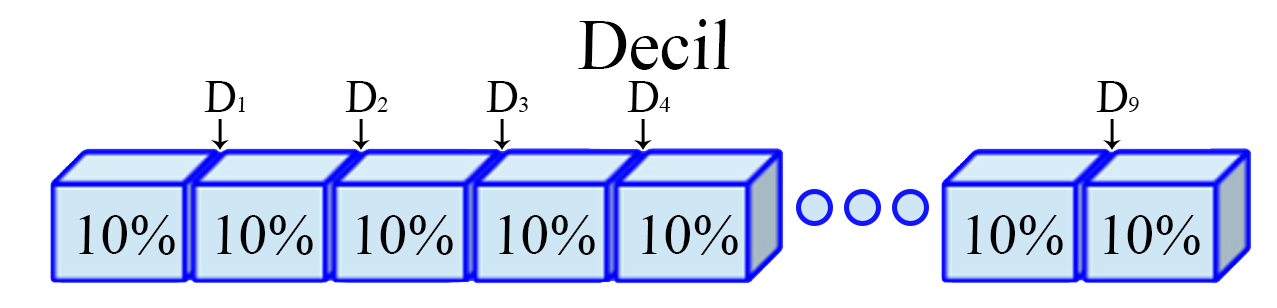
En R pueden calcularse los deciles de un conjunto de
observaciones mediante la función
quantile(datos, probs = seq(0.1, 0.9, 0.1)).
Ejercicio Caso de Estudio
Calcule el valor de los nueve deciles asociados a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R de los nueve deciles asociados al
precio de venta en metros cuadrados, se emplea la función
quantile(), junto con el argumento probs = seq(0.1,
0.9, 0.1) tal que
quantile(datos$preciovtax, probs = seq(0.1, 0.9, 0.1))
10% 20% 30% 40% 50% 60% 70% 80% 90%
580.0 700.0 850.0 1000.0 1200.0 1433.0 1748.0 2110.6 2844.0
Encontrando que los nueve valores que dividen el precio de venta en metros cuadrados en diez partes iguales son, \(580\), \(700\), \(850\), \(1000\), \(1200\), \(1433\), \(1748\), \(2110.6\), \(2844\).
Percentil
Son los noventa y nueve valores $(j=1,2,\ldots,99)$, que dividen a
un conjunto de datos ordenados en cien partes iguales. Para ello, es
necesario calcular inicialmente una variable $h_j$ de posicionamiento
dado el percentil $j$ de interés, tal que
\begin{align*} h_j = \frac{j(n-1)}{100} + 1 \quad \quad j=1,2,\dots,99 \end{align*}
y posteriormente, con éste valor se realiza el cálculo del percentil de
interés
\begin{align*} P_j=x_{\lfloor h_j\rfloor]} + \left((h_j - \lfloor h_j\rfloor) \times (x_{[\lfloor h_j\rfloor + 1]} - x_{\lfloor h_j\rfloor}) \right) \quad \quad j=1,2,\dots,99 \end{align*}
siendo $\lfloor h_j\rfloor$ el valor piso de $h_j$, es decir, el
entero de $h$ aproximando siempre hacia abajo.
Representación Percentil
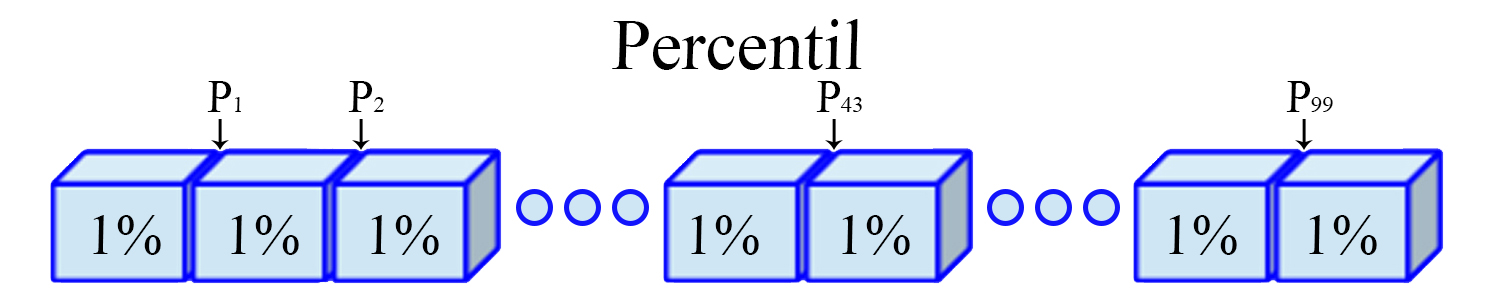
En R pueden calcularse los percentiles de un conjunto de
observaciones mediante la función
quantile(datos, probs = seq(0.01, 0.99, 0.01)).
Ejercicio Caso de Estudio
Calcule el valor de los noventa y nueve percentiles asociados a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R de los noventa y nueve
percentiles asociados al precio de venta en metros cuadrados, se emplea
la función quantile(), junto con el argumento probs =
seq(0.01, 0.99, 0.01) tal que
quantile(datos$preciovtax, probs = seq(0.01, 0.99, 0.01))
1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 11%
350.0 400.0 430.0 459.0 500.0 500.0 510.0 545.0 550.0 580.0 600.0
12% 13% 14% 15% 16% 17% 18% 19% 20% 21% 22%
600.0 600.0 630.0 650.0 650.0 680.0 700.0 700.0 700.0 714.0 740.0
23% 24% 25% 26% 27% 28% 29% 30% 31% 32% 33%
750.0 760.0 790.0 800.0 800.0 809.0 833.0 850.0 860.0 890.0 900.0
34% 35% 36% 37% 38% 39% 40% 41% 42% 43% 44%
900.0 915.0 948.0 952.0 980.0 1000.0 1000.0 1000.0 1010.0 1050.0 1073.0
45% 46% 47% 48% 49% 50% 51% 52% 53% 54% 55%
1100.0 1100.0 1111.0 1150.0 1200.0 1200.0 1200.0 1218.0 1250.0 1300.0 1300.0
56% 57% 58% 59% 60% 61% 62% 63% 64% 65% 66%
1320.0 1350.0 1397.0 1400.0 1433.0 1480.0 1500.0 1500.0 1538.0 1587.0 1600.0
67% 68% 69% 70% 71% 72% 73% 74% 75% 76% 77%
1622.0 1667.0 1700.0 1748.0 1800.0 1800.0 1820.0 1881.0 1900.0 1981.0 2000.0
78% 79% 80% 81% 82% 83% 84% 85% 86% 87% 88%
2000.0 2089.0 2110.6 2200.0 2231.0 2300.0 2390.0 2450.0 2500.0 2550.0 2637.0
89% 90% 91% 92% 93% 94% 95% 96% 97% 98% 99%
2777.0 2844.0 3000.0 3100.0 3300.0 3500.0 3707.0 4000.0 4300.0 4800.0 5800.0
Encontrando que los noventa y nueve valores que dividen el precio de venta en metros cuadrados en cien partes.
Medidas de dispersión
Estas medidas tienen por objetivo determinar la dispersión o
variabilidad que posee un conjunto de observaciones, en donde, entre
mayor sean estas medidas, mayor será el grado de dispersión de los
datos. Si se define $x_1, x_2, \ldots, x_n$ como un conjunto de $n$
observaciones, entonces
Varianza
Mide la distancia media al cuadrado del conjunto de datos respecto a
la media
\begin{align*} S^2=\frac{1}{n-1}\sum_{i=1}^n{(x_i-\bar{X})^2} \end{align*}
En R puede calcularse la varianza de un conjunto de
observaciones mediante la función var(datos).
Ejercicio Caso de Estudio
Calcule el valor de la varianza asociada a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R de la varianza asociada al precio
de venta en metros cuadrados, se emplea la función var(),
tal que
var(datos$preciovtax)
[1] 1238067
Encontrando que el valor de la varianza para el precio de venta en metros cuadrados sin incluir el garaje, en miles de pesos cuadrados es de \(1238067\).
Desviación estándar
Es la raíz cuadrada de la distancia media del conjunto de datos respeto
a la media, es decir, indica qué tan dispersos se encuentra el conjunto
de observaciones de su valor promedio.
\begin{align*} S=\sqrt{S^2} \end{align*}
En R puede calcularse la desviación estándar de un conjunto de
observaciones mediante la función sd(datos).
Ejercicio Caso de Estudio
Calcule el valor de la desviación estándar asociada a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R de la desviación estándar
asociada al precio de venta en metros cuadrados, se emplea la función
sd(), tal que
sd(datos$preciovtax)
[1] 1112.684
Lo cual significa que en promedio el precio de venta en metros cuadrados, sin incluir el garaje, en miles de pesos es de \(1524.358\), con una desviación estándar de \(1112.684\) miles de pesos.
Coeficiente de variación
Es la desviación estándar como un porcentaje de la media aritmética de
un conjunto de datos. Sirve para observar el grado de variabilidad que
tiene un conjunto de observaciones respecto a su promedio
\begin{align*} CV = \frac{S}{|\bar{X}|} \times 100\% \end{align*}
Entre las funciones base del programa R no hay ninguna función
que calcule el coeficiente de variación de un conjunto de observaciones,
pero éste es fácil de calcular mediante el cociente entre la desviación
estándar $S$ y el valor absoluto de la media $\bar{X}$, o creando
una función que realice el cálculo, de la forma
# Función para el cálculo del coeficiente de variación
CV <- function(x) (sd(x)/abs(mean(x))) * 100
Una vez creada la función, puede calcularse el coeficiente de variación
de un conjunto de observaciones mediante la función CV(datos).
Ejercicio Caso de Estudio
Calcule el coeficiente de variación asociado a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del coeficiente de variación del
precio de venta en metros cuadrados en miles de pesos, sin incluir el
garaje del bien, se emplea la función CV() que se creó
previamente, tal que
### Se crea la función
CV <- function(x) (sd(x)/abs(mean(x))) * 100
### Se realiza el cálculo del coeficiente de variación
CV(datos$preciovtax)
[1] 72.99364
Lo cual significa que el porcentaje de variación del precio de venta por en metros cuadrados, en miles de pesos sin incluir el garaje es del \(72.99%\).
Rango
Es la distancia o amplitud que hay entre el valor máximo y mínimo en un
conjunto de datos \begin{align*} R = x_{max}-x_{min} \end{align*}
Entre las funciones base del programa R no hay ninguna función
que calcule el rango de un conjunto de observaciones de forma directa,,
pero éste es fácil de calcular mediante la resta del valor máximo
max(datos) y mínimo min(datos), o creando una función que realice el
cálculo, de la forma
# Función para el cálculo del rango
Rango <- function(x) max(x) - min(x)
Una vez creada la función, puede calcularse el rango de un conjunto de
observaciones mediante la función Rango(datos). Una forma alternativa
para realizar el cálculo del rango de un conjunto de observaciones, es
empleando una combinaciones de funciones de la forma
diff(range(datos)).
Ejercicio Caso de Estudio
Calcule el rango del asociado a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del rango del precio de venta en
metros cuadrados en miles de pesos, sin incluir el garaje del bien, se
emplea la función Rango() que se creó previamente, tal que
### Se crea la función
Rango <- function(x) max(x) - min(x)
### Se realiza el cálculo del Rango
Rango(datos$preciovtax)
[1] 16552
Lo cual significa que la diferencia entre el precio más alto y el más bajo de venta en metros cuadrados, en miles de pesos sin incluir el garaje es del \(16552\).
Rango intercuartílico
Es la distancia o amplitud que hay entre el tercer cuartil $C_3$ y el
primer cuartil $C_1$, de un conjunto de datos. Éste muestra la
amplitud del 50% de los datos centrales de un conjunto de observaciones.
Esta medida puede ser tomada como una medida de variabilidad para la
mediana. \begin{align*} IQR = C_3 - C_1 \end{align*}
En R puede calcularse el rango intercuartílico de un conjunto
de observaciones mediante la función IQR(datos).
Ejercicio Caso de Estudio
Calcule el rango intercuartílico asociado a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del rango intercuartílico del
precio de venta en metros cuadrados en miles de pesos, sin incluir el
garaje del bien, se emplea la función IQR(), tal que
IQR(datos$preciovtax)
[1] 1110
Lo cual significa que la diferencia entre el \(50\%\) central de los precio de venta en metros cuadrados, en miles de pesos sin incluir el garaje es del \(1110\).
Desviación absoluta mediana
Es una medida de la dispersión de un conjunto de observaciones respecto a su mediana
\begin{align*} MAD=b\times Me(|X_i-\tilde{X}|) \end{align*}
donde $b$ es una constante definida como $b=1/C_{3}$, con $C_{3}$
el valor del tercer cuartil de la distribución de interés (no el
obtenido de los datos) y con $Me(|X_i-\tilde{X}|)$ la mediana del
valor absoluto de la diferencia $X_i-\tilde{X}$. Además, si la
distribución es normal, entonces $b\approx1.4826$.
En R puede calcularse la desviación absoluta mediana de un
conjunto de observaciones, asumiendo que la distribución es normal,
mediante la función mad(datos), si no es posible asumir que la
distribución es normal, entonces puede calcularse mediante la función
mad(datos, constant = b), tal que
Ejercicio Caso de Estudio
Calcule la desviación absoluta mediana asociada a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R de la desviación absoluta mediana
del precio de venta en metros cuadrados en miles de pesos, sin incluir
el garaje del bien, se emplea la función mad(), tal que
mad(datos$preciovtax)
[1] 741.3
Lo cual significa que el precio mediano de venta en metros cuadrados, en miles de pesos sin incluir el garaje es de \(1200\), con una desviación absoluta mediana de \(741.3\) miles de pesos.
Medidas de forma
Estas medidas tienen por objetivo evidenciar si el conjunto de observaciones tiene o no una forma simétrica y observar su nivel de concentración.
Coeficiente de asimetría
Este valor permite identificar si el conjunto de datos se distribuye
uniformemente alrededor de las medidas de tendencia central.
\begin{align*} \gamma_1 = \frac{1}{n}\frac{\sum_{i=1}^n{(x_i-\bar{X})^3}}{S^3} \quad \quad -\infty<\gamma_1<\infty \end{align*}
El signo de $\gamma_1$ indica la dirección de la asimetría.
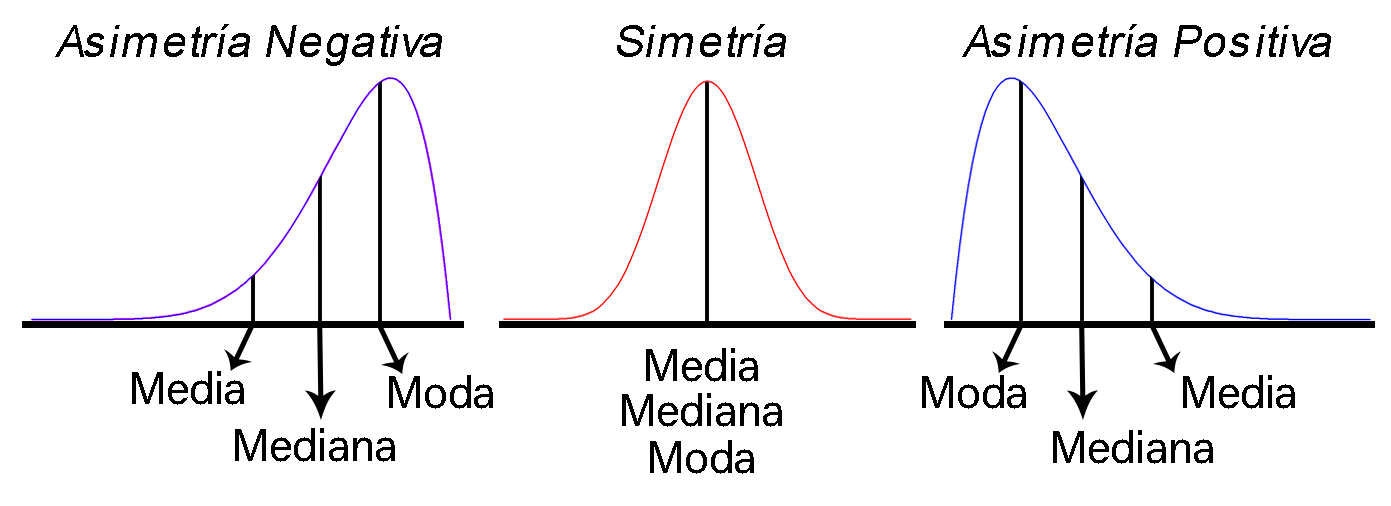
$\gamma_1>0$indica asimetría positiva, es decir, las observaciones se reúnen más en la parte izquierda de las medidas de tendencia central.$\gamma_1<0$indica asimetría negativa, es decir, las observaciones se reúnen más en la parte derecha de las medidas de tendencia central.$\gamma_1\sim0$indica simetría, es decir, existe aproximadamente la misma cantidad de observaciones a los dos lados de las medidas de tendencia central.
Representación tipos de Asimetría
Entre las funciones base del programa R no hay ninguna función
que calcule el coeficiente de asimetría de un conjunto de observaciones,
pero es posible realizar el cálculo mediante la función
skewness(datos) de la librería e1071.
Ejercicio Caso de Estudio
Calcule el coeficiente de asimetría asociada a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del coeficiente de asimetría del
precio de venta en metros cuadrados en miles de pesos, sin incluir el
garaje del bien, se emplea la función skewness() de la
librería e1071, tal que
# Se carga la librería
library(e1071)
# Se realiza el cálculo del coeficiente de asimetría
skewness(datos$preciovtax)
[1] 2.396478
Lo cual significa que el coeficiente de asimetría del precio de venta en metros cuadrados, en miles de pesos sin incluir el garaje es de \(2.3964\), lo cual significa que al ser positivo, quiere decir que es más probable que los precios de venta se encuentren más reunidos para precios bajos, y que los precios altos son menos probables.
Coeficiente de exceso de curtosis
Este valor permite observar el grado de concentración del conjunto de
datos
\begin{align*} \gamma_2 = \frac{1}{n}\frac{\sum_{i=1}^n{(x_i-\bar{X})^4}}{S^4}-3 \quad \quad -2<\gamma_2<\infty \end{align*}
El signo de $\gamma_2$ indica el nivel de concentración.
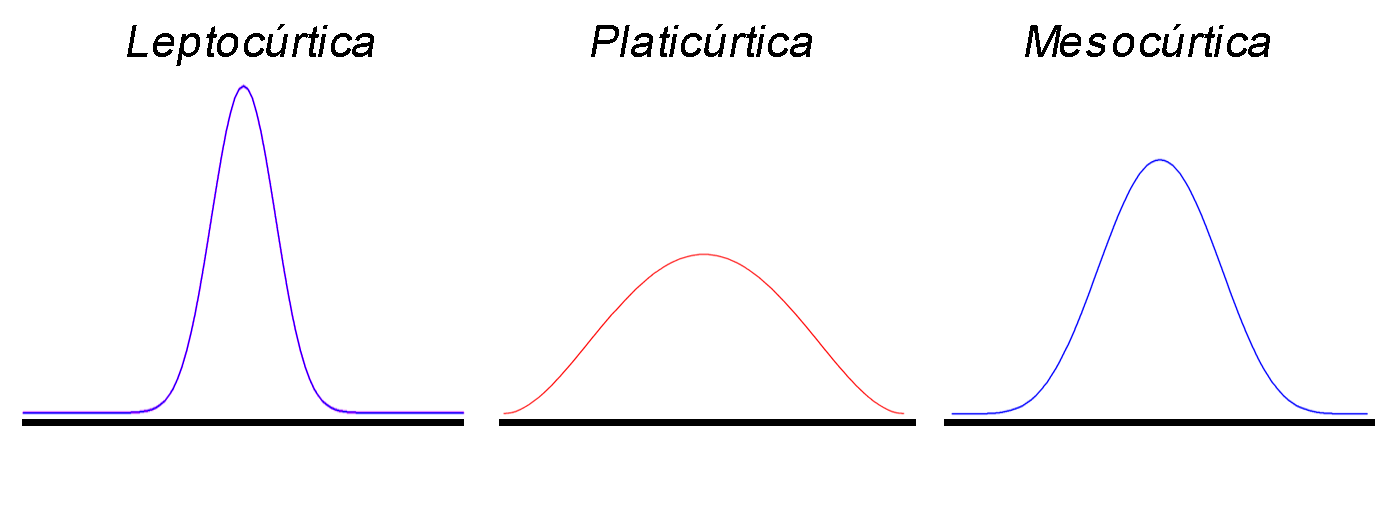
$\gamma_2>0$indica leptocurtosis, es decir, la forma de los datos es más en punta y posee colas menos anchas.$\gamma_2<0$indica platicurtosis, es decir, la forma de los datos es más plana y posee colas más anchas.$\gamma_2\sim0$indica mesocurtosis, es decir, tanto la punta como las colas son similares a la distribución normal.
Representación tipos de kurtosis
Entre las funciones base del programa R no hay ninguna función
que calcule el coeficiente de exceso de curtosis de un conjunto de
observaciones, pero es posible realizar el cálculo mediante la función
kurtosis(datos) de la librería e1071.
Ejercicio Caso de Estudio
Calcule el coeficiente de exceso de curtosis asociada a la variable precio de venta en metros cuadrados preciovtax.
Solución en R
Para realizar el cálculo en R del coeficiente de exceso de
curtosis del precio de venta en metros cuadrados en miles de pesos, sin
incluir el garaje del bien, se emplea la función kurtosis()
de la librería e1071, tal que
# Se carga la librería
library(e1071)
# Se realiza el cálculo del coeficiente de exceso de curtosis
kurtosis(datos$preciovtax)
[1] 9.817481
Lo cual significa que el coeficiente de exceso de curtosis del precio de venta en metros cuadrados, en miles de pesos sin incluir el garaje es de \(9.817481\), lo cual significa que al ser un valor positivo, quiere decir que es la forma de los precios de venta es leptocurtica, es decir, que los datos se encuentran más reunidos y la forma de la distribución tiene forma punteaguda.
Medidas de asociación
Estas medidas tienen por objetivo estimar la magnitud con la que dos
fenómenos se relacionan, en donde, entre mayor sean estas medidas, mayor
será el grado de asociación que tendrán las variables. Si se define
$x_1, x_2, \ldots, x_n$ y $y_1, y_2, \ldots, y_n$ como dos conjuntos
de $n$ observaciones, entonces
Covarianza
Mide si existe o no dependencia lineal entre las variables, e indica el
grado de variación conjunta de dos variables respecto a sus medias
\begin{align*} S_{xy} = \frac{1}{n}\sum_{i=1}^n{(x_i-\bar{X})(y_i-\bar{Y})} \end{align*}
El signo de $S_{xy}$ indica el tipo de dependencia lineal que hay
entre las variables.
$S_{xy} > 0$indica que hay dependencia lineal positiva entre las variables, es decir, cuando aumenta una variable, la otra también aumenta.$S_{xy} < 0$indica que hay dependencia lineal negativa entre las variables, es decir, cuando aumenta una variable, la otra disminuye.$S_{xy} \approx 0$indica que no existencia dependencia lineal entre las dos variables.
En R puede calcularse la covarianza de dos conjunto de
observaciones mediante la función cov(datos1, datos2).
Ejercicio Caso de Estudio
Calcule la covarianza que existe entre la variable precio de venta en metros cuadrados preciovtax y la variable del metros cuadrados de la unidad de garaje areaunitga.
Solución en R
Para realizar el cálculo en R del coeficiente de covarianza que
existe entre las variables preciovtax y areaunitga, se
emplea la función cov(), tal que
cov(datos$preciovtax, datos$areaunitga)
[1] 1806.643
Lo cual significa que la covarianza entre la variable precio de venta en metros cuadrados preciovtax y la variable del metros cuadrados de la unidad de garaje areaunitga es de \(1806.643\), y por tanto, como dicho valor es positivo significa que existe una dependencia lineal positiva entre estas dos variables.
Correlación
Mide la fuerza de la dependencia lineal que hay entre variables, esta va
entre -1 y 1
\begin{align*} \rho_{xy} = \frac{S_{xy}}{S_{x}S_{y}} \quad \quad -1<\rho_{xy}<1 \end{align*}
El valor de $\rho_{xy}$ indica el tipo y fuerza de la dependencia
lineal que hay entre las variables
$\rho_{xy} = 1$indica que existe dependencia lineal positiva exacta entre las variables, es decir, cuando aumenta una variable, la otra aumenta proporcionalmente en la misma cantidad. Este aumento es de la forma$Y = a + bX$, siendo$a$y$b$dos constantes, con$b>0$.$\rho_{xy} = -1$indica que existe dependencia lineal negativa exacta entre las variables, es decir, cuando aumenta una variable, la otra disminuye proporcionalmente en la misma cantidad. Este aumento es de la forma$Y = a + bX$con$a y b$dos constantes, y$b<0$.$\rho_{xy} = 0$No existe dependencia lineal entre las variables.
Además, se tendrá que si
$0.5 < \rho_{xy} \leq 1$fuerte correlación positiva entre$X$y$Y$.$0.3 < \rho_{xy} \leq 0.5$moderada correlación positiva entre$X$y$Y$.$0.1 < \rho_{xy} \leq 0.3$débil correlación positiva entre$X$y$Y$.$-0.1 \leq \rho_{xy} \leq 0.1$débil o ninguna correlación entre$X$y$Y$.$-0.3 \leq \rho_{xy} < -0.1$débil correlación negativa entre$X$y$Y$.$-0.5 \leq \rho_{xy} < -0.3$moderada correlación negativa entre$X$y$Y$.$-1 \leq \rho_{xy} < -0.5$fuerte correlación negativa entre$X$y$Y$.
En R puede calcularse la correlación de dos conjunto de
observaciones mediante la función cor(datos1, datos2).
Ejercicio Caso de Estudio
Calcule la correlación que existe entre la variable precio de venta en metros cuadrados preciovtax y la variable del metros cuadrados de la unidad de garaje areaunitga.
Solución en R
Para realizar el cálculo en R la correlación que existe entre
las variables preciovtax y areaunitga, se emplea la
función cor(), tal que
cor(datos$preciovtax, datos$areaunitga)
[1] 0.4419193
Lo cual significa que la correlación que exite entre la variable precio de venta en metros cuadrados preciovtax y la variable del metros cuadrados de la unidad de garaje areaunitga es del \(44.19%\), lo cual significa que hay una relación lineal positiva moderada entre estas dos variables.