Intervalos de confianza para razón de varianzas $\sigma^2_1/\sigma^2_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias normales
de tamaños $n_1$, y $n_2$ con medias $\mathbb{E}(X_{1})=\mu_1$ y
$\mathbb{E}(X_{2})=\mu_2$, y varianzas desconocidas
$Var(X_{1})=\sigma_1^2<\infty$ y $Var(X_{2})=\sigma^2_2<\infty$,
respectivamente, entonces un intervalo de confianza del
$100(1-\alpha)\%$ para $\sigma^2_1/\sigma^2_2$ estará dada por

Ejercicio
Se aplican pruebas a \(10\) cables conductores soldados a un dispositivo semiconductor con el fin de determinar su resistencia a la tracción. Las pruebas demostraron que para romper la unión se requiere las libras de fuerza que se listan a continuación.
| Sin Encapsulado | 19.8 | 12.7 | 13.2 | 16.9 | 10.6 | 18.8 | 11.1 | 14.3 | 17.0 | 12.5 |
Otra conjunto de \(8\) cables conductores que forman otro dispositivo, se encapsulan y se prueban para determinar si el encapsulado aumenta la resistencia a la tracción, obteniendo para este caso se requirieron las siguientes libras de fuerza para romper la unión
| Con Encapsulado | 24.9 | 22.9 | 23.6 | 22.1 | 20.3 | 21.6 | 21.9 | 22.5 |
Si se supone que las resistencias a la tracción se distribuyen normalmente, construya un intervalo del \(90\%\) para la razón de varianzas entre la variabilidad de los cables sin encapsulado y la variabilidad de los cables con encapsulado. Es posible afirmar que la variabilidad de de los cables con encapsulado es superior a los cables sin encapsulado?
Solución
En este punto nos mencionan que se tiene interés en calcular un
intervalo de confianza para el cociente de las varianzas asociadas a la
resistencia a la tracción para cables sin encapsulado y cables con
encapsulado. Además nos mencionan que la resistencia a la tracción hasta
la ruptura se distribuye normalmente, y por tanto deberemos calcular el
siguiente intervalo

en donde se aprecia que el intervalo bilateral para la razón de
varianzas posee la estructura \[\begin{align*}
\frac{S^2_C}{S^2_S}\frac{1}{f_{\alpha/2, n_C-1, n_S-1}} < \frac{\sigma^2_C}{\sigma^2_S} < \frac{S^2_C}{S^2_S}f_{\alpha/2, n_S-1, n_C-1}
\end{align*}\]
En donde se observa que para realizar el cálculo del intervalo, se
requiere de los varianzas muestrales \(S^2_S\) y \(S^2_C\), el nivel de
confianza \(1-\alpha\) y los valores críticos
\(f_{\alpha/2, n_C-1, n_S-1}\) y \(f_{\alpha/2, n_S-1, n_C-1}\).
Para realizar el cálculo de las varianzas muestrales, se emplean
los datos muestrales y los tamaños de muestra \(n_C=8\) y \(n_S=10\),
tal que al realizar el cálculo obtenemos
\[\begin{align*}
S^2_C &= 1.899286 \\
S^2_S &= 10.441
\end{align*}\]
Por su parte, al buscar los valores críticos para un nivel de
significancia \(1-\alpha=0.90\) y tamaños muestrales \(n_C=8\) y
\(n_S=10\) tenemos que
\[\begin{align*}
f_{\alpha/2 = 0.05, n_C-1 = 7, n_S-1 = 9} &= 3.292746\\
f_{\alpha/2 = 0.05, n_S-1 = 9, n_C-1 = 7} &= 3.676675
\end{align*}\]
Una vez calculados los valores necesarios para calcular el intervalo de
confianza, se procede a su cálculo, tal que \[\begin{align*}
\frac{1.899286}{10.441}\frac{1}{3.292746} &< \frac{\sigma^2_C}{\sigma^2_S} < \frac{1.899286}{10.441}3.676675 \\
0.05524463 &< \frac{\sigma^2_C}{\sigma^2_S} < 0.6688112
\end{align*}\]
Por tanto, se podrá concluir con un nivel de confianza del \(90\%\) que
el verdadero valor para el cociente de varianzas entre la variabilidad
de los cables sin encapsulado y la variabilidad de los cables con
encapsulado, se encontrará entre \(0.05524463\) y \(0.6688112\).
Ahora, para verificar si existen o no diferencias significativas
entre las varianzas de resistencia a la tracción de los cables
encapsulados o sin encapsular, debemos verificar la posición en la que
se encuentra el intervalo de confianza para la razón de varianzas
\(\sigma^2_C/\sigma^2_S\).
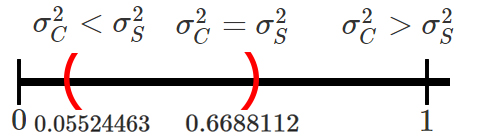
En donde se observa que el intervalo calculado no contiene el valor
de \(1\), el cual representa la igualdad entre la varianza de los dos
tipos de cable, tal que \[\begin{align*}
\sigma^2_C = \sigma^2_S \quad =>\quad \frac{\sigma^2_C}{\sigma^2_S} = 1
\end{align*}\]
y por tanto, con un nivel de confianza del \(90\%\) será posible afirmar
que la variabilidad de la resistencia a la tracción de los cables
encapsulados o sin encapsular son diferentes, y por tanto, debe asumirse
que NO son iguales.