Estimación por intervalos
Podría ser que ni el estimador que cumpla las propiedades de insesgadez, eficiencia, consistencia y suficiencia, estimen con exactitud el parámetro poblacional de interés- Por esta razón, puede ser preferible determinar un intervalo dentro del cual, se espera encontrar el valor verdadero del parámetro poblacional.
Definición
Sea $\theta$ un parámetro poblacional desconocido, entonces basándose
en la información de una muestra aleatoria de dicha población, el
objetivo será encontrar dos variables aleatorias $\hat{\Theta}_I$ y
$\hat{\Theta}_S$ tal que
\begin{align*} \mathbb{P}(\hat{\Theta}_I<\Theta<\hat{\Theta}_S) = 1-\alpha \quad \quad 0<\alpha<1 \end{align*}
donde $(1-\alpha)$ se conoce como nivel de confianza y
$\hat{\Theta}_I$ y $\hat{\Theta}_S$ se denominan como límites de
confianza inferior y superior, tal que
$\hat{\Theta}_I<\hat{\Theta}_S$.
Nota
- Usualmente se usan valores para \(\alpha\) de \(0.1, 0.05\) y $ 0.01$, es decir, niveles de confianza de \(0.9, 0.95\) y \(0.99\).
- La longitud o amplitud del intervalo construido, medirá la precisión de la estimación realizada, por tanto, intervalos largos proporcionan estimaciones más imprecisas, mientras que intervalos cortos proporcionan estimaciones más precisas.
- A medida que aumenta el nivel de confianza, la amplitud del intervalo se hace más grande.
- A medida que aumenta el tamaño de muestra, la amplitud del intervalo se hace más pequeño.
Interpretación de nivel de confianza
El nivel de confianza, $1-\alpha$, mide la fiabilidad del intervalo de
probabilidad, esto es, la probabilidad de que el verdadero valor del
parámetro se encuentre dentro del intervalo construido. Es decir, que si
se realiza el experimento muchas veces, se tendrá que en el
$100(1-\alpha)\%$ de los intervalos de confianza construidos en cada
experimento, se encontrará contenido el verdadero valor del parámetro de
interés.
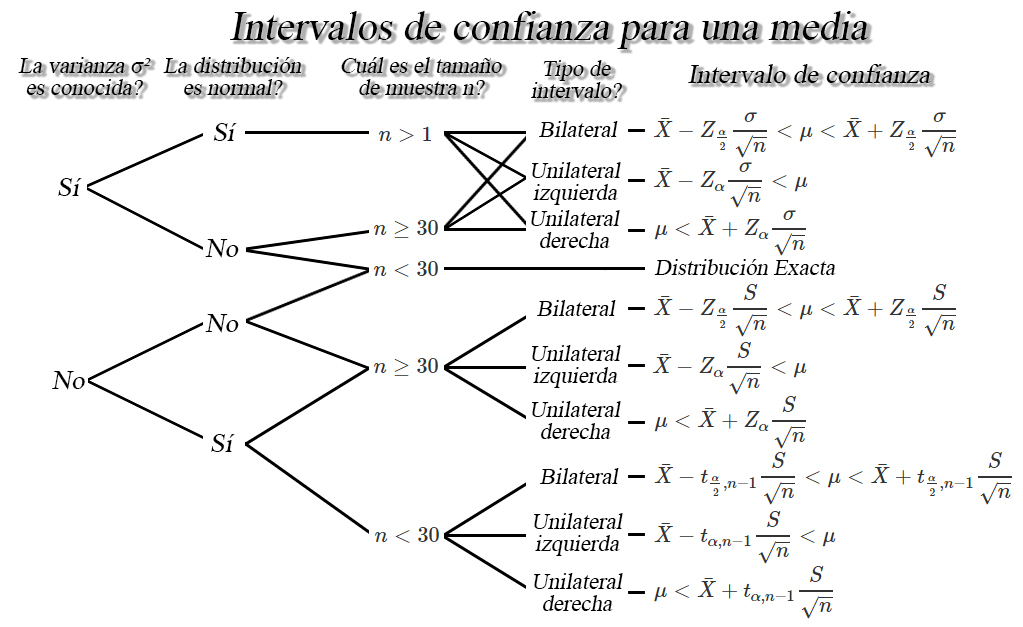
Intervalos de confianza para una media $\mu$
Sea $X_1, X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$ con media desconocida $\mathbb{E}(X)=\mu$, y varianza
$Var(X)=\sigma^2<\infty$, entonces dependiendo de las condiciones, se
tendrán los siguientes intervalos de confianza para la media $\mu$.
Ejercicio
Suponga que se realiza un estudio sobre el salario de los estudiantes de Ingeniería Industrial una vez finalizan su pregrado y se incertan en el mercado laboral. Para ello, se le pregunta a \(15\) egresados seleccionados de forma aleatoria y se les pregunta cuál es el salario que devengan actualmente, obteniendo los siguientes resultados en millones de pesos \[\begin{align*} 1.78 \quad 2.93 \quad 1.22 \quad 1.27 \quad 1.17 \\ 1.03 \quad 1.24 \quad 2.07 \quad 2.04 \quad 1.28 \\ 1.53 \quad 0.98 \quad 1.73 \quad 1.38 \quad 3.24 \end{align*}\] Si es posible supone que los salarios de los egresados se distribuyen aproximadamente normal, calcule el límite superior del salario promedio que ganan los egresados del programa de ingeniería industrial empleando un nivel de confianza del \(98\%\).
Solución
En este caso estamos interesados en construir un intervalo de confianza
para el límite superior de los salarios promedio de los egresados, pero
para realizar el cálculo debemos tener en cuenta la información que
poseemos.
De la información extraída del enunciado tenemos que
la varianza poblacional no es conocida, ya que no la mencionan en el
enunciado, tenemos que la población es normal, debido a que mencionan
que puede suponerse que los salarios son aproximadamente normales, y los
tamaños de muestra son pequeños, debido a que solo tenemos \(15\) datos,
estas características se ilustra en la siguiente imagen
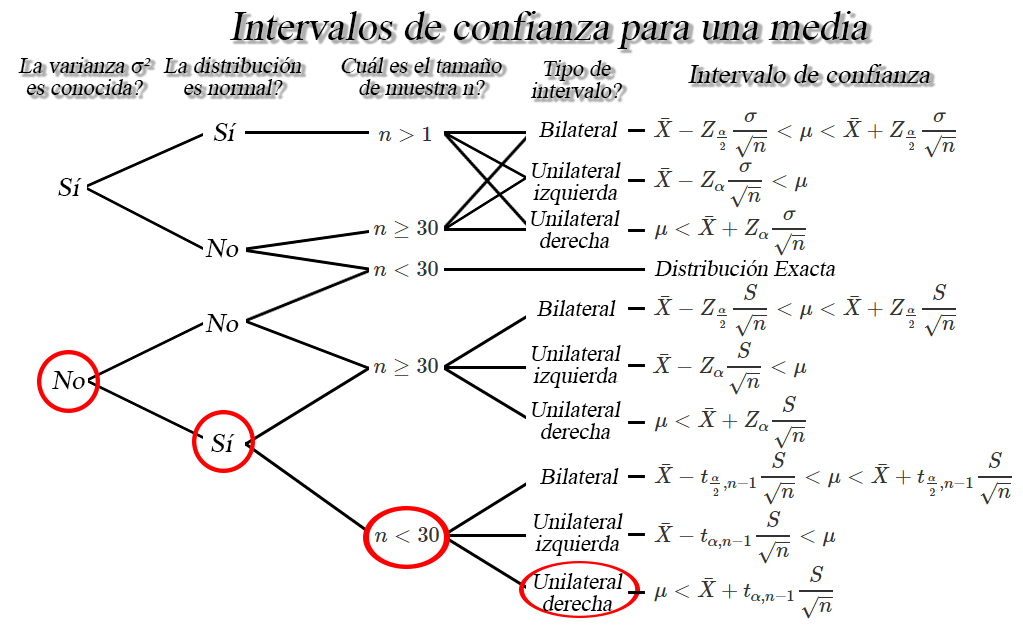de lo anterior encontramos que el intervalo de confianza de interés es
de la forma \[\begin{align*}
\mu < \bar{X}+t_{\alpha, n-1}\frac{S}{\sqrt{n}}
\end{align*}\]
En donde observamos que requerimos de \(5\) variables, la media muestral
\(\bar{X}=1.659333\), la desviación estándar muestral \(S=0.6709425\),
el tamaño de muestra \(n=15\), el nivel de confianza \(1-\alpha=0.98\) y
el valor crítico \(t_{\alpha=0.02, n-1=14}=2.263781\) calculado a partir
del nivel de confianza y el tamaño de la muestra. Al reemplazar en el
intervalo tenemos que \[\begin{align*}
\mu &< 1.659333+2.263781\frac{0.6709425}{\sqrt{15}}\\
\mu &< 1.659333+0.3921697\\
\mu &< 2.051503
\end{align*}\]
Entonces podremos afirmar con un nivel de confianza del \(98\%\), que el
salario máximo promedio que ganan los egresados del Departamento de
Ingeniería Industrial es de \(2.051503\) millones de pesos, es decir,
dos millones cincuenta y un mil quinientos tres pesos.
Ejercicio
Suponga que Postobon desarrolla una nueva máquina de bebidas para servir
de forma automática gaseosas en los cines, de tal forma que la cantidad
servida, en mililitros, se distribuya Weibull con desviación estándar de
\(5703.473_{ml}\).
Si se decide tomar una muestra aleatoria de
\(8000\) vasos de gaseosa servidos por una de las nuevas máquinas de
bebidas, y se obtiene una promedio de \(345_{ml}\) con una desviación
estándar de \(5240.35_{ml}\), construya un intervalo de confianza del
\(90\%\) para la verdadera cantidad promedio de refresco servida por la
máquina.
Solución
En este caso estamos interesados en construir un intervalo de confianza
bilateral del $90% $ para la cantidad promedio de refresco servida por
la nueva máquina de bebidas, pero para realizar el cálculo debemos
evaluar previamente la información que poseemos.
Del contexto
del ejercicio tenemos que la población no es normal, debido a que se
menciona que es Weibull, con desviación estándar de \(5703.473_{ml}\),
por lo cual tendremos que la varianza poblacional es conocida.
Adicionalmente, tenemos que el tamaño de muestra de vasos de gaseosa
servidos por la máquina es de \(8000\) vasos, por lo cual, basados en la
información que poseemos tenemos las siguientes características
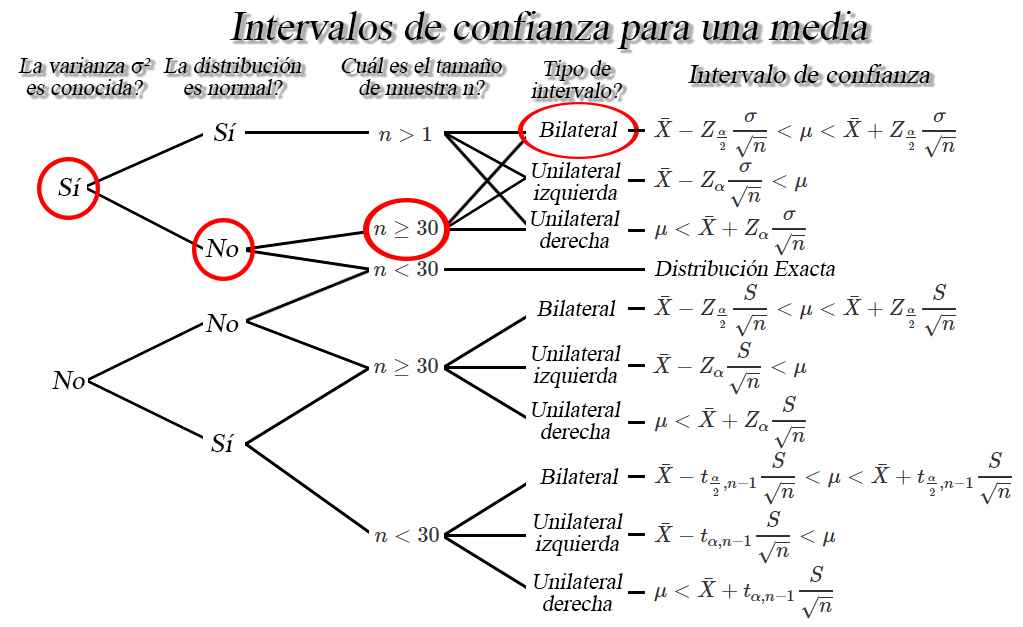de lo anterior encontramos que el intervalo de confianza de interés es
de la forma \[\begin{align*}
\bar{X}-Z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}} < \mu < \bar{X}+Z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}
\end{align*}\]
En donde observamos que requerimos la media muestral \(\bar{X}=345\), la
desviación estándar poblacional \(\sigma=5703.473\), el tamaño de
muestra \(n=8000\), el nivel de confianza \(1-\alpha=0.90\) y el valor
crítico \(Z_{\alpha/2=0.05}=1.644854\) calculado a partir del nivel de
confianza. Al reemplazar en el intervalo tenemos que \[\begin{align*}
&345\pm 1.644854 \frac{5703.473}{\sqrt{8000}} \\
&345\pm 104.8870143 \\
&240.1129856 < \mu < 449.8870144
\end{align*}\]
Entonces podremos afirmar con un nivel de confianza del \(90\%\), que la
cantidad promedio de refresco servida de forma automática por la nueva
máquina de bebidas se encontrará entre \(240.1129_{ml}\) y
\(449.8870_{ml}\).
Ejercicio
Suponga que la marca de cigarrillo Malboro, asegura que el contenido
promedio de nicotina de sus cigarrillos es de \(1.1\) miligramos. Un
estudio realizado por un grupo de investigación de la Universidad de
Antioquia mide el contenido de nicotina de una muestra aleatoria de
\(145\) cigarrillos y encuentra que la nicotina promedio y desviación
estándar de la muestra fue de \(1.02\) y \(0.23\) miligramos de
nicotina, respectivamente.
Si se supone que la cantidad de
nicotina en los cigarrillos Malboro se distribuye normalmente, calcule
con un nivel de confianza del \(85\%\) el límite inferior para la
verdadera cantidad promedio de nicotina que poseen los cigarrillos
Malboro.
Solución
En este ejercicio se está interesado en construir un intervalo de
confianza inferior del \(85\%\) para la cantidad promedio de nicotina
que poseen los cigarrillos Malboro, y para realizar el cálculo debemos
evaluar la información que poseemos.
En donde, basados en el
contexto del ejercicio nos dicen que la distribución de probabilidad de
la cantidad de nicotina de los cigarrillos se distribuye normalmente,
con varianza poblacional desconocida. Además, mencionan que en un
estudio realizado por un grupo de investigación se toma una muestra
aleatoria de tamaño \(145\) cigarrillos, a partir de la cual encuentran
un contenido promedio de nicotina de \(1.02\) miligramos con una
desviación estándar de \(0.23\) miligramos, y en consecuencia nos
encontramos en la siguiente situación
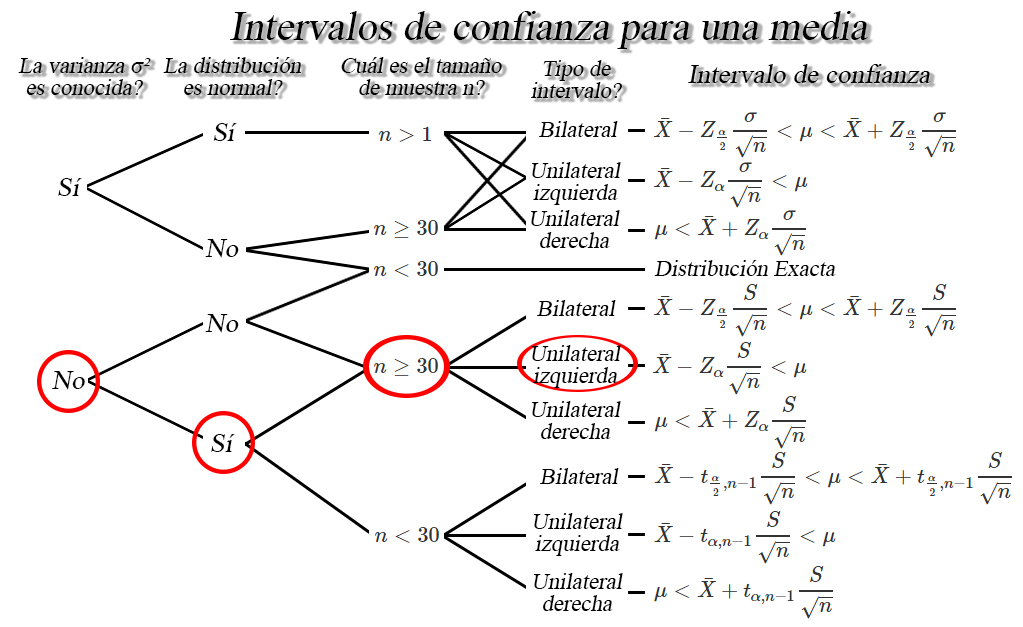de lo anterior encontramos que el intervalo de confianza de interés es
de la forma \[\begin{align*}
\bar{X}-Z_{\alpha}\frac{S}{\sqrt{n}} < \mu
\end{align*}\]
En donde observamos que necesitamos la media muestral \(\bar{X}=1.02\),
la desviación estándar muestral \(S=0.23\), el tamaño de muestra
\(n=145\), el nivel de confianza \(1-\alpha=0.85\) y el valor crítico
\(Z_{\alpha=0.15}=1.036433\) calculado a partir del nivel de confianza.
Al reemplazar en el intervalo de interés tenemos que \[\begin{align*}
1.02-1.036433\frac{0.23}{\sqrt{145}} &< \mu \\
1.02-0.01979635 &< \mu \\
1.000204 &< \mu
\end{align*}\]
Lo cual significa que, con un nivel de confianza del \(85\%\) podemos
afirmar que la cantidad mínima promedio de nicotina que poseen los
cigarrillos Malboro es de \(1.000204\) miligramos de nicotina.