Introducción a R
R es un lenguaje de programación interpretado orientado a objetos junto con un sistema de ventanas, que permite una interacción directa e intuitiva con el tipo de programación realizada. Este tipo de programación, posee una notable cercanía con la forma en que se expresarían las cosas en la vida real, ya que trabaja sobre objetos visibles que poseen determinadas característica, lo cual hace que puedan ser empleados para la realización de acciones específicas.
Para entender cómo se crean o manipulan objetos en R, es necesario introducir inicialmente el lenguaje de programación, y para ello lo primero que debe hacerse, es entender la estructura de asignación, los tipos de datos, las clases de los objetos y los tipos de operadores
Estructura de asignación
La estructura de asignación del lenguaje R puede llevarse a cabo mediante cuatro formas diferentes, donde, cada una de ellas lleva al mismo resultado
variable <- objeto # Primer método
objeto -> variable # Segundo método
variable = objeto # Tercer método
assign(variable, objeto) # Cuarto método
De estos cuatro métodos de asignación presentados, el primero y el segundo poseen la misma estructura, la diferencia entre ellos radica en que, el primero realiza la asignación a la izquierda y el segundo a la derecha, lo cual depende de la dirección hacia donde apunte la flecha.
El tercer método, a pesar de realizar la asignación al igual que los dos primeros métodos, éste no es el operador habitual de asignación, pues éste se encuentra reservado para otros propósitos, tales como darle valores a una variable dentro de una función. El cuarto método, es una forma de asignación equivalente a las dos primeras, pero requiere de “más esfuerzo” para llevarse acabo la asignación.
Por lo tanto, se recomienda emplear el primer método de asignación.
Es de anotar que el símbolo <- puede escribirse de dos formas,
presionando la tecla < seguida de la tecla -, o alternativamente,
presionando de forma simultanea las teclas Alt y la tecla -.
También se señala que el carácter #, se emplea para comentar el
código o una línea específica, lo cual implica que posterior a #, no
se ejecutará ningún tipo de código en la linea específica en la cual se
encuentre #.
Tipo de datos
Existen diferentes tipos de datos en los lenguajes de programación, de estos tipos dependerá las operaciones o funciones que pueden o no emplearse con éstos, y es por ello que debe tenerse especial cuidado cuando se deseen manipular.
Los tipos de datos más que pueden encontrarse en R son:
- numeric: Datos numéricos, los cuales soportan números
que se encuentren en el conjunto de los reales,
$\mathbb{R}$, y por tanto soporta tanto números enteros (integer) y números de doble precisión (double). - integer: Datos enteros, los cuales soportan números que
se encuentren en el conjunto de los enteros,
$\mathbb{Z}$, y en consecuencia, solo soporta números enteros. - complex: Datos complejos, los cuales soportan números
que se encuentren en el conjunto de los complejos,
$\mathbb{C}$, y por tanto, soporta tanto números reales como imaginarios. - character: Datos de carácter, los cuales soportan caracteres alfanuméricos, es decir, datos numéricos y alfabéticos. Éstos deben ser escritos entre comillas simples o dobles.
- factor: Datos categóricos nominales, los cuales soportan caracteres alfanuméricos, y establece entre estos diferentes categorías. Se puede emplear la función factor() para crear datos de este tipo. Éstos deben ser escritos entre comillas simples o dobles.
- ordered: Datos categóricos ordinales, los cuales soportan caracteres alfanuméricos, y establece entre estos diferentes categorías junto con una estructura jerárquica. Se puede emplear la función ordered() para crear datos de este tipo. Éstos deben ser escritos entre comillas simples o dobles.
- logical: Datos lógicos, los cuales soportan caracteres lógicos tales como TRUE o FALSE.
Para verificar al estructura de almacenamiento en R, puede emplearse la función str(), mientras para observar la estructura de almacenamiento pueden emplearse las funciones mode(), typeof, y para observar la clase interna del objeto puede emplearse la función class().
A continuación se presenta un ejemplo en donde se muestran los diferentes tipos de objetos en R
Dato tipo numérico
# Numeric
a <- 3.3
str(a)
num 3.3
Dato tipo entero
# Integer
b <- 3L
str(b)
int 3
Dato tipo lógico
# Complex
c <- 3 + (0+0.2i)
str(c)
cplx 3+0.2i
Dato tipo carácter
# Character
d <- "Ejemplo :D"
str(d)
chr "Ejemplo :D"
Dato tipo factor
# Factor
e <- factor("Otro ejemplo :o")
str(e)
Factor w/ 1 level "Otro ejemplo :o": 1
Dato tipo ordinal
# Ordered
f <- ordered("Uno más >:o")
str(f)
Ord.factor w/ 1 level "Uno más >:o": 1
Dato tipo lógico
# logic
g <- FALSE
str(g)
logi FALSE
Clases de objetos
Adicionalmente, con el fin de organizar los datos, se presentan algunas de las clases de objetos más comúnmente usados en R
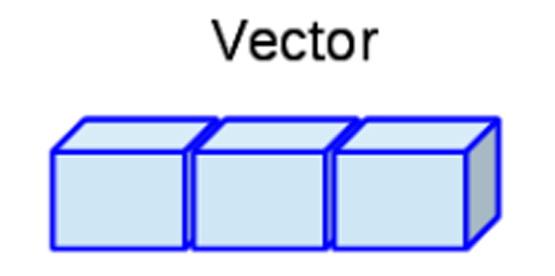
- Vector: este objeto admite datos numéricos, caracteres,
complejos o lógicos, pero solo permite un solo tipo de dato a la
vez. Puede construirse mediante la función
c().
Representación de un Vector
Solución en R
vecN <- c(1, 4, 5, -6.2, 2, -3) # Númerico
vecC <- c("a", "c", "a", "b", "c", "a") # Alfanumérico
vecL <- c(F, T, NA, F, T, F) # Lógico
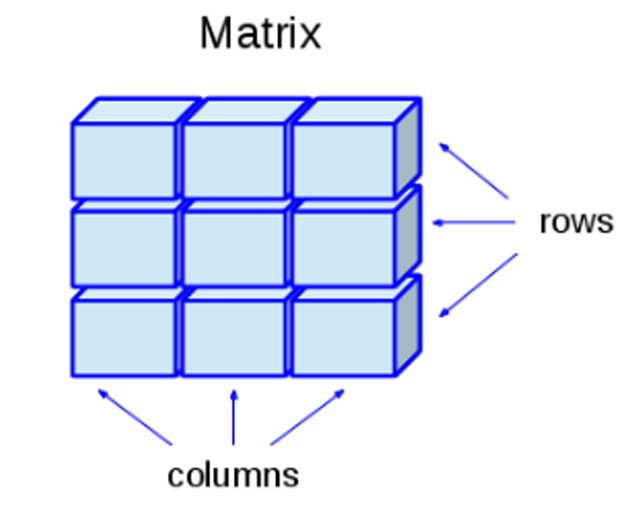
- Matriz: este objeto admite datos numéricos, caracteres,
complejos o lógicos, pero solo permite un solo tipo de dato a la
vez. Puede construirse mediante la función
matrix().
Representación de un Matriz
Solución en R
matN <- matrix(data = c(1, 4, 5, 6, 2, 3), nrow = 3, ncol = 2, byrow = T) # Númerico
matC <- matrix(data = c("a", "c", "a", "b", "c", "a"), nrow = 2, ncol = 3, byrow = F) # Alfanumérico
matL <- matrix(data = c(vecL, T, T, F), nrow = 3, ncol = 3, byrow = F) # Lógico
rownames(matN) <- c("F1", "F2", "bla") # Poner nombre filas
colnames(matN) <- c("D:", "C2") # Poner nombre columnas
matV <- matrix(data = c(-5, -6, 8.1, 12.3, 2, -1), nrow = 1) # Crear vector con función matrix
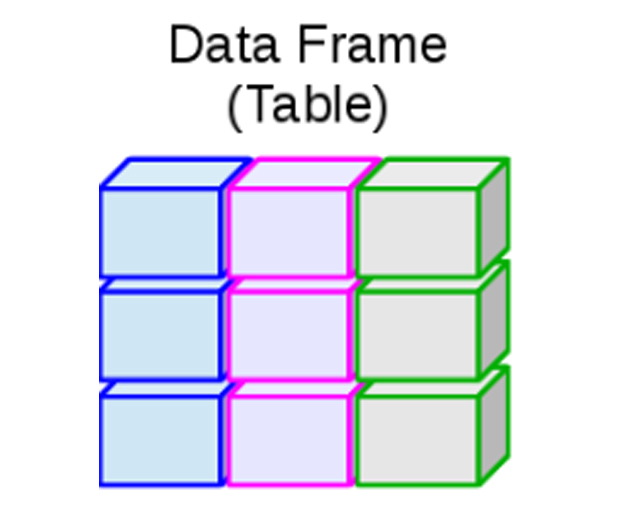
- Marco de Datos: Permite datos numéricos, caracteres, complejos o
lógicos, además de permitir múltiples tipos por objeto a la vez.
Puede construirse mediante la función
data.frame().
Representación de un Marco de Datos
Solución en R
dataf <- data.frame(cbind(vecN, vecC, vecL))
# Las funciones cbind() y rbind() combinan vectores, matrices o data-frame
# por columna o fila, respectivamente.
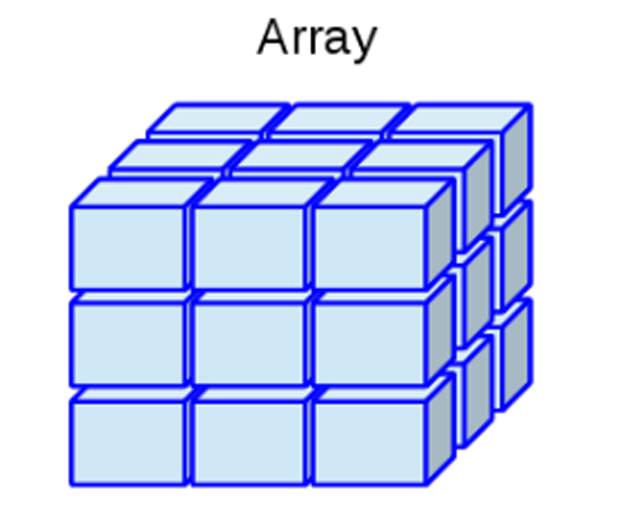
- Arreglos: Permite datos numéricos, caracteres, complejos o
lógicos, pero solo permite un solo tipo de dato a la vez. Puede
construirse mediante la función
array().
Representación de un Arreglo
Solución en R
arrN <- array(data = c(1, 4, 5, 6, 2, 3, 2, 3, 4, 1, 2, 4), dim = c(3, 2, 2)) # Númerico
arrC <- array(data = c(vecC, "o", "m"), dim = c(2, 2, 2)) # Alfanumérico
arrL <- array(data = c(vecL, F, F, NA, F, T, NA), dim = c(2, 2, 3)) # Lógico
arrV <- array(data = c(-5, -6, 8.1, 12.3, 2, -1)) # Crear vector con función array
arrM <- array(data = vecC, dim = c(2, 3, 1)) # Crear matriz con función array
- Listas: Permite datos numéricos, caracteres, complejos, lógicos,
funciones, expresiones, etc, además de permitir múltiples tipos por
objetos a la vez. Puede construirse mediante la función
list().
Representación de listas
Solución en R
listica <- list(dataf, matN, expression(beta))
Operadores aritméticos y precedencias
Existen diferentes operadores aritméticos que pueden emplearse en los lenguajes de programación. Estos se resumen en la siguiente tabla.
| Operación | Operador en R | Asociatividad | Precedencia |
|---|---|---|---|
| Potencia | ^ | Por la derecha | 1 |
| Producto | * | Por la izquierda | 2 |
| División | / | Por la izquierda | 2 |
| División Entera | %/% | Por la izquierda | 2 |
| Módulo o Resto | %% | Por la izquierda | 2 |
| Suma | + | Por la izquierda | 3 |
| Resta | - | Por la izquierda | 3 |
Como se observa, existen operadores que poseen el mismo nivel de prioridad, y por tanto éstos se ejecuta de izquierda a derecha. Para evitar problemas en los cálculos para operadores del mismo nivel de precedencia, se aconseja emplear el paréntesis, con el fin de modificar el orden de las operaciones.
Operadores lógicos
También es posible que se quieran realizar operaciones lógicas entre objetos cuando se realiza programación en los diferentes lenguajes, ya sea para establecer condicionales, o para hacer algunas verificaciones. Estos se resumen en la siguiente tabla.
| Operación | Operador en R | Precedencia |
|---|---|---|
| Igual que | == | 4 |
| Distinto que | != | 4 |
| Menor que | < | 4 |
| Menor o igual que | <= | 4 |
| Mayor que | > | 4 |
| Mayor o igual que | >= | 4 |
| Conjunción | & | 5 |
| Disyunción | | | 5 |
| Negación | ! | 6 |
| Asignación | <- | 7 |
Funciones matemáticas
Hay una gran variedad de funciones matemáticas que suelen usarse en la práctica, y es por ello que se listan las funciones aritméticas que suelen emplearse comúnmente por lenguaje de programación. Estos se resumen en la siguiente tabla.
| Operación | Operador en R |
|---|---|
| Valor absoluto | abs() |
| Raíz cuadrada | sqrt() |
| Redondear | round() |
| Techo | ceiling() |
| Piso | floor() |
| Exponencial | exp() |
| Logaritmo | log() |
| Factorial | factorial() |
| Gamma | gamma() |
| Seno | sin() |
| Coseno | cos() |
| Tangente | tan() |
Ayuda sobre funciones
Para obtener información sobre una función concreta o carácter en
R, existen dos métodos que permiten abrir la ventana de ayuda,
el primero es mediante la función help(), la segunda es
mediante el signo ?. Para ilustrar dichos métodos, empleamos la
función if() y el carácter +, para consultar su
ventana de ayuda.
help("if") # Primer método
?"+" # Segundo método
Caso de estudio
Para ilustrar como realizar los diferentes métodos de resúmenes numéricos, tabulares y gráficos, se empleará la siguiente base de datos de EjemploDescriptiva, la cual contiene las siguientes variables
- Municipio: Municipio de residencia de la persona.
- Estrato: Estrato socioeconómico de la vivienda.
- Edad: Edad de la persona en años.
- Altura: Altura de la persona en metros.
- Peso: Peso de la persona en kilogramos.
- Salario: Salario devengado por la persona en pesos.
- SatisTrabajo: Nivel de satisfacción con el trabajo actual.
- DeporFavorito: Deporte favorito de la persona.
Los datos contenidos en la base de datos se presentan a continuación:
| Municipio | Estrato | Edad | Altura | Peso | Salario | SatisTrabajo | DeporFavorito |
|---|---|---|---|---|---|---|---|
| Caldas | 5 | 17 | 1.77 | 66 | 1635100 | Muy satisfecho | Fútbol |
| Bello | 4 | 27 | 1.65 | 90 | 1752500 | Insatisfecho | Fútbol |
| Medellín | 1 | 18 | 1.57 | 66 | 1858400 | Satisfecho | Baloncesto |
| Caldas | 4 | 22 | 1.84 | 87 | 2131400 | Muy satisfecho | Fútbol |
| La Estrella | 3 | 20 | 1.86 | 89 | 1874800 | Satisfecho | Tenis |
| Caldas | 3 | 22 | 1.74 | 90 | 2933100 | Muy satisfecho | Fútbol |
| Itagüí | 1 | 20 | 1.91 | 79 | 1637200 | Muy insatisfecho | Fútbol |
| La Estrella | 3 | 27 | 1.77 | 88 | 1171200 | Indiferente | Baloncesto |
| Itagüí | 2 | 20 | 1.58 | 61 | 2574700 | Muy satisfecho | Baloncesto |
| Bello | 4 | 39 | 1.81 | 70 | 2739000 | Satisfecho | Tenis |
| La Estrella | 6 | 16 | 1.69 | 78 | 2887800 | Indiferente | Baloncesto |
| Bello | 2 | 40 | 1.93 | 83 | 2559600 | Muy satisfecho | Fútbol |
| Medellín | 2 | 26 | 1.93 | 91 | 1906600 | Satisfecho | Fútbol |
| Medellín | 2 | 21 | 1.87 | 61 | 1299700 | Satisfecho | Baloncesto |
| Bello | 4 | 23 | 1.60 | 84 | 1950900 | Indiferente | Fútbol |
| Itagüí | 3 | 40 | 1.91 | 76 | 2131900 | Satisfecho | Fútbol |
| La Estrella | 6 | 31 | 1.79 | 66 | 1085400 | Indiferente | Voleibol |
| La Estrella | 3 | 40 | 1.60 | 67 | 1182200 | Indiferente | Tenis |
| Medellín | 2 | 32 | 1.60 | 88 | 2541900 | Indiferente | Baloncesto |
| Caldas | 3 | 33 | 1.81 | 65 | 1333200 | Muy satisfecho | Fútbol |
Lectura de datos
Para realizar la lectura de datos en R es necesario conocer la extensión que posee el archivo de interés, debido a que R posee diferentes librerías y funciones que permiten la lectura de bases de datos. En la siguiente tabla se resume el origen, la extensión, la librería, y la función para cargar cada base de datos dependiendo de su extensión.
| Origen | Extensión | Librería | Función |
|---|---|---|---|
| Texto | .txt | utils* | read.table() |
| Texto | .csv (comas) | utils* | read.csv() |
| Texto | .csv (punto y coma) | utils* | read.csv2() |
| Excel | .xls | readxl | read_xls() |
| Excel | .xlsx | readxl | read_xlsx() |
| SPSS | .sav | foreign | read.spss() |
| SAS | .sas7bdat | foreign | read.ssd() |
| STATA | .dta | foreign | read.dta() |
Nota: Las librerías con * hacen referencia a funciones integradas en R, y en consecuencia, no es necesario cargarlas antes de usarlas.
Dado que el conjunto de datos empleados en este ejercicio posee un formato .xlsx, se emplea la función read_xlsx() de la librería readxl. En donde se presenta dos métodos de carga. El primero, para realizar la carga desde un fichero local y la segunda, para realizar la carga de datos en linea, en donde se emplea adicionalmente la función tempfile() de base del R y la función download.file() de la librería utils de la base del R.
Carga de datos fichero local
### Instalar y cargar librerías
# install.packages(c('readxl'), dependencies = T) # Instala librería
library(readxl) # Librería para lectura de archivos .xlsx
### Carga archivo
datos <- read_xlsx(file.choose()) # Carga base de datos desde fichero local
Carga de datos en linea
### Instalar y cargar librería
# install.packages('readxl', dependencies = T) # Instala librería
library(readxl) # Librería para lectura de archivos .xlsx
### Crea archivo temporal para cargar archivo online
temp <- tempfile(fileext = ".xlsx")
dataURL <- "https://github.com/jiperezga/jiperezga.github.io/raw/master/Dataset/EjemploDescriptiva.xlsx"
download.file(dataURL, destfile = temp, mode = "wb")
### Carga archivo
datos <- read_xlsx(temp) # Carga la base de datos online
Estructura de datos
El tipo y clase de los datos juega un papel importante al momento de realizar análisis de los datos, debido a que su adecuada especificación será la responsable de que el análisis aplicado a la variable sea el adecuado.
Para observa las clases que poseen los datos, podemos emplear la función str(), de la librería utils de la base del R.
Estructura de los datos
# Muestra la estructura de la base de datos
str(datos)
Classes 'tbl_df', 'tbl' and 'data.frame': 20 obs. of 8 variables:
$ Municipio : chr "Caldas" "Bello" "Medellín" "Caldas" ...
$ Estrato : num 5 4 1 4 3 3 1 3 2 4 ...
$ Edad : num 17 27 18 22 20 22 20 27 20 39 ...
$ Altura : num 1.77 1.65 1.57 1.84 1.86 1.74 1.91 1.77 1.58 1.81 ...
$ Peso : num 66 90 66 87 89 90 79 88 61 70 ...
$ Salario : num 1635100 1752500 1858400 2131400 1874800 ...
$ SatisTrabajo : chr "Muy satisfecho" "Insatisfecho" "Satisfecho" "Muy satisfecho" ...
$ DeporFavorito: chr "Fútbol" "Fútbol" "Baloncesto" "Fútbol" ...
El papel de una correcta estructura de datos, se debe a que podrían haber dentro de la base de datos, variables numéricas tratadas como factores, factores tratadas como numéricas, variables ordinales tratadas como si fueran nominales, etc. Lo cual haría que pueda aplicarse análisis a las variables de forma indebida, por ejemplo, realizar un análisis numérico a una variable que realmente es tipo factor, como es el estrato.
Para convertir una variable de un clase a otra, existen una serie de funciones básicas en la base de R que permiten hacer dicho procedimiento, estas funciones son
- as.numeric(): Convierte una variable a tipo numérico (double).
- as.logical(): Convierte una variable a tipo lógico.
- as.integer(): Convierte una variable a tipo entero.
- as.factor(): Convierte una variable a tipo factor.
- as.character(): Convierte una variable a tipo caracter (character).
- as.ordered(): Convierte una variable a tipo factor asumiendo un orden o jerarquía entre los niveles.
Corrección de estructura de los datos
## Transformar variables a factor
datos$Municipio <- as.factor(datos$Municipio)
datos$DeporFavorito <- as.factor(datos$DeporFavorito)
## Trasforma variable a factor ordinal
datos$Estrato <- as.ordered(datos$Estrato)
datos$SatisTrabajo <- as.ordered(datos$SatisTrabajo)
# En caso de que el orden automático no sea el adecuado
datos$SatisTrabajo <- ordered(datos$SatisTrabajo, c("Muy insatisfecho",
"Insatisfecho","Indiferente", "Satisfecho", "Muy satisfecho"))
# Muestra la estructura de la base de datos
str(datos)
Classes 'tbl_df', 'tbl' and 'data.frame': 20 obs. of 8 variables:
$ Municipio : Factor w/ 5 levels "Bello","Caldas",..: 2 1 5 2 4 2 3 4 3 1 ...
$ Estrato : Ord.factor w/ 6 levels "1"<"2"<"3"<"4"<..: 5 4 1 4 3 3 1 3 2 4 ...
$ Edad : num 17 27 18 22 20 22 20 27 20 39 ...
$ Altura : num 1.77 1.65 1.57 1.84 1.86 1.74 1.91 1.77 1.58 1.81 ...
$ Peso : num 66 90 66 87 89 90 79 88 61 70 ...
$ Salario : num 1635100 1752500 1858400 2131400 1874800 ...
$ SatisTrabajo : Ord.factor w/ 5 levels "Muy insatisfecho"<..: 5 2 4 5 4 5 1 3 5 4 ...
$ DeporFavorito: Factor w/ 4 levels "Baloncesto","Fútbol",..: 2 2 1 2 3 2 2 1 1 3 ...
Resumen numéricos
Una parte importante de la estadística descriptiva, son las medidas estadísticas ya explicadas en la Clase 01 y Clase 02, y aún más importante, es buscar la más adecuada para presentar dichas medidas.
Una alternativa para presentar la información contenida en las medidas estadísticas es mediante resúmenes numéricos, ya que éstos muestran de forma simple y ordenada de forma simultanea conjunto diferentes medidas numéricas, para facilitar su presentación, lectura e interpretación.
Resumen numérico individual
Entre las diferentes funciones que permiten realizar resúmenes numéricos en R, se destaca la función numSummary() de la librería RcmdrMisc y la función describe() de la librería psych, que presentan diferentes medidas estadísticas para variables tipo numéricas.
Resumen numérico con librería RcmdrMisc
### Instalar y cargar librería
# install.packages('RcmdrMisc') # Instala librería RcmdrMisc
library(RcmdrMisc) # Carga librería RcmdrMisc
# Forma básica numSummary
numSummary(datos$Altura)
mean sd IQR 0% 25% 50% 75% 100% n
1.7615 0.1256677 0.225 1.57 1.6375 1.78 1.8625 1.93 20
# Forma avanzada numSummary
numSummary(datos$Altura, statistics = c("mean", "sd", "se", "IQR", "quantiles",
"cv", "skewness", "kurtosis"), type = "3", quantiles = c(0, 0.25, 0.5, 0.75,
1))
mean sd se(mean) IQR cv skewness kurtosis 0%
1.7615 0.1256677 0.02810015 0.225 0.07134129 -0.2094466 -1.49256 1.57
25% 50% 75% 100% n
1.6375 1.78 1.8625 1.93 20
Interpretación
De la salida anterior, se aprecia que la altura promedio de las personas
encuestadas en la base de datos es de \(1.7615\) metros, con una
desviación estándar de \(0.1257\) metros. Adicionalmente de aprecia que
el coeficiente de variación es del \(7.1341\%\) lo cual, dada la
variable evaluada, podría ser considerada como una baja variabilidad en
la altura de todos los encuestados.
También se aprecia que la
Altura mediana de los encuestados es de \(1.78\) metros, lo cual indica
que la altura de los encuestados se encuentran más reunida a la
izquierda, pues se tiene que la mediana posee un valor más alto que la
mediana. Dicho resultado puede ser corroborado al observar el
coeficiente de asimetría, el cual presenta un resultado de \(-0.2094\).
En cuanto al coeficiente de kurtosis, se aprecia que éste
posee un valor de \(-1.4926\), lo cual quiere decir que la distribución
de la altura de los encuestados posee un comportamiento platicúrtico,
esto es, una forma más plana y de colas más pronunciadas.
Finalmente, se aprecia que la altura mínima obtenida en la encuesta es
de \(1.57\) metros, mientras la máxima es de \(1.93\) metros. Dichos
valores se encuentran dentro del rango normal de altura que puede tener
una persona, así que no hay por qué preocuparse por qué estos sean
valores atípicos.
Resumen numérico con librería psych
### Instalar y cargar librería
# install.packages('pysch') # Instala librería pysch
library(psych) # Carga librería pysch
# Forma básica pysch
describe(datos$Altura)
vars n mean sd median trimmed mad min max range skew kurtosis
X1 1 20 1.76 0.13 1.78 1.76 0.16 1.57 1.93 0.36 -0.21 -1.49
se
X1 0.03
# Forma avanzada psych
describe(datos$Altura, ranges = TRUE, trim = 0.1, type = 3, quant = c(0.25,
0.75), IQR = TRUE)
vars n mean sd median trimmed mad min max range skew kurtosis
1 1 20 1.76 0.13 1.78 1.76 0.16 1.57 1.93 0.36 -0.21 -1.49
se IQR Q0.25 Q0.75
1 0.03 0.23 1.64 1.86
Interpretación
Similarmente con esta librería psych, se aprecia que la altura
promedio de las personas encuestadas en la base de datos es de \(1.76\)
metros, con una desviación estándar de \(0.13\) metros, valores que son
iguales a los obtenidos con la librería RcmdrMisc con la
diferencia de que ésta muestra solo dos decimales.
Es de
anotar que al observar la media recortada al \(10\%\) se aprecia que no
hay ningún cambio respecto a su valor promedio sin recortar, lo cual
indica que en los extremos de la distribución no hay posibles valores
influenciales que afecten el cálculo del promedio de las alturas.
También se aprecia que la altura mediana de los encuestados es de
\(1.78\) metros con una desviación absoluta mediana de \(0.16\) metros,
valores similares a los obtenidos en las estadísticas de la media y
desviación estándar, siendo estos último un poco más pequeños.
En cuanto al coeficiente de asimetría y kurtosis, se aprecia que ambos
poseen valores negativos, siendo \(-0.21\) y \(-1.49\), respectivamente,
lo cual indica que el conjunto de alturas encuestadas poseen una
asimetría negativa junto con una forma platicúrtica.
Se
aprecia además, que la diferencia entre el rango de las alturas de la
encuesta posee un valor de \(0.30\) metros, siendo la altura mínima
obtenida en la encuesta de \(1.57\) metros, y la máxima de \(1.93\)
metros. Mientras que el rango intercuartil de las alturas es de \(0.23\)
metros, lo cual es tan solo \(7\) centímetros menos que el rango total
de las observaciones.
Resumen numérico por grupos
También es posible realizar resúmenes numérico por grupos, en donde, para la función numSummary de la librería RcmdrMisc, es cuestión de agregar el argumento groups en donde en este argumento se definirá la variable tipo factor para la cual se desea realizar el agrupamiento. Mientras que con la librería psych es posible realizar resúmenes numéricos por grupos mediante la función describeBy agregando el argumento group, siendo este argumento definido por una variable tipo factor.
Resumen numérico por grupos con librería RcmdrMisc
# Forma avanzada numSummary por grupos
numSummary(data = datos$Peso, groups = datos$DeporFavorito, statistics = c("mean",
"sd", "se", "IQR", "quantiles", "cv", "skewness", "kurtosis"), type = "3",
quantiles = c(0, 0.25, 0.5, 0.75, 1))
mean sd se(mean) IQR cv skewness
Baloncesto 73.66667 12.722683 5.194014 23.25 0.1727061 0.1177989
Fútbol 81.10000 9.550451 3.020118 12.50 0.1177614 -0.5902006
Tenis 75.33333 11.930353 6.887993 11.00 0.1583675 0.3577010
Voleibol 66.00000 NA NA 0.00 NA NaN
kurtosis 0% 25% 50% 75% 100% data:n
Baloncesto -2.111306 61 62.25 72.0 85.50 88 6
Fútbol -1.277242 65 76.75 83.5 89.25 91 10
Tenis -2.333333 67 68.50 70.0 79.50 89 3
Voleibol NaN 66 66.00 66.0 66.00 66 1
Interpretación
De la salida anterior, se aprecia que los cuatro deportes estudiados, se
tiene que los futbolistas poseen un mayor peso en promedio que los otros
deportes, con una media de \(81.1\) kg. También se observa que entre la
información disponible solo hay una persona que practica el Voleibol
cuyo peso es de \(66\) kg.
También se aprecia que el deporte
que posee una mayor desviación estándar es el baloncesto con un total de
\(12\) kg, presentando también el mayor coeficiente de variación con una
variabilidad del \(17%\) respecto a la media.
Entre los
deportes, se aprecia que la distribución del peso de las personas que
juegan baloncesto y tenis poseen distribuciones con asimetría positiva,
mientras que la distribución del peso de las personas que juegan fútbol
posee una distribución con simetría negativa. Respecto a su curtosis, se
tiene que para los tres deportes anteriormente mencionados, se observa
un comportamiento platicúrtico. Es de anotar que el peso de las personas
que juegan voleibol, no posee desviación estándar, asimetría curtosis u
otros estadísticos de variabilidad o forma, debido a que solo se cuenta
con una sola observación.
Resumen numérico por grupos con librería psych
# Forma avanzada pysch por grupos
describeBy(x = datos$Peso, group = datos$DeporFavorito, ranges = TRUE, trim = 0.2,
type = 3, quant = c(0.25, 0.75), IQR = TRUE)
Descriptive statistics by group
group: Baloncesto
vars n mean sd median trimmed mad min max range skew kurtosis se
1 1 6 73.67 12.72 72 73.25 16.31 61 88 27 0.12 -2.11 5.19
IQR Q0.25 Q0.75
1 23.25 62.25 85.5
--------------------------------------------------------
group: Fútbol
vars n mean sd median trimmed mad min max range skew kurtosis se
1 1 10 81.1 9.55 83.5 83.17 9.64 65 91 26 -0.59 -1.28 3.02
IQR Q0.25 Q0.75
1 12.5 76.75 89.25
--------------------------------------------------------
group: Tenis
vars n mean sd median trimmed mad min max range skew kurtosis se
1 1 3 75.33 11.93 70 75.33 4.45 67 89 22 0.36 -2.33 6.89
IQR Q0.25 Q0.75
1 11 68.5 79.5
--------------------------------------------------------
group: Voleibol
vars n mean sd median trimmed mad min max range skew kurtosis se IQR
1 1 1 66 NA 66 66 0 66 66 0 NA NA NA 0
Q0.25 Q0.75
1 66 66
Interpretación
Con la librería psych se observa lo mismo que se mencionó
previamente con la librería RcmdrMisc, en donde los promedios
de peso para los cuatro deportes son, \(73.67\) kg para baloncesto,
\(81.1\) kg para fútbol, \(75.33\) kg para tenis y \(66\) kg para
voleibol. También se aprecia que la media recortada no presenta cambios
significativos respecto a la media con todas las observaciones.
Respecto a las mediana, se observa que para el caso del baloncesto
se tiene un valor menor que su media, con una mediana de \(72\) kg, los
futbolistas un valor mayor que su media con una mediana de \(83.5\) kg y
los tenistas una mediana de \(70\) kg, la cual es \(5\) kg menor a su
media.
También se aprecia que en las medidas de variabilidad,
el deporte que posee una mayor desviación estándar y desviación absoluta
mediana es es el baloncesto con un total de \(12\) kg y \(16.31\) kg,
respectivamente. presentando también el mayor coeficiente de variación
con una variabilidad del \(17%\) respecto a la media.
Finalmente, se evidencia que la distribución del peso de las personas
que juegan baloncesto y tenis poseen asimetrías positivas, mientras que
la distribución del peso de las personas que juegan fútbol una asimetría
negativa. Para la curtosis, se observa que tanto el baloncesto como el
tenis y el fútbol poseen un platicúrtico.
Resumen tabular
Una forma convencional de presentar resúmenes de variables cualitativas, es mediante la construcción de tablas de frecuencias, las cuales permiten presentar de forma individual (una vía) algunas de las características que poseen las variables cualitativas, o de forma conjunta (dos vías) algunas de las características que comparten dichas variables.
Tabla de frecuencias absolutas
Para presentar de forma individual o grupal las características de las variables, puede ser empleada la función table() de la base de R, la cual agrega la información presentada en de las variables de una forma simple, mediante una tabla que presenta el número (frecuencia absoluta) de observaciones que pertenecen a una categoría. Se aconseja que los datos usados dentro de la funcióntable() sean de tipo factor.
Adicionalmente, es posible agregar los totales a las tablas mediante el empleo de la función addmargins de la librería base de R.
Tabla de frecuencias absoluta una vía
# Creación de tabla de frecuencias absolutas en una vía
tabla1via <- table(datos$Municipio)
tabla1via
Bello Caldas Itagüí La Estrella Medellín
4 4 3 5 4
Tabla de frecuencias absoluta una vía con totales
# Agrega las sumas totales a la tabla de frecuencias absolutas en una vía
addmargins(tabla1via)
Bello Caldas Itagüí La Estrella Medellín Sum
4 4 3 5 4 20
Interpretación
En la salida anterior se observa que de la a información disponible, se tiene un total de \(20\) encuestas en donde la mayoría de las personas viven en la Estrella, seguido por un comportamiento similar para las personas que viven en Bello, Caldas y Medellín, en donde se encuentran \(4\) personas encuestadas. Finalmente se tiene que el municipio del cual se tiene menos personas encuestadas es Itagüí con \(3\) personas encuestadas.
Tabla de frecuencias absoluta dos vías
# Creación de tabla de frecuencias absolutas en dos vía
tabla2vias <- table(datos$Municipio, datos$DeporFavorito)
tabla2vias
Baloncesto Fútbol Tenis Voleibol
Bello 0 3 1 0
Caldas 0 4 0 0
Itagüí 1 2 0 0
La Estrella 2 0 2 1
Medellín 3 1 0 0
Tabla de frecuencias absoluta dos vías con totales
# Agrega las sumas totales a la tabla de frecuencias absolutas
# en dos vías, por fila y/o columna
addmargins(tabla2vias, margin = c(1, 2)) # margin = 1 en filas, margin = 2 en columnas
Baloncesto Fútbol Tenis Voleibol Sum
Bello 0 3 1 0 4
Caldas 0 4 0 0 4
Itagüí 1 2 0 0 3
La Estrella 2 0 2 1 5
Medellín 3 1 0 0 4
Sum 6 10 3 1 20
Interpretación
Al observar el cruce entre los municipios y la preferencia por los deportes, observamos que de las \(4\) personas que residen de Bello, hay \(3\) que prefieren practicar fútbol de sobre otros deportes, similar para Caldas e Itagüí, en donde observamos \(4\) y \(2\) personas que prefieren fútbol sobre otros deportes. En La Estrella se aprecia que de los \(4\) encuestados, \(2\) prefieren baloncesto, \(2\) tenis y solo \(1\) voleibol. Mientras que en Medellín, \(3\) de los \(4\) encuestados prefieren baloncesto, y \(1\) fútbol sobre otros deportes.
Tabla de frecuencias relativa
Una alternativa para presentar la información contenida dentro de una variable categórica, es mediante la presentación de tablas de frecuencias relativas, las cuales muestran el valor porcentual al que equivale una categoría específica.
Para la realización de tablas de frecuencias relativas, se emplea la función prop.table(tabla) de base de R, en donde tabla hace referencia a la tabla de frecuencias absolutas creada anteriormente en la subsección anterior.
Tabla de frecuencias relativas una vía
# Creación de tablas de frecuencias relativas en una vía
prop1via <- prop.table(tabla1via)
prop1via
Bello Caldas Itagüí La Estrella Medellín
0.20 0.20 0.15 0.25 0.20
Tabla de frecuencias absoluta una vía con totales
# Agrega las sumas totales a la tabla de frecuencias relativas en una vía
addmargins(prop1via)
Bello Caldas Itagüí La Estrella Medellín Sum
0.20 0.20 0.15 0.25 0.20 1.00
Interpretación
En la tabla de la salida anterior se presenta la proporción de encuestas realizadas en cada municipio, en donde en los municipios de Bello, Caldas y Medellín se realizó en cada una un \(20\%\) de las encuestas, mientras que en la Estrella e Itagüí se realizó un \(25\%\) y \(15\%\) de las encuestas respectivamente.
Tabla de frecuencias relativas dos vías
# Creación de tabla de frecuencias relativas en dos vías
prop2vias <- prop.table(tabla2vias)
prop2vias
Baloncesto Fútbol Tenis Voleibol
Bello 0.00 0.15 0.05 0.00
Caldas 0.00 0.20 0.00 0.00
Itagüí 0.05 0.10 0.00 0.00
La Estrella 0.10 0.00 0.10 0.05
Medellín 0.15 0.05 0.00 0.00
Tabla de frecuencias relativas dos vías con totales
# Agrega las sumas totales a la tabla de frecuencias relativas en dos vías
# por fila y/o columna
addmargins(prop2vias, margin = c(1, 2))
Baloncesto Fútbol Tenis Voleibol Sum
Bello 0.00 0.15 0.05 0.00 0.20
Caldas 0.00 0.20 0.00 0.00 0.20
Itagüí 0.05 0.10 0.00 0.00 0.15
La Estrella 0.10 0.00 0.10 0.05 0.25
Medellín 0.15 0.05 0.00 0.00 0.20
Sum 0.30 0.50 0.15 0.05 1.00
Interpretación
En la salida anterior, se presentan la proporción de personas encuestadas a partir del municipio y su deporte favorito, en donde se aprecia que las combinaciones Bello-Fútbol y Medellín-Baloncesto poseen el \(15\%\) del total de las encuestas, Caldas-Fútbol el \(20\%\), Itagüí-Fútbol, La Estrella-Baloncesto y La Estrella-Tenis el \(10\%\), y Bello-Tenis, Itagüí-Baloncesto y Medellín Fútbol \(5\%\). Es de anotar que entre los municipios con mayor porcentaje se tiene a La estrella con \(25\%\) y el deporte preferido sobre los demás el \(50\%\).