Inferencia estadística
La inferencia estadística es la obtención de conclusiones basadas en datos experimentales. Para entender la naturaleza de la inferencia estadística, se debe entender primero la diferencia entre “población” y “muestra.”
Población: Consta del total de observaciones del suceso o proceso en que estamos interesados. En muchas ocasiones, no es posible obtener o replicar dicha información.
Muestra: Es un subconjunto de la población de interés, extraída con el objetivo de hacer inferencia sobre la población.
Muestra aleatoria: Es un subconjunto de la población seleccionado de forma independiente e idénticamente distribuidos (iid en adelante).
Estadísticos
Son funciones de las variables aleatorias obtenidas a partir de muestras aleatorias, que tienen por objetivo estimar o hacer inferencia acerca de parámetros desconocidos de una población.
A continuación se definirán algunos estadísticos importantes que sirven para medir el centro y la dispersión de un conjunto de datos, acomodados por orden de magnitud.
Estadísticos muestrales
Sea $X_1, X_2, \ldots, Xn$ una muestra aleatoria iid de tamaño
$n$, entonces se tendrán los siguientes estadísticos muestrales
Media muestral
Es el promedio aritmético del total de las $n$ observaciones
pertenecientes a una muestra aleatoria. Éste estadístico se define como
\begin{align*} \bar{X}=\sum_{i=1}^n\frac{x_i}{n}=\frac{x_1+x_2+\ldots+x_n}{n} \end{align*}
En Excel, puede calcularse el valor promedio de un conjunto de
observaciones mediante la función PROMEDIO().
Varianza muestral
Es la distancia media al cuadrado del conjunto de observaciones
pertenecientes a una muestra aleatoria, respecto a la media muestra.
\begin{align*} S^2=\frac{1}{n-1}\sum_{i=1}^n{(x_i-\bar{X})^2} \end{align*}
siendo el valor $n-1$ conocido como la corrección de Bessel, el cuál
se usa en lugar de la división sobre $n$ con el fin de corregir el
sesgo tendría el estimador.
En Excel puede calcularse la varianza de un conjunto de observaciones
mediante la función VAR.S().
Desviación estándar muestral
Es la raíz cuadrada de la distancia media al cuadrado del conjunto
de observaciones pertenecientes a una muestra aleatoria, respeto a la
media, es decir, indica qué tan dispersos se encuentra el conjunto de
observaciones de una muestra aleatoria respecto a su valor promedio.
\begin{align*} S=\sqrt{S^2} \end{align*}
En Excel puede calcularse la desviación estándar de un conjunto de
observaciones mediante la función DESVEST.M().
Proporción muestral
Representa la proporción de observaciones que cumplen cierta
característica dentro de una muestra aleatoria, indica qué porcentaje de
la muestra pertenece a la categoría de interés, y por tanto, puede ser
calculada mediante la definición de frecuencia relativa, tal que
\begin{align*} \hat{p}=\frac{x}{n} \end{align*} siendo $x$ el
número de éxitos en la muestra, y $n$ el total de observaciones de la
muestra aleatoria.
Prueba de hipótesis
Una hipótesis estadística es una afirmación o conjetura que se realiza sobre una población o sobre los parámetros de la misma, en donde el objetivo es decidir si la afirmación hecha se encuentra apoyada por la información obtenida de una muestra de la población de interés.
Por ejemplo, un médico afirma que el peso ideal de las personas de
cierta población sigue una distribución normal con peso promedio de
$73$kg y desviación estándar de $3$kg.
Componentes de una prueba de hipótesis
Hipótesis nula
Sea $\theta$ un parámetro de interés desconocido y sea $\theta_0$ un
valor particular de $\theta$, entonces se tendrá que la hipótesis nula
estará dado por
- Bilateral
$H_0: \theta = \theta_0$ - Unilateral izquierda
$H_0: \theta \geq \theta_0$ - Unilateral derecho
$H_0: \theta \leq \theta_0$
matemáticamente $H_0: \theta \geq \theta_0$ y
$H_0: \theta \leq \theta_0$ es matemáticamente equivalente a escribir
$H_0: \theta = \theta_0$ y por tanto, se acostumbra a usar esta última
en los tres casos.
Hipótesis alternativa
Es el complemento lógico de la hipótesis nula, y por tanto, ésta estará dado por
- Bilateral
$H_1: \theta \neq \theta_0$ - Unilateral izquierda
$H_1: \theta < \theta_0$ - Unilateral derecho
$H_1: \theta > \theta_0$
Ésta hipótesis no puede contener la igualdad, a menos que se quiera una hipótesis alternativa específica.
Estadístico de prueba
El estadístico de prueba será el valor usado para tomar la decisión
entre $H_0$ y $H_1$. Éste dependerá del parámetro de interés y de la
distribución muestral del estadístico. Entre los estadísticos de prueba
más usados de tiene a $Z$, $t_v$. $\chi^2_v$ y $F_{v_1,v_2}$.
Región crítica
La región crítica o región de rechazo representa los valores del
estadístico de prueba que conduce a rechazar la hipótesis nula, es
decir,
\begin{align*} RC:\{\text{valores del estadístico de prueba que conducen a rechazar }H_0\} \end{align*}
Por ejemplo, si se emplea la afirmación del médico sobre el peso
promedio de los estudiantes, se tendrá el siguiente juego de hipótesis
\begin{align*} H_0: \mu = 73 kg \\ H_1: \mu \neq 73 kg \end{align*}
Supongamos una región crítica arbitraria, tal que
\begin{align*} RC:\{\bar{X}|\bar{X}<71 \text{ o } \bar{X}>75\} \end{align*}
P-valor
Es el nivel de significancia más bajo en el que el valor observado del
estadístico de prueba es significativo. Por tanto, un valor
relativamente pequeño puede sugerir que el valor observado del
estadístico de prueba sea poco probable, y por tanto, $H_0$ deba ser
rechazado.
Dado que el P-valor puede interpretarse como el tamaño de la región
crítica $RC$ que se obtiene a partir de los datos, entonces para un
nivel de significancia preestablecido, el criterio de decisión debe ser
\begin{align*} \text{P-valor }<\alpha \Rightarrow \text{ Rechazar } H_0 \end{align*}
Prueba de bondad de ajuste
Las pruebas de bondad de ajuste son un contraste de hipótesis para determinar el grado o nivel de ajuste de nuestros datos a una distribución teórica.
Estas pruebas se basan en la comparación de las frecuencias de ocurrencia observadas en una muestra empírica y las frecuencias esperadas de una distribución teórica. En donde, el objetivo será si existe o no discrepancia entre los valores observados y los valores esperados de la distribución de interés.
La hipótesis a probar de interés estará dada por
\begin{align*} H_0: X \sim F_0(x) \quad \text{vs} \quad H_1: X \nsim F_0(x) \end{align*}
Siendo $F_0(x)$ la distribución de probabilidad hipotética que se
quiere probar.
Entre las pruebas de bondad de ajuste más usadas se tiene:
- Prueba Kolmogorov–Smirnov
- Prueba Cramér–von Mises
- Prueba Anderson–Darling
- Prueba Chi-Cuadrado
- Prueba Kuiper
Además, en el caso de probas específicas para detectar normalidad se tiene
- Prueba Shapiro-Wilk
- Prueba Lilliefors
- Prueba Shapiro-Francia
Es de anotar que a pesar de que este conjunto de pruebas suelen ser las más usadas, en el software Excel, no se encuentra implementada ninguna de ellas, y su programación suele ser complicada.
Por ello se recomienda en Excel calcular la prueba Jarque-Bera para probar si los datos se distribuyen o no de forma aproximadamente normal, tal que el juego de hipótesis a probar será
\begin{align*} H_0&: \text{El conjunto de datos tiene una distribución aproximadamente normal} \\ H_1&: \text{El conjunto de datos NO tiene una distribución aproximadamente normal} \end{align*}
en donde el estadístico de prueba estará dado por
\begin{align*} JB = \frac{n}{6} \left[\gamma_1^2 + \left(\frac{\gamma_2^2}{4}\right)\right] \sim \chi^2_2 \end{align*}
donde $n$: representa el número total de datos, $\gamma_1$:
representa el coeficiente de asimetría que posean los datos, y
$\gamma_2$: representa el coeficiente de exceso de curtosis.
Finalmente, para decidir si se rechaza o no la hipótesis nula sobre la
normalidad de los datos se puede emplear como criterio de decisión el
P-valor, mediante una distribución Chi-Cuadrado con dos grados de
libertad, tal que
\begin{align*} \text{P-Valor} = \mathbb{P}(\chi^2_2 > JB) \end{align*}
Una alternativa final para observar si los datos se distribuyen como una distribución específica son los gráficos Cuartil-Cuartil, los cuales se construyen al comparar los cuartiles del conjunto de datos observados, contra los cuartiles de la distribución de interés.
Prueba de hipótesis para la media $\mu$
Sea $X_1, X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$ con media desconocida $\mathbb{E}(X)=\mu$, y varianza
$Var(X)=\sigma^2<\infty$, entonces dependiendo de las condiciones, se
tendrán los siguientes pruebas de hipótesis para la media $\mu$.
Ejercicio
Suponga que se realiza un estudio sobre los costos que han tenido proyectos de renovación de parques en la ciudad de Medellín, encontrando que los costos asociados a \(20\) proyectos que se han a cabo en le ciudad, en millones de pesos, fueron de
| 1780 | 2933 | 1220 | 1278 | 1170 | 1032 | 1245 | 2070 | 2040 | 1289 |
| 1531 | 980 | 1730 | 1380 | 2243 | 1687 | 1422 | 1731 | 1435 | 2080 |
Si es posible supone que el costo de construir cualquier parque se distribuyen aproximadamente normal, pruebe si el costo promedio máximo que tiene la construcción de un nuevo parque es de \(2000\) millones de pesos. Emplee un nivel de significancia del \(2\%\).
Solución
En este caso estamos interesados en probar si el costo promedio de
construir un nuevo parque sea máximo de \(2000\) millones de pesos, y
por tanto se tendrá que el juego de hipótesis estará dado por
\[\begin{align*}
H_0: \mu \leq 2000 \\
H_1: \mu > 2000
\end{align*}\]
para decidir el estadístico de prueba que debemos emplear, se debe
revisar la información que poseemos, en donde tenemos que la varianza
poblacional no es conocida, ya que no la mencionan en el enunciado,
además nos mencionan que los costos se distribuyen aproximadamente
normal. Entonces, al ser el tamaño muestral pequeño e igual a \(20\)
datos, las características del ejercicio están dados por
de lo anterior encontramos que el intervalo de confianza de interés es
de la forma \[\begin{align*}
t_c = \frac{\bar{X} - \mu_0}{S/\sqrt{n}} \sim t_{n-1}
\end{align*}\]
En donde observamos que requerimos del valor de la media muestral
\(\bar{X}=1613.8\), el valor asociado a la hipótesis nula
\(\mu_0=2000\), la desviación estándar muestral \(S=480.1471\) y el
tamaño de muestra \(n=20\). Al reemplazar en el estadístico de prueba se
tendrá que \[\begin{align*}
t_c &= \frac{1613.8 - 2000}{480.1471/\sqrt{20}}\\
&= -3.597104
\end{align*}\]
Ahora, para saber si se rechaza o no la hipótesis nula, se realiza el
cálculo de la región crítica, obteniendo que \[\begin{align*}
RC:\{t|t>t_{\alpha, n-1}\}
\end{align*}\]
en donde, al usar el valor \(\alpha=0.02\) y \(n=20\), se tendrá que la
región crítica al emplear la función de Excel
INV.T(1-\(\alpha\), n-1) será igual a \[\begin{align*}
RC&:\{t|t>t_{\alpha=0.02, n-1=19}\}\\
RC&:\{t|t>2.204701\}
\end{align*}\]
Entonces como el valor crítico no cae dentro de la región crítica, no se
rechaza la hipótesis nula, y por tanto se concluye con un nivel de
significancia del \(2\%\) que el costo promedio máximo que costará
construir un nuevo parque no será mayor a \(2000\) millones de pesos.
Ejercicio
Suponga que Postobon desarrolla una nueva máquina de bebidas para servir
de forma automática gaseosas en los cines, de tal forma que la cantidad
servida, en mililitros, se distribuye Weibull con varianza de
\(5703.473_{ml^2}\). Si la máquina sirve en promedio menos de
\(330_{ml}\) por vaso, Postobon decidirá no sacar al mercado la máquina
debido a que no cumple con los estándares establecidos.
Para
probar si las máquinas funcionan bien, se decide tomar una muestra
aleatoria de \(5000\) vasos de gaseosa servidos por las nuevas máquinas
de bebidas, obteniendo una promedio de \(327_{ml}\), con una varianza de
\(5240.35_{ml^2}\). Basados en lo anterior, prueba con un nivel de
significancia del \(5\%\) si la nueva máquina cumple con los estándares
establecidos.
Solución
En este caso estamos interesados en probar la hipótesis de que la
cantidad servida por la nueva máquina no es menor a \(330_{ml}\) por
vaso, empleando un nivel de significancia del \(5\%\), y por tanto,
tendremos que el juego de hipótesis estará dado por \[\begin{align*}
H_0:\mu \leq 330\\
H_1:\mu < 330
\end{align*}\]
Entonces dado que estamos en una situación en la cual sabemos que la
población no es normal, debido a que se menciona que es Weibull, con
varianza conocida e igual a \(5703.473_{ml^2}\), estaremos bajo la
siguiente situación
de lo anterior encontramos que el estadístico de prueba de interés es de
la forma \[\begin{align*}
Z_c = \frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} \sim N(0,1)
\end{align*}\]
En donde observamos que requerimos la media muestral \(\bar{X}=327\), la
desviación estándar poblacional \(\sigma=75.52134\), el tamaño de
muestra \(n=5000\), el nivel de significancia \(\alpha=0.05\) y el valor
crítico \(-Z_{\alpha=0.05}=-1.644854\) calculado mediante la función
INV.NORM.ESTAND(1-\(\alpha\)). Al reemplazar en el
estadístico de prueba tenemos que \[\begin{align*}
Z_c &= \frac{327-330}{75.52134/\sqrt{5000}} \\
&= -2.808902
\end{align*}\]
En esta ocasión se decide calcular el P-valor para tomar la decisión, el
cual al emplear la función DISTR.NORM.ESTAND.N(-2.808902;
VERDADERO) se tendrá que \[\begin{align*}
P-valor &= \mathbb{P}(Z<Z_c)\\
&= \mathbb{P}(Z<-2.808902)\\
&= 0.002485539
\end{align*}\]
Entonces, como el P-valor es menor al nivel de significancia
\(\alpha=0.05\), se tendrá evidencia suficiente para rechazar la
hipótesis nula, y por tanto se concluirá con un nivel de significancia
del \(5\%\) que la cantidad promedio de llenado de las gaseosas por vaso
es menor a \(330_{ml}\), lo cual significa que Postobon debería sacar la
máquina del mercado para recalibrarla.
Ejercicio
Suponga que la marca de cigarrillo Malboro es auditada debido a que se
afirma que sus registros están adulterados. Ante ésto, el presidente de
la empresa asegura que sus registros son correctos y que el flujo de
caja promedio mensual que registran es de \(25\) mil millones de pesos.
Para probar si dicha afirmación es posible, el auditor decide revisar el
flujo de caja de la empresa de los últimos \(48\) meses, encontrando que
el flujo de caja promedio que registra la empresa es de \(21.389\) mil
millones de pesos con una desviación estándar de \(3.213\) mil millones
de pesos.
Si puede suponerse que el flujo de caja de la
empresa Malboro se distribuye normalmente, emplee un nivel de confianza
del \(10\%\) para probar si la afirmación del presidente se encuentra
respaldada por la información muestral.
Solución
En este ejercicio se está interesado en probar la hipótesis sobre que el
flujo de caja promedio mensual es igual a \(25\) mil millones de pesos,
lo cual significa que al posee la igualdad la afirmación, tendremos el
siguiente juego de hipótesis \[\begin{align*}
H_0:\mu = 25\\
H_1:\mu \neq 25
\end{align*}\]
Entonces para saber cual es el estadístico de prueba que debemos
aplicar, debemos inicialmente verificar qué información poseemos. De la
información suministrada tenemos que el flujo de caja de la empresa se
distribuye normalmente con una varianza desconocida, y por tanto
estaremos ante la siguiente situación
lo cual quiere decir que el estadístico de prueba estará dado por
\[\begin{align*}
Z_c = \frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} \stackrel{a}{\sim} N(0,1)
\end{align*}\]
En donde observamos que necesitamos la media muestral
\(\bar{X}=21.389\), la desviación estándar muestral \(S=3.213\), el
tamaño de muestra \(n=48\) y el nivel de significancia \(\alpha=0.10\).
Al reemplazar estos valores tendremos que \[\begin{align*}
Z_c &= \frac{21.389-25}{3.213/\sqrt{48}}\\
&= -7.786412
\end{align*}\]
Entonces si empleamos la región crítica para la toma de decisión,
tendremos que \[\begin{align*}
RC:\{Z|Z<-Z_{\frac{\alpha}{2}} \text{ ó } Z>Z_{\frac{\alpha}{2}}\}
\end{align*}\]
en donde al emplear la función de Excel
INV.NORM.ESTAND(1-\(\alpha\)) encontraríamos que el valor
crítico \(Z_{\frac{\alpha}{2}=0.05}=1.644854\) y por tanto la región
crítica será \[\begin{align*}
RC:\{Z|Z<-1.644854 \text{ ó } Z>1.644854\}
\end{align*}\]
En donde al comparar el estadístico de prueba con la región crítica,
encontramos que el estadístico de prueba cae dentro de la región
crítica, y por tanto hay evidencia suficiente para rechazar la hipótesis
nula, lo cual quiere decir con un nivel de significancia del \(10\%\)
que el flujo de caja promedio mensual que registra la marca de
cigarrillos Malboro es diferente a \(25\) mil millones de pesos.
Prueba de hipótesis para diferencia de medias $\mu_1 - \mu_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias iid de
tamaños $n_1$, y $n_2$ con medias desconocidas
$\mathbb{E}(X_{1})=\mu_1$ y $\mathbb{E}(X_{2})=\mu_2$, y varianzas
$Var(X_{1})=\sigma_1^2<\infty$ y $Var(X_{2})=\sigma^2_2<\infty$,
respectivamente, entonces dependiendo de las condiciones, se tendrán los
siguientes pruebas de hipótesis para la diferencia de medias
$\mu_1 - \mu_2$.
Ejercicio
Una empresa de electrodomésticos desea saber si los cursos de
capacitación sirven para mejorar el nivel de ventas de sus trabajadoras
y para ello decide enviar a \(12\) de sus agentes de ventas a dicho
curso. Una vez finalizado el curso, la empresa encuentra que estos
agentes generan unas ventas promedio de de \(43.5\) millones de pesos
con una desviación estándar de \(3.1\) millones de pesos.
Con
el fin de observar si el curso es o no efectivo, la empresa extrae una
muestra aleatoria independiente de \(15\) agentes que no asistieron a la
capacitación y encontró que las ventas promedio generadas y su
desviación estándar para estos agentes fue de \(40.8\) y \(2.3\)
millones de pesos respectivamente.
Si es posible suponer que
las poblaciones se distribuyen normalmente con varianzas iguales a
\(5.6\) millones de pesos\(^2\) para quienes se capacitaron y a \(4.3\)
millones de pesos\(^2\) para quienes no se capacitaron, emplee un nivel
de significancia del \(5\%\) para observar si es posible pensar que los
cursos de capacitación mejoran el promedio de ventas sobre quienes no
recibieron estos cursos?.
Solución
En este ejercicio estamos interesados en emplear un nivel de
significancia del \(5\%\) para probar la hipótesis de que las ventas de
las personas que tomaron los cursos de capacitación son superiores a las
ventas de quienes no tomaron los cursos de capacitación, la cual es de
la forma \[\begin{align*}
H_0:\mu_C \leq \mu_S => \mu_C - \mu_S \leq 0\\
H_1:\mu_C > \mu_S => \mu_C - \mu_S > 0\\
\end{align*}\]
donde el subíndice \(C\) representa “con capacitación” y el subíndice
\(S\) representa “sin capacitación.” Ahora, para decidir si cual es el
estadístico de prueba adecuado, se verifica la información que poseemos,
en donde nos mencionan que las poblaciones se distribuyen normalmente
con varianzas conocidas e iguales a \(\sigma^2_C=5.6\) y
\(\sigma^2_S=4.3\) millones de pesos\(^2\). Lo cual nos llevará a la
siguiente situación
encontrando que el estadístico de prueba de interés es de la forma
\[\begin{align*}
Z_c = \frac{(\bar{X}_C-\bar{X}_S) - d_0}{\sqrt{\frac{\sigma^2_C}{n_C}+\frac{\sigma^2_S}{n_S}}} \sim N(0,1)
\end{align*}\]
En donde, para realizar el cálculo requerimos de las media muestrales
fueron \(\bar{X}_C=43.5\) y \(\bar{X}_S=40.8\), las varianzas
poblacionales \(\sigma^2_C=5.6\) y \(\sigma^2_S=4.3\), los tamaños de
muestrales \(n_C=12\) y \(n_S=15\). Al reemplazar en la ecuación del
estadístico de prueba tendremos que \[\begin{align*}
Z_c &= \frac{(43.5-40.8) - 0}{\sqrt{\frac{5.6}{12}+\frac{4.3}{15}}}\\
&= 3.110786
\end{align*}\]
Ahora, para tomar una decisión suponga que se decide emplear el P-valor,
el cual al ser una hipótesis bilateral, tendremos que está dado por
\[\begin{align*}
P-valor &= \mathbb{P}(Z > Z_c) \\
&= \mathbb{P}(Z > 3.110786) \\
&= \mathbb{P}(Z > 3.110786)
\end{align*}\]
Entonces al emplear la función de Excel 1 -
DISTR.NORM.ESTAND.N(3.110786; VERDADERO) tendremos que el P-valor
es igual a \[\begin{align*}
P-valor &= \mathbb{P}(Z > 3.110786) \\
&= 0.000932951 \\
\end{align*}\]
Entonces como el P-valor es menor al nivel de significancia del \(5\%\)
se rechazará la hipótesis nula, y por tanto se tendrá evidencia
suficiente para concluir que el promedio de ventas de las personas que
recibieron capacitación es superior al promedio de ventas de las
personas que no recibieron capacitación.
Ejercicio
La gobernación de Antioquia, desea construir un nuevo puente para
comunicar el municipio de Itagüí con Envigado, y para ello tiene dos
posibles ubicaciones en los cuales puede llevar a cabo dicho proyecto.
Para decidir en cual de las dos ubicaciones llevar a cabo el proyecto
decide tomar muestras aleatorias de cada ubicación y mirar en cual de
los dos hay mayor aflucencia de vehículos.
De la ubicación
\(A\) se decide tomar una muestra aleatoria de \(22\) días y de la
ubicación \(B\) de \(28\) días encontrando respectivamente que el número
promedio de vehículos para cada ubicación fue de \(2359\) y \(2147\)
vehículos, con una desviación estándar de \(143\) y \(301\) vehículos.
Si puede asumirse que el número de vehículos en las dos zonas
se distribuye aproximadamente normal con varianzas iguales, pruebe con
un nivel de significancia del \(10\%\) si la afluencia de vehículos que
transitan por la ubicación \(A\) es menor que la afluencia de vehículos
que transitan por la ubicación \(B\).
Solución
En este punto estamos interesados en una hipótesis unilateral, debido a
que queremos probar si el número de vehículos que transitan por día por
la ubicación \(A\) es menor que la ubicación \(B\), lo cual puede
traducirse bajo el juego de hipótesis \[\begin{align*}
H_0:\mu_A \geq \mu_B => \mu_A - \mu_B \geq 0\\
H_1:\mu_A < \mu_B => \mu_A - \mu_B < 0\\
\end{align*}\]
En donde al revisar la información suministrada se encontró que el
número de vehículos en las dos zonas se distribuyen aproximadamente
normal con varianzas iguales pero desconocidas y tamaños muestrales
pequeñas, por lo cual nos encontraremos en la siguiente situación
en donde se aprecia que el estadístico de prueba estará dado por
\[\begin{align*}
t_c = \frac{(\bar{X}_A-\bar{X}_B) - d_0}{S_p\sqrt{\frac{1}{n_A}+\frac{1}{n_B}}} \sim t_{n_A + n_B - 2}
\end{align*}\]
En donde se observa que para realizar el cálculo requerimos de los
tamaños muestrales \(n_A=22\) y \(n_B=28\), las medias muestrales
\(\bar{X}_A=2359\) y \(\bar{X}_B=2147\), y una desviación estándar
conjunta \(S_p\), la cual no poseemos, y que debemos calcular, pero que
podemos obtener mediante la ecuación \[\begin{align*}
Sp^2 &= \frac{(n_A-1)S^2_A + (n_B-1)S^2_B}{n_A+n_B-2} \\
&= \frac{(22-1)143^2 + (28-1)301^2}{22 + 28 - 2} \\
&= 59909.5
\end{align*}\] y por tanto \[\begin{align*}
Sp &= \sqrt{Sp^2} \\
&= \sqrt{59909.5} \\
&= 244.7642
\end{align*}\]
Una vez conocidos los valores necesarios para calcular el estadístico de
prueba, tendremos que \[\begin{align*}
t_c &= \frac{(2359-2147) - 0}{244.7642\sqrt{\frac{1}{22}+\frac{1}{28}}} \\
&= 21.49702
\end{align*}\]
Ahora, si empleamos P-valor para tomar una decisión, tendremos que
\[\begin{align*}
P-valor &= \mathbb{P}(t_{n_A+n_B-2}<t_c) \\
&= \mathbb{P}(t_{22+28-2}<21.49702) \\
&= \mathbb{P}(t_{48}<21.49702)
\end{align*}\]
En donde al realizar el cálculo en Excel mediante la función
DISTR.T.N(21.49702;48;VERDADERO), tendremos que
\[\begin{align*}
P-valor &= \mathbb{P}(t_{48}<21.49702) \\
&= 1
\end{align*}\]
y por tanto, como el P-valor es superior al nivel de significancia del
\(10\%\), no se rechaza al hipótesis nula y se tendrá que hay evidencia
suficiente para concluir que el número de vehículos que transitan por la
ubicación \(A\) no es menor a la ubicación \(B\).
Ejercicio
Suponga que la Universidad de Antioquia adelanta un estudio sobre el
salario de sus egresados y desea comparar si es cierta la creencia que
las mujeres ganan en promedio menos dinero que los hombres.
Para comprobar si las creencias son ciertas, un grupo de investigación
de la Universidad toma una muestra representativa de \(250\) mujeres y
\(270\) hombres egresados de la Universidad y se les pregunta sobre cuál
es el salario que ganan actualmente, obteniendo en su investigación que
las mujeres ganan en promedio \(2.3\) millones de pesos con una
desviación estándar de \(0.7\) millones de pesos, mientras que los
hombres ganan en promedio \(2.6\) millones de pesos con una desviación
estándar de \(1.2\) millones de pesos.
Si el grupo de
investigación encuentra que los salarios no se distribuyen normalmente,
emplee un nivel de significancia del \(15\%\) para probar si el salario
de los egresados hombres es mayor al salario de los egresados mujeres.
Solución
En este enunciado estamos interesados en probar con un nivel de
significancia del \(15\%\) si el salario de los hombres es mayor al de
las mujeres, lo cual se traduce en el siguiente juego de hipótesis
\[\begin{align*}
H_0:\mu_H \leq \mu_M => \mu_H - \mu_M \leq 0\\
H_1:\mu_H > \mu_M => \mu_H - \mu_M > 0\\
\end{align*}\]
entonces para probar si la hipótesis es o no apoyada por la información
muestral, es necesario realizar el cálculo de una estadístico de prueba,
y para ello se revisa la información que poseemos, en donde al tener que
los salarios no se distribuyen normalmente con varianzas desconocidas
(debido a que no nos mencionan nada de ellas) pero con muestras grandes,
obteniendo la siguiente situación
En donde se observa que el estadístico de prueba está dado por
\[\begin{align*}
Z_c = \frac{(\bar{X}_H-\bar{X}_M) - d_0}{\sqrt{\frac{S^2_H}{n_H}+\frac{S^2_M}{n_M}}} \stackrel{a}{\sim} N(0,1)
\end{align*}\]
En donde observamos que para realizar el cálculo se requiere de los
tamaños muestrales \(n_M = 250\) y \(n_H = 270\), las medias muestrales
\(\bar{X}_M=2.3\) y \(\bar{X}_H=2.6\), con desviaciones estándar
muestrales iguales a \(S_M=0.7\) y \(S_H=1.2\). Por tanto al reemplazar
los valores en el estadístico de prueba se tendrá que \[\begin{align*}
Z_c &= \frac{(2.6-2.3) - 0}{\sqrt{\frac{1.2}{270}+\frac{0.7}{250}}} \\
&= 3.524672
\end{align*}\]
Ahora, si empleamos la región crítica para observar si se rechaza o no
la hipótesis, tendremos que al emplear la función de Excel
INV.NORM.ESTAND(1-\(\alpha\)), se tendrá que
\[\begin{align*}
RC&:\{Z|Z>Z_\alpha\}\\
RC&:\{Z|Z>1.03643\}
\end{align*}\]
Entonces como el estadístico de prueba cae dentro de la región crítica,
se tendrá evidencia suficiente para rechazar la hipótesis nula, lo cual
significa con un nivel de significancia del \(15\%\) que el salario
promedio de los hombres es mayor al salario promedio de las mujeres.
Ejercicio
Se realiza un estudio con el fin de comparar el rendimiento de
combustible en kilómetros por galón para dos tipos de motores \(A\) y
\(B\). Suponga que se decide realizar un total de \(47\) experimentos
con el motor \(A\) y \(56\) experimentos con el motor \(B\), encontrando
para cada caso, un rendimiento promedio de gasolina de \(44\) y \(48\)
kilómetros, respectivamente, con desviaciones estándar de \(8.3\) y
\(6.6\), respectivamente.
Basados en la información anterior,
pruebe con un nivel de significancia del \(12\%\) si la diferencia
promedio entre los rendimientos de combustible en kilómetros por galón
de gasolina para los motores \(A\) y \(B\) son o no iguales, si es
posible suponer que los rendimientos de los combustibles no poseen una
distribución normal y poseen varianzas conocidas e iguales a \(38.44\) y
\(57.76\) para los motores \(A\) y \(B\) respectivamente.
Solución
En este caso estamos interesados en calcular con un nivel de
significancia del \(12\%\) si la diferencia entre los rendimientos
promedios de combustible son o no iguales, es decir, se quiere probar el
juego de hipótesis \[\begin{align*}
H_0:\mu_A - \mu_B = 0\\
H_1:\mu_A - \mu_B \neq 0\\
\end{align*}\]
Entonces dado que los rendimientos de combustible para los dos motores
se distribuye normalmente con varianzas conocidas, estaremos en la
siguiente situación
En donde se aprecia que el estadístico de prueba está dada por
\[\begin{align*}
Z_c = \frac{(\bar{X}_A-\bar{X}_B) - d_0}{\sqrt{\frac{\sigma^2_A}{n_A}+\frac{\sigma^2_B}{n_B}}} \sim N(0,1)
\end{align*}\]
observando que se requiere de los rendimientos promedio muestrales de
los dos motores \(\bar{X}_A=44\) y \(\bar{X}_B=48\), las varianzas
poblacionales \(\sigma^2_A=38.44\) y \(\sigma^2_B=57.76\) y los tamaños
muestrales \(n_A=47\) y \(n_B=56\). Al reemplazar estos valores en el
estadístico de prueba se tendrá que \[\begin{align*}
Z_c &= \frac{(44-48) - 0}{\sqrt{\frac{38.44}{47}+\frac{57.76}{56}}} \\
&= -2.941414
\end{align*}\]
Ahora, si realizamos el cálculo de la región crítica para observar si se
rechaza o no la hipótesis establecida, tendremos que al emplear la
función de Excel
INV.NORM.ESTAND(1-(\(\alpha\)/2)), se tendrá que
\[\begin{align*}
RC&:\{Z|z < -Z_{\alpha/2} \text{ ó } Z>Z_{\alpha/2}\}\\
RC&:\{Z|Z<-1.5548 \text{ ó } Z>1.55478\}
\end{align*}\]
apreciando que el estadístico de prueba cae dentro de la región crítica
lo cual significa que con un nivel de significancia del \(12\%\) se
rechaza la hipótesis nula, de que el rendimiento promedios de
combustible de los dos tipos de motores son iguales, y por tanto se
tendrá que hay diferencias significativas entre el rendimiento promedio
de combustible de los motores.
Ejercicio
Suponga que se contrata a un grupo de investigación de la Universidad de
Antioquia para que realice un análisis de tensión sobre la unión pegada
con una resina experimental a dos clases diferentes de madera. Para
realizar el estudio, el grupo de investigación toma una muestra
aleatoria de \(18\) uniones pegadas con la resina especial a la madera
\(A\) y encontró que la tensión promedio de corte y desviación estándar
fueron de \(1130_{psi}\) y \(420_{psi}\), respectivamente. Por su parte,
toman una muestra aleatoria de \(12\) uniones pegadas con la resina
especial a la madera \(B\), encontrando que la tensión promedio de corte
y desviación estándar fueron de \(1010_{psi}\) y \(380_{psi}\).
Si se asume que la tensión sobre la unión pegada con la resina
experimental en cada clase de madera se distribuye aproximadamente
normal con varianzas diferentes. Emplee un nivel de significancia del
\(8\%\) para observar si existen o no diferencias significativas de la
tensión promedio de corte de las dos marcas de madera.
Solución
El juego de hipótesis en esta dado por \[\begin{align*}
H_0:\mu_A - \mu_B = 0\\
H_1:\mu_A - \mu_B \neq 0\\
\end{align*}\] debido a que se quiere probar si hay o no diferencias
significativas entre las tensiones promedio de corte de las dos marcas
de madera. Adicionalmente, debido a que estamos en una situación en la
cual sabemos que las tensiones de corte se distribuyen normalmente con
varianzas diferentes pero desconocidas, se tendrá que estamos en una
situación dada por
situación que posee el siguiente estadístico de prueba \[\begin{align*}
t_c = \frac{(\bar{X}_A-\bar{X}_B) - d_0}{\sqrt{\frac{S^2_A}{n_A}+\frac{S^2_B}{n_B}}} \sim t_v
\end{align*}\]
En donde se observa que requerimos de los tamaños muestrales \(n_A=18\)
y \(n_B=12\), de las medias muestrales de \(\bar{X}_A=1130_{psi}\) y
\(\bar{X}_B=1010_{psi}\) junto a unas desviaciones estándar de
\(S_A=420_{psi}\) y \(S_B=380_{psi}\). Adicionalmente se requiere el
valor de los grados de libertad \(\nu\), los cuales están dados por
\[\begin{align*}
\nu &= \frac{\left(\frac{S^2_A}{n_A} + \frac{S^2_B}{n_B}\right)^2}{\frac{(S^2_A/n_A)^2}{n_A-1} + \frac{(S^2_B/n_B)^2}{n_B-1}} \\
&= \frac{\left(\frac{420^2}{12} + \frac{380^2}{18}\right)^2}{\frac{(480^2/12)^2}{12-1} + \frac{(380^2/18)^2}{18-1}} \\
&= \frac{476694444}{18813149} \\
&= 25.33837
\end{align*}\]
Al calcular el valor techo de \(\nu\) tendremos que \[\begin{align*}
\nu &= 25.33837 \\
\lceil \nu \rceil &= \lceil25.33837\rceil \\
\lceil \nu \rceil &= 26
\end{align*}\]
y por tanto, al reemplazar todos los valores necesarios para realizar el
estadístico de prueba se tendrá que \[\begin{align*}
t_c &= \frac{(1130-1010) - 0}{\sqrt{\frac{420^2}{18}+\frac{380^2}{12}}} \\
&= 0.8121219
\end{align*}\]
Ahora, para llevar a cabo la decisión, se decide emplear el P-valor, el
cual es igual a \[\begin{align*}
P-valor &= 2\mathbb{P}(t_nu > |t_c|)
\end{align*}\]
En donde, al aplicar la función de Excel 1 -
DISTR.T.N(ABS(0.8121219); 26; VERDADERO), se tendrá que
\[\begin{align*}
P-valor &= 2\mathbb{P}(t_nu > |t_c|) \\
&= 2(0.212047625) \\
&= 0.4240952
\end{align*}\]
Encontrando que el P-valor es superior al nivel de significancia del
\(8\%\), lo cual significa que no hay evidencia suficiente para rechazar
la hipótesis nula y por tanto se concluirá que no existen diferencias
significativas entre las tensiones promedio de corte de las dos marcas
de madera.
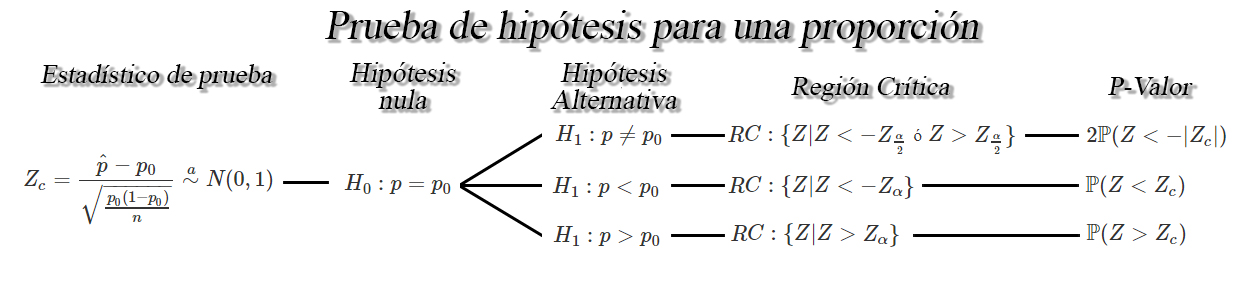
Prueba de hipótesis para una proporción $p$
Sea $X_1,X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$, tal que $X\sim b(n,p)$ entonces si $n$ es suficientemente
grande tal que $n\geq30$, y la proporción desconocida $p$ no se
encuentre cercana a $0$ o $1$, tal que $np>5$ y $n(1-p)>5$,
entonces un una prueba de hipótesis para la proporción verdadera $p$
será de la forma
Ejercicio
Suponga que se realiza un estudio sobre los costos que han tenido proyectos de renovación de parques en la ciudad de Medellín, encontrando que los costos asociados a \(20\) proyectos que se han llevado a cabo en la ciudad, en millones de pesos, fueron de
| 1780 | 2933 | 1220 | 1278 | 1170 | 1032 | 1245 | 2070 | 2040 | 1289 |
| 1531 | 980 | 1730 | 1380 | 2243 | 1687 | 1422 | 1731 | 1435 | 2080 |
Si se cree que la verdadera proporción de proyectos que poseen costos superiores a \(1900\) millones de pesos es de más del \(40\%\), emplee un nivel de significancia del \(5\%\) para probar si dicha creencia se encuentra apoyada por la información empírica.
Solución
En este caso estamos interesados en probar si la verdadera proporción de
proyectos que poseen costos superiores a \(1900\) millones de pesos es
de más del \(40\%\), y por tanto se tendrá que el juego de hipótesis
está dado por \[\begin{align*}
H_0:p \leq 0.40\\
H_1:p > 0.40
\end{align*}\]
Entonces como estamos interesados en hacer inferencia sobre una
proporción, y nos encontramos frente a una hipótesis unilateral,
tendremos que estamos ante la siguiente situación
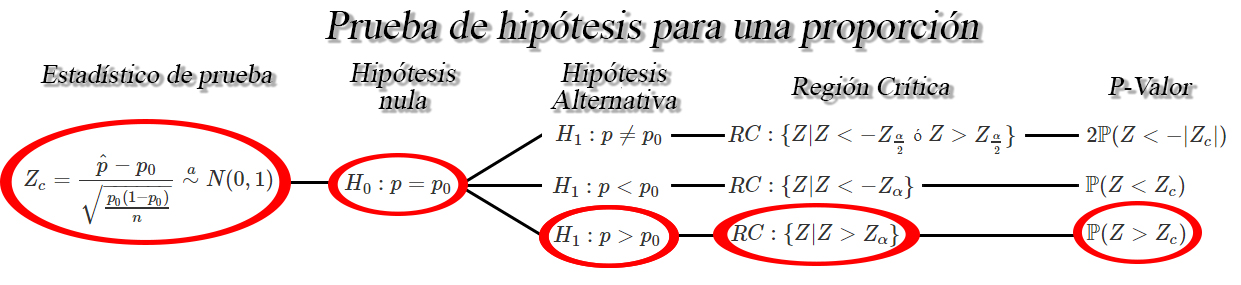En donde se observa que el estadístico de prueba está dado por
\[\begin{align*}
Z_c = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} \stackrel{a}{\sim} N(0,1)
\end{align*}\]
En donde se evidencia que necesitamos para el cálculo de la proporción
muestral de proyectos que poseen costos superiores a \(1900\) millones
de pesos, del tamaño de muestra \(n=20\) y de la proporción establecida
en la hipótesis nula.
Para realizar el cálculo de la
proporción muestral se trata de localizar aquellos costos que posean un
valor superior a \(1900\) millones de pesos, denotando como \(1\)
aquellas observaciones que sean superiores a \(1900\) millones de pesos,
y \(0\) aquellas observaciones que no cumplan la condición, tal que
\[\begin{align*}
\underset{0}{1780} \quad \underset{1}{2933} \quad \underset{0}{1220} \quad \underset{0}{1278} \quad \underset{0}{1170} \quad \underset{0}{1032} \quad \underset{0}{1245} \quad \underset{1}{2070} \quad \underset{1}{2040} \quad \underset{0}{1289} \\
\underset{0}{1531} \quad \underset{0}{980} \quad \underset{0}{1730} \quad \underset{0}{1380} \quad \underset{1}{2243} \quad \underset{0}{1687} \quad \underset{0}{1422} \quad \underset{0}{1731} \quad \underset{0}{1435} \quad \underset{1}{2080}
\end{align*}\]
Al contar el número de éxitos, observamos que tenemos un total de
\(x=5\) éxitos en un total de \(n=20\) muestras, y por tanto, podemos
aplicar la fórmula de frecuencia relativa para calcular la proporción
muestral de egresados que poseen salarios superiores a \(1900\)
millones, tal que \[\begin{align*}
\hat{p} &= \frac{\text{# éxitos}}{\text{Total ensayos}} \\
&= \frac{x}{n} \\
&= \frac{5}{20} \\
&= 0.25
\end{align*}\]
Ahora, al emplear este valor a los ya mencionados para el cálculo del
estadístico de prueba, se tendrá que éste es igual a \[\begin{align*}
Z_c &= \frac{0.25 - 0.4}{\sqrt{\frac{0.4(1-0.4)}{20}}} \\
&= -1.369306
\end{align*}\]
En donde, se decide emplear el P-valor para observar si hay o no
evidencia a favor de la hipótesis nula, y para ello se emplea la función
de Excel 1 - DISTR.NORM.ESTAND.N(-1.369306;
VERDADERO) obteniendo que \[\begin{align*}
P-valor &= \mathbb{P}(Z>Z_c) \\
&= \mathbb{P}(Z>-1.369306)\\
&= 1 - \mathbb{P}(Z\leq -1.369306)\\
&= 0.9145482
\end{align*}\]
En donde se evidencia que el P-valor asociado al estadístico de prueba
posee un valor del \(91.45\%\) el cual es mayor al nivel de
significancia preestablecido de \(5\%\), permitiendo concluir que no se
rechaza la hipótesis nula, y por tanto, se tendrá que la verdadera
proporción de proyectos que poseen costos superiores a \(1900\) millones
de pesos no es mayor a \(40\%\).
Prueba de hipótesis para diferencia de proporciones $p_1 - p_2$
Sean $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias iid de
tamaño $n_1$ y $n_2$, tal que $X_{i}\sim b(n_i,p_i)$, para
$i=1,2$, entonces si $n_1$ y $n_2$ son suficientemente grandes tal
que $n_1, n_2\geq30$, y si las proporciones desconocidas $p_1$ y
$p_2$ no se encuentran cercanas a $0$ o $1$, tal que $n_ip_i>5$
y $n_i(1-p_i)>5$, para $i=1,2$, entonces un una prueba de hipótesis
para la diferencia de las proporciones $p_1-p_2$ será de la forma
Ejercicio
Una empresa de computación decide realizar un cambio en el proceso de
fabricación de uno de los componentes que requiere en sus portátiles, y
está en interesado en saber si dicho cambio ofrece una mejora
significativa en la rendimiento que sus equipos ofrecen.
Para
determinar si el cambio en el proceso de fabricación mejora el
rendimiento que sus equipos ofrecen, deciden tomar una muestra de
equipos antes y después de la implementación del nuevo proceso de
fabricación y se evalúa la velocidad de procesamiento para la ejecución
de un programa determinado. Suponga que se encuentra que \(120\) de
\(500\) computadores fabricados con el método actual ofrece un
rendimiento superior al promedio, mientras que, \(220\) de \(700\)
computadores fabricados con el nuevo método ofrece un rendimiento
superior al promedio.
Basados en la información obtenida,
emplee un nivel de confianza del \(2\%\) para probar si la proporción de
nuevos equipos que ofrecen un rendimiento superior al promedio, es igual
o superior a la proporción de equipos actuales que ofrecen un
rendimiento superior al promedio.
Solución
Como estamos interesado en comparar la proporción de rendimiento
superior al promedio entre los nuevos equipos y los actuales, para saber
si los nuevos equipo son iguales o superiores a los actuales, tendremos
que la hipótesis de interés está dada por \[\begin{align*}
H_0:p_N - p_A \geq 0\\
H_1:p_N - p_A < 0
\end{align*}\]
Entonces como estamos interesados en hacer inferencia sobre una
diferencia de proporciones, y nos encontramos frente a una hipótesis
unilateral, tendremos que estamos ante la siguiente situación
En donde se observa que el estadístico de prueba está dado por
\[\begin{align*}
Z_c = \frac{(\hat{p}_N - \hat{p}_A) - d_0}{\sqrt{\frac{p^*(1-p^*)}{n_N} + \frac{p^*(1-p^*)}{n_A}}} \stackrel{a}{\sim} N(0,1)
\end{align*}\]
De lo anterior se observa que para el cálculo se requiere de las
proporciones muestrales \(\hat{p}_{N}\) y \(\hat{p}_{A}\), y
proporciones conjuntas \(p^*\), las cuales se pueden obtener a partir
del tamaño de muestra y del número de éxitos obtenidos, tal que para el
caso de los equipos construidos con el nuevos procedimiento se tendrá
que \[\begin{align*}
\hat{p}_N &= \frac{\text{# de equipos nuevos con rendimiento superior}}{\text{Total equipos nuevos evaluados}} \\
&= \frac{x_N}{n_N} \\
&= \frac{220}{700} \\
&= 0.3142857
\end{align*}\]
mientras que para los equipos que se construyen con el procedimiento
actual, se tendrá que
\[\begin{align*}
\hat{p}_A &= \frac{\text{# de equipos actuales con rendimiento superior}}{\text{Total equipos actuales evaluados}} \\
&= \frac{x_A}{n_A} \\
&= \frac{120}{500} \\
&= 0.24
\end{align*}\]
Ahora, la proporción conjunta es igual a \[\begin{align*}
p^* &= \frac{x_N + x_A}{n_N + n_A} \\
&= \frac{220 + 120}{700 + 500} \\
&= 0.2833333
\end{align*}\]
Una vez calculados todos los valores asociados al estadístico de prueba,
se procede a su cálculo, el cual está dado por \[\begin{align*}
Z_c &= \frac{(0.3142857 - 0.24) - d_0}{\sqrt{\frac{0.2833333(1-0.2833333)}{700} + \frac{0.2833333(1-0.2833333)}{500}}} \\
&= 2.815407
\end{align*}\]
Ahora, con el fin de decidir si el estadístico de prueba apoya o no la
hipótesis establecida, se emplea en esta ocasión la región crítica la
cual estará dada por \[\begin{align*}
RC:\{Z|Z<-Z_{\alpha}\}
\end{align*}\]
en donde al emplear la función de Excel
INV.NORM.ESTAND(1-\(\alpha\)) encontraríamos que el valor
crítico \(Z_{\alpha=0.02}=2.053749\) y por tanto la región crítica será
\[\begin{align*}
RC:\{Z|Z<-2.053749\}
\end{align*}\]
Entonces como el estadístico de prueba no cae dentro de la región
crítica, no hay evidencia significativa en contra de la hipótesis nula,
y por tanto se tendrá que la proporción de nuevos equipos que ofrecen un
rendimiento superior al promedio no es inferior a la proporción de
equipos fabricados con el actual proceso que ofrecen rendimientos
superiores al promedio.
Prueba de hipótesis para una varianza $\sigma^2$
Sea $X_{1}, X_{2}, \ldots, X_{n}$ una muestra aleatoria de una
problación normal de tamaño $n$ conmedias $\mathbb{E}(X)=\mu$ y
varianza desconocidas $Var(X)=\sigma_1^2<\infty$, entonces un
contraste de hipótesis para la varianza real $\sigma^2$, a un nivel de
significancia $\alpha$ será de la forma
Ejercicio
Suponga que se realiza un estudio sobre los costos que han tenido proyectos de renovación de parques en la ciudad de Medellín, encontrando que los costos asociados a \(20\) proyectos que se han a cabo en le ciudad, en millones de pesos, fueron de
| 1780 | 2933 | 1220 | 1278 | 1170 | 1032 | 1245 | 2070 | 2040 | 1289 |
| 1531 | 980 | 1730 | 1380 | 2243 | 1687 | 1422 | 1731 | 1435 | 2080 |
Si es posible supone que el costo de construir cualquier parque se distribuyen aproximadamente normal, emplee un nivel de significancia del \(5\%\) para observar si la variabilidad de los costos de cualquier construcción es de al menos \(300000\) millones de pesos\(^2\).
Solución
Como estamos interesados en este punto de observar si la variabilidad de
los costos de cualquier construcción es de al menos \(300000\) millones
de pesos\(^2\) y por tanto la hipótesis de interés está dada por
\[\begin{align*}
H_0:\sigma^2 \geq 300000\\
H_1:\sigma^2 < 300000
\end{align*}\]
En donde, se evidencia que en este caso estaremos bajo la siguiente
situación
la cual muestra que el estadístico de prueba en esta ocasión está dada
por \[\begin{align*}
\chi^2_c = \frac{(n-1)S^2}{\sigma^2_0} \sim \chi^2_{n-1}
\end{align*}\]
De lo anterior, se observa que para el cálculo del estadístico de
prueba, se requiere de la varianza muestral \(S^2 = 230541.2\), el
tamaño de muestra \(n=20\) y el valor de la hipótesis nula, en donde, al
reemplazar dichos valores en el estadístico de prueba se tendrá que
\[\begin{align*}
\chi^2_c &= \frac{(20-1)230541.2}{300000} \\
&= 14.60094
\end{align*}\]
en donde, al estar frente a una situación unilateral izquierda, se
tendrá que el P-valor para este caso está dado por \[\begin{align*}
P-valor = \mathbb{P}(\chi^2_{n-1}<\chi^2_c)
\end{align*}\]
Entonces, al emplear la función de Excel
DISTR.CHICUAD(14.60094; 20-1; VERDADERO) se tiene que $$$$
Entonces, como el P-valor obtenido es superior al nivel de significancia
preestablecido del \(5\%\), se concluye que no hay evidencia suficiente
para rechazar la hipótesis nula, y por tanto, se tendrá que la
variabilidad de los costos de cualquier construcción es de al menos
\(300000\) millones de pesos\(^2\).
Prueba de hipótesis para cociente de varianzas $\sigma^2_1/\sigma^2_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias normales
de tamaños $n_1$, y $n_2$ con medias $\mathbb{E}(X_{1})=\mu_1$ y
$\mathbb{E}(X_{2})=\mu_2$, y varianzas desconocidas
$Var(X_{1})=\sigma_1^2<\infty$ y $Var(X_{2})=\sigma^2_2<\infty$,
respectivamente, entonces un contraste de hipótesis para el cociente de
varianzas $\sigma^2_1/\sigma^2_2$, a un nivel de significancia
$\alpha$ será de la forma
Ejercicio
Se aplican pruebas a \(10\) cables conductores soldados a un dispositivo semiconductor con el fin de determinar su resistencia a la tracción. Las pruebas demostraron que para romper la unión se requiere las libras de fuerza que se listan a continuación.
| Sin Encapsulado | 19.8 | 12.7 | 13.2 | 16.9 | 10.6 | 18.8 | 11.1 | 14.3 | 17.0 | 12.5 |
Otra conjunto de \(8\) cables conductores que forman otro dispositivo, se encapsulan y se prueban para determinar si el encapsulado aumenta la resistencia a la tracción, obteniendo para este caso se requirieron las siguientes libras de fuerza para romper la unión
| Con Encapsulado | 24.9 | 22.9 | 23.6 | 22.1 | 20.3 | 21.6 | 21.9 | 22.5 |
Si se supone que las resistencias a la tracción se distribuyen normalmente, construya un intervalo del \(90\%\) para la razón de varianzas entre la variabilidad de los cables sin encapsulado y la variabilidad de los cables con encapsulado. Es posible afirmar que la variabilidad de de los cables con encapsulado es superior a los cables sin encapsulado?
Solución
En este punto nos mencionan que se tiene interés en calcular un
intervalo de confianza para el cociente de las varianzas asociadas a la
resistencia a la tracción para cables sin encapsulado y cables con
encapsulado. Además nos mencionan que la resistencia a la tracción hasta
la ruptura se distribuye normalmente, y por tanto deberemos calcular el
siguiente intervalo
en donde se aprecia que el intervalo bilateral para la razón de
varianzas posee la estructura \[\begin{align*}
\frac{S^2_C}{S^2_S}\frac{1}{f_{\alpha/2, n_C-1, n_S-1}} < \frac{\sigma^2_C}{\sigma^2_S} < \frac{S^2_C}{S^2_S}f_{\alpha/2, n_S-1, n_C-1}
\end{align*}\]
En donde se observa que para realizar el cálculo del intervalo, se
requiere de los varianzas muestrales \(S^2_S\) y \(S^2_C\), el nivel de
confianza \(1-\alpha\) y los valores críticos
\(f_{\alpha/2, n_C-1, n_S-1}\) y \(f_{\alpha/2, n_S-1, n_C-1}\).
Para realizar el cálculo de las varianzas muestrales, se emplean
los datos muestrales y los tamaños de muestra \(n_C=8\) y \(n_S=10\),
tal que al realizar el cálculo obtenemos
\[\begin{align*}
S^2_C = 1.378146 \quad \text{ y } \quad S^2_S = 3.231254
\end{align*}\]
Por su parte, al buscar los valores críticos para un nivel de
significancia \(1-\alpha=0.90\) y tamaños muestrales \(n_C=8\) y
\(n_S=10\) tenemos que
\[\begin{align*}
f_{\alpha/2 = 0.05, n_C-1 = 7, n_S-1 = 9} = 3.292746\\
f_{\alpha/2 = 0.05, n_S-1 = 9, n_C-1 = 7} = 3.676675
\end{align*}\]
Una vez calculados los valores necesarios para calcular el intervalo de
confianza, se procede a su cálculo, tal que \[\begin{align*}
\frac{1.378146}{3.231254}\frac{1}{3.292746} &< \frac{\sigma^2_C}{\sigma^2_S} < \frac{1.378146}{3.231254}3.676675 \\
0.1295287 &< \frac{\sigma^2_C}{\sigma^2_S} < 1.56812
\end{align*}\]
Por tanto, se podrá concluir con un nivel de confianza del \(90\%\) que
el verdadero valor para el cociente de varianzas entre la variabilidad
de los cables sin encapsulado y la variabilidad de los cables con
encapsulado, se encontrará entre \(0.1295287\) y \(1.56812\).
Ahora, para verificar si existen o no diferencias significativas entre
las varianzas de resistencia a la tracción de los cables encapsulados o
sin encapsular, debemos verificar la posición en la que se encuentra el
intervalo de confianza para la razón de varianzas
\(\sigma^2_C/\sigma^2_S\).
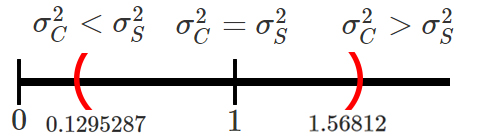En donde se observa que el intervalo calculado contiene el valor de
\(1\), el cual representa la igualdad entre la varianza de los dos tipos
de cable, tal que \[\begin{align*}
\sigma^2_C = \sigma^2_S \quad =>\quad \frac{\sigma^2_C}{\sigma^2_S} = 1
\end{align*}\]
y por tanto, con un nivel de confianza del \(90\%\) no será posible
afirmar que la variabilidad de la resistencia a la tracción de los
cables encapsulados o sin encapsular sean diferentes, y por tanto, debe
asumirse que éstos son iguales.
Estimación por intervalos
Podría ser que ni el estimador que cumpla las propiedades de insesgadez, eficiencia, consistencia y suficiencia, estimen con exactitud el parámetro poblacional de interés y por esta razón, puede ser preferible determinar un intervalo dentro del cual, se espera encontrar el valor verdadero del parámetro poblacional.
Definición
Sea $\theta$ un parámetro poblacional desconocido, entonces basándose
en la información de una muestra aleatoria de dicha población, el
objetivo será encontrar dos variables aleatorias $\hat{\Theta}_I$ y
$\hat{\Theta}_S$ tal que
\begin{align*} \mathbb{P}(\hat{\Theta}_I<\Theta<\hat{\Theta}_S) = 1-\alpha \quad \quad 0<\alpha<1 \end{align*}
donde $(1-\alpha)$ se conoce como nivel de confianza y
$\hat{\Theta}_I$ y $\hat{\Theta}_S$ se denominan como límites de
confianza inferior y superior, tal que
$\hat{\Theta}_I<\hat{\Theta}_S$.
Nota
- Usualmente se usan valores para \(\alpha\) de \(0.1, 0.05\) y $ 0.01$, es decir, niveles de confianza de \(0.9, 0.95\) y \(0.99\).
- La longitud o amplitud del intervalo construido, medirá la precisión de la estimación realizada, por tanto, intervalos largos proporcionan estimaciones más imprecisas, mientras que intervalos cortos proporcionan estimaciones más precisas.
- A medida que aumenta el nivel de confianza, la amplitud del intervalo se hace más grande.
- A medida que aumenta el tamaño de muestra, la amplitud del intervalo se hace más pequeño.
Interpretación de nivel de confianza
El nivel de confianza, $1-\alpha$, mide la fiabilidad del intervalo de
probabilidad, esto es, la probabilidad de que el verdadero valor del
parámetro se encuentre dentro del intervalo construido. Es decir, que si
se realiza el experimento muchas veces, se tendrá que en el
$100(1-\alpha)\%$ de los intervalos de confianza construidos en cada
experimento, se encontrará contenido el verdadero valor del parámetro de
interés.
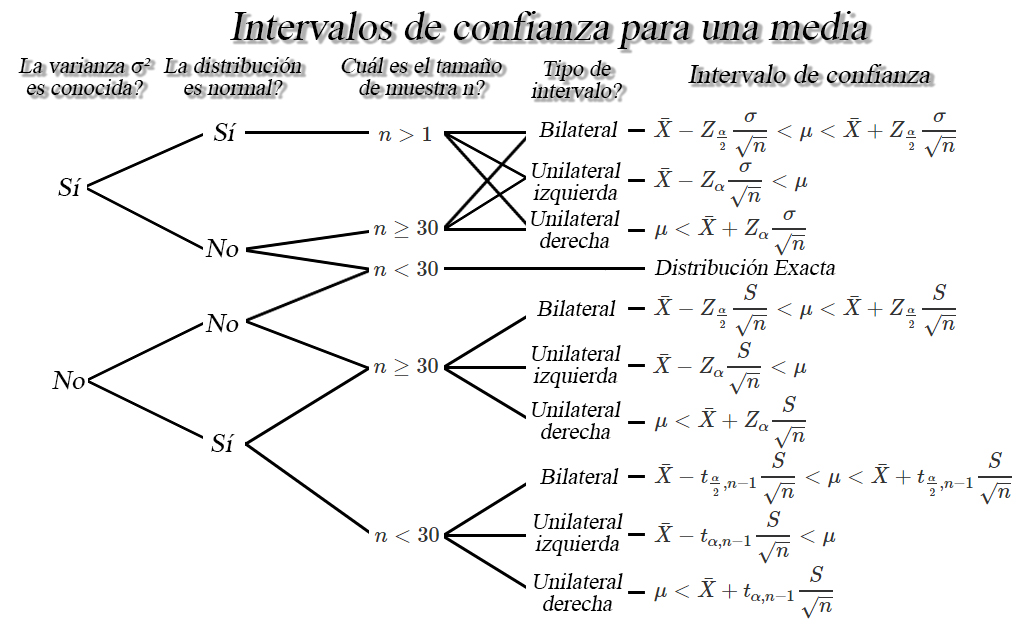
Intervalos de confianza para una media $\mu$
Sea $X_1, X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$ con media desconocida $\mathbb{E}(X)=\mu$, y varianza
$Var(X)=\sigma^2<\infty$, entonces dependiendo de las condiciones, se
tendrán los siguientes intervalos de confianza para la media $\mu$.
Ejercicio
Suponga que se realiza un estudio sobre los costos que han tenido proyectos de renovación de parques en la ciudad de Medellín, encontrando que los costos asociados a \(20\) proyectos que se han llevado a cabo en le ciudad, en millones de pesos, fueron de
| 1780 | 2933 | 1220 | 1278 | 1170 | 1032 | 1245 | 2070 | 2040 | 1289 |
| 1531 | 980 | 1730 | 1380 | 2243 | 1687 | 1422 | 1731 | 1435 | 2080 |
Si es posible supone que el costo de construir cualquier parque se distribuyen aproximadamente normal, calcule el límite superior del costo promedio de construir cualquier parque empleando un nivel de confianza del \(98\%\).
Solución
En este caso estamos interesados en construir un intervalo de confianza
para el límite superior del costo promedio de construir cualquier
parque, pero para realizar el cálculo debemos tener en cuenta la
información que poseemos.
De la información extraída del
enunciado tenemos que la varianza poblacional no es conocida, ya que no
la mencionan en el enunciado, tenemos que la población es normal, debido
a que mencionan que puede suponerse que los salarios son aproximadamente
normales, y los tamaños de muestra son pequeños, debido a que solo
tenemos \(20\) datos, estas características se ilustra en la siguiente
imagen
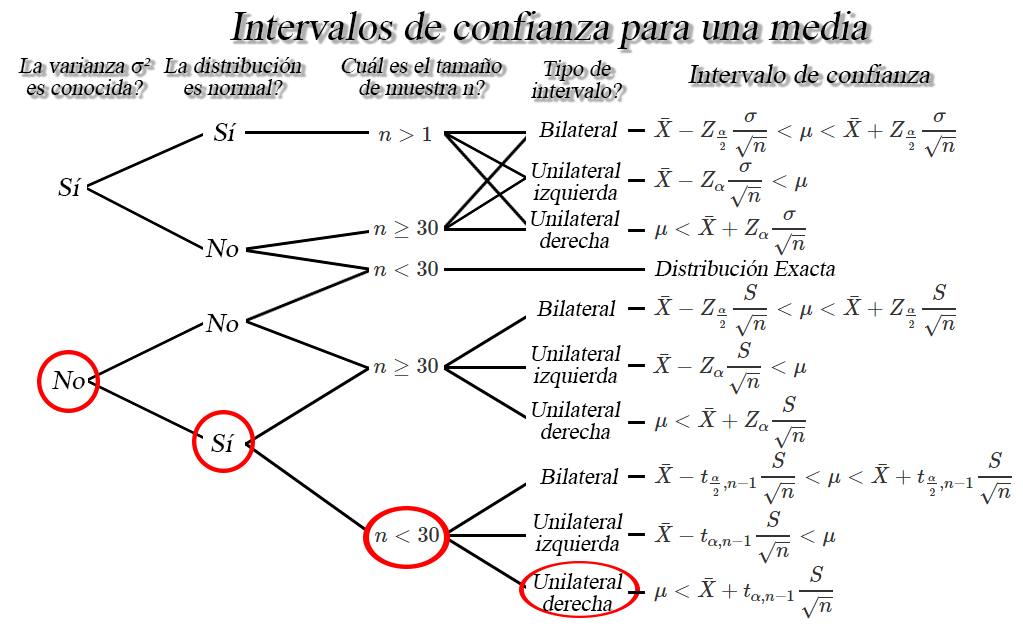de lo anterior encontramos que el intervalo de confianza de interés es
de la forma \[\begin{align*}
\mu < \bar{X}+t_{\alpha, n-1}\frac{S}{\sqrt{n}}
\end{align*}\]
En donde observamos que requerimos de \(5\) variables, la media muestral
\(\bar{X}=1613.8\), la desviación estándar muestral \(S=480.1471\), el
tamaño de muestra \(n=20\), el nivel de confianza \(1-\alpha=0.98\) y el
valor crítico \(t_{\alpha=0.02, n-1=19}=2.204701\) calculado a partir
del nivel de confianza y el tamaño de la muestra. Al reemplazar en el
intervalo tenemos que \[\begin{align*}
\mu &< 1613.8+2.204701\frac{480.1471}{\sqrt{20}}\\
\mu &< 1613.8+236.7059\\
\mu &< 1850.506
\end{align*}\]
Entonces podremos afirmar con un nivel de confianza del \(98\%\), que el
costo máximo promedio que puede constar un construir cualquier parque es
de \(1850.506\) millones de pesos, es decir, mil ochocientos cincuenta
millones y quinientos seis mil pesos.
Ejercicio
Suponga que Postobon desarrolla una nueva máquina de bebidas para servir
de forma automática gaseosas en los cines, de tal forma que la cantidad
servida, en mililitros, se distribuye Weibull con varianza de
\(5703.473_{ml}\).
Si se decide tomar una muestra aleatoria de
\(8000\) vasos de gaseosa servidos por una de las nuevas máquinas de
bebidas, y se obtiene una promedio de \(345_{ml}\) con una varianza de
\(5240.35_{ml^2}\), construya un intervalo de confianza del \(90\%\)
para la verdadera cantidad promedio de refresco servida por la máquina.
Solución
En este caso estamos interesados en construir un intervalo de confianza
bilateral del $90% $ para la cantidad promedio de refresco servida por
la nueva máquina de bebidas, pero para realizar el cálculo debemos
evaluar previamente la información que poseemos.
Del contexto
del ejercicio tenemos que la población no es normal, debido a que se
menciona que es Weibull, con varianza de \(5703.473_{ml^2}\), por lo
cual tendremos que la varianza poblacional es conocida. Adicionalmente,
tenemos que el tamaño de muestra de vasos de gaseosa servidos por la
máquina es de \(8000\) vasos, por lo cual, basados en la información que
poseemos tenemos las siguientes características
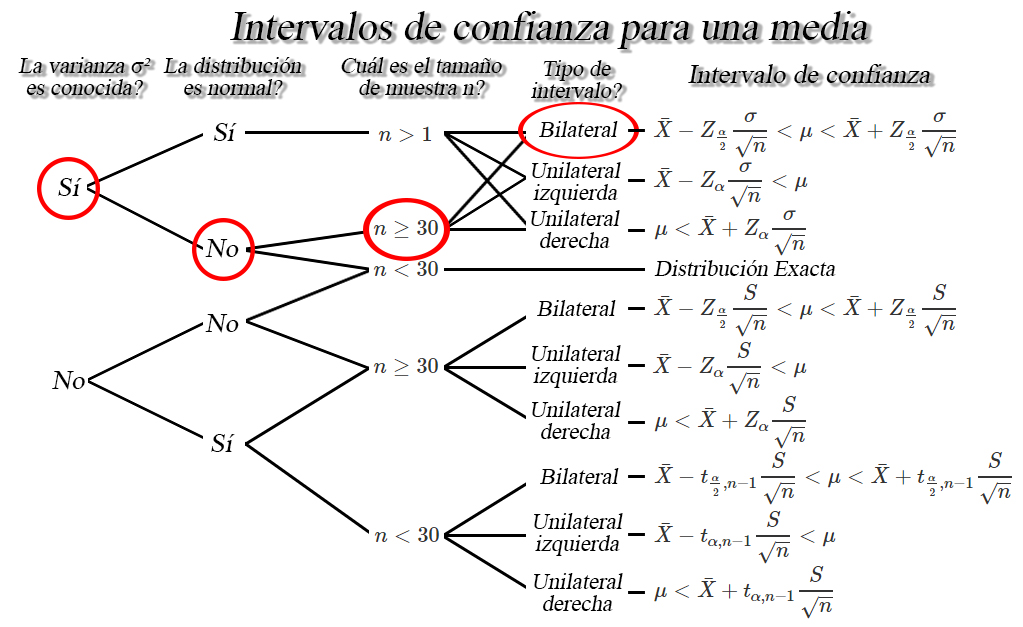de lo anterior encontramos que el intervalo de confianza de interés es
de la forma \[\begin{align*}
\bar{X}-Z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}} < \mu < \bar{X}+Z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}
\end{align*}\]
En donde observamos que requerimos la media muestral \(\bar{X}=345\), la
desviación estándar poblacional \(\sigma=75.52134\), el tamaño de
muestra \(n=8000\), el nivel de confianza \(1-\alpha=0.90\) y el valor
crítico \(Z_{\alpha/2=0.05}=1.644854\) calculado a partir del nivel de
confianza. Al reemplazar en el intervalo tenemos que \[\begin{align*}
&345\pm 1.644854 \frac{75.52134}{\sqrt{8000}} \\
&345\pm 1.388839 \\
&343.6112 < \mu < 346.3888
\end{align*}\]
Entonces podremos afirmar con un nivel de confianza del \(90\%\), que la
cantidad promedio de refresco servida de forma automática por la nueva
máquina de bebidas se encontrará entre \(343.6112_{ml}\) y
\(346.3888_{ml}\).
Ejercicio
Suponga que la marca de cigarrillo Malboro es auditada debido a que se
afirma que sus registros están adulterados. Ante ésto, el presidente de
la empresa asegura que sus registros son correctos y que el flujo de
caja promedio mensual que registran es de \(25\) mil millones. Para
probar si dicha afirmación es posible, el auditor decide revisar el
flujo de caja de la empresa de los últimos \(48\) meses encontrando que
el flujo de caja promedio que registra la empresa es de \(21.389\) mil
millones de pesos con una desviación estándar de \(3.213\) mil millones
de pesos.
Si puede suponerse que el flujo de caja de la
empresa Malboro se distribuye normalmente, calcule con un nivel de
confianza del \(95\%\) para el verdadero flujo de caja promedio que
posee la empresa Malboro. Hay evidencia para pensar que la afirmación
del presidente es acertada?.
Solución
En este ejercicio se está interesado en construir un intervalo de
confianza bilateral del \(95\%\) para el flujo de caja promedio que
posee la empresa Malboro, y para realizar el cálculo debemos evaluar la
información que poseemos.
Entre la información suministrada
tenemos que la distribución de probabilidad del flujo de caja de la
empresa se distribuye normalmente, con varianza poblacional desconocida.
Además, mencionan que en entre la información recolectada por el auditor
encontró que de una muestra aleatoria de tamaño \(48\) meses, se
encontró que el flujo de caja promedio fue de \(21.389\) mil millones de
pesos con una desviación estándar de \(3.213\) mil millones de pesos, y
en consecuencia nos encontramos en la siguiente situación
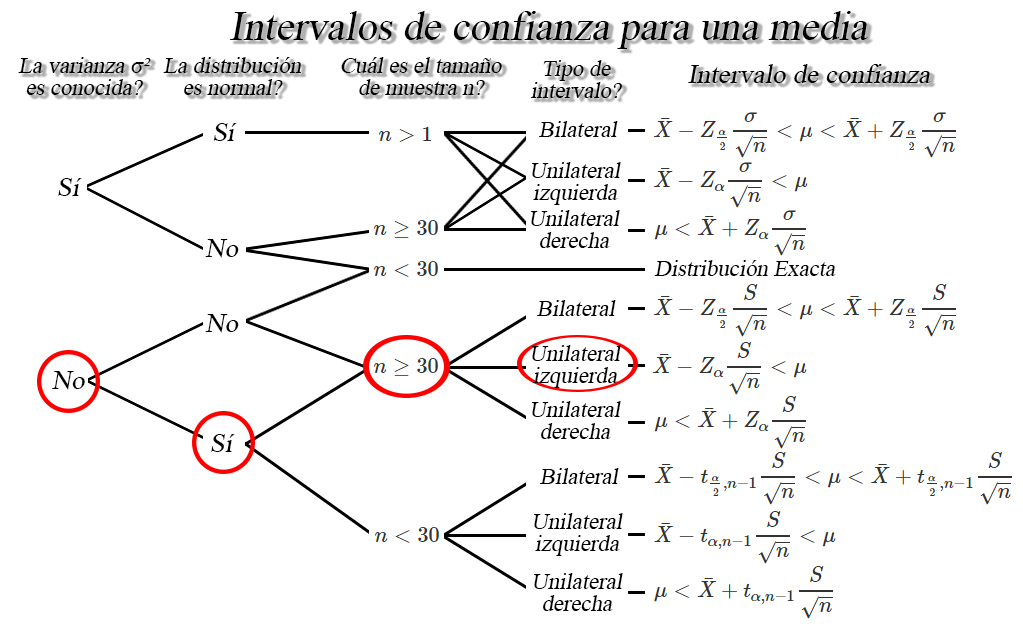de lo anterior encontramos que el intervalo de confianza de interés es
de la forma \[\begin{align*}
\bar{X}-Z_{\alpha}\frac{S}{\sqrt{n}} < \mu
\end{align*}\]
En donde observamos que necesitamos la media muestral
\(\bar{X}=21.389\), la desviación estándar muestral \(S=3.213\), el
tamaño de muestra \(n=48\), el nivel de confianza \(1-\alpha=0.95\) y el
valor crítico \(Z_{\alpha=0.05}=1.644854\) calculado a partir del nivel
de confianza. Al reemplazar en el intervalo de interés tenemos que
\[\begin{align*}
21.389 &\pm 1.644854 \frac{3.213}{\sqrt{48}}\\
21.389 &\pm 0.763 \\
20.626 &< \mu < 22.152
\end{align*}\]
Lo cual significa que, con un nivel de confianza del \(95\%\) podemos
afirmar que la afirmación del presidente no es acertada, debido a que el
verdadero flujo promedio que posee la empresa se encontrará entre
\(20.626\) mil millones de pesos y \(22.152\) mil millones de pesos, lo
cual se encuentra por debajo del valor afirmado.
Intervalos de confianza para diferencia de medias $\mu_1 - \mu_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_2}$ dos muestras aleatorias iid de
tamaños $n_1$, y $n_2$ con medias desconocidas
$\mathbb{E}(X_{1})=\mu_1$ y $\mathbb{E}(X_{2})=\mu_2$, y varianzas
$Var(X_{1})=\sigma_1^2<\infty$ y $Var(X_{2})=\sigma^2_2<\infty$,
respectivamente, entonces dependiendo de las condiciones, se tendrán los
siguientes intervalos de confianza para la diferencia de medias
$\mu_1 - \mu_2$.
Ejercicio
Una empresa de electrodomésticos desea saber si los cursos de
capacitación sirven para mejorar el nivel de ventas de sus trabajadoras
y para ello decide enviar a \(12\) de sus agentes de ventas a dicho
curso. Una vez finalizado el curso, la empresa encuentra que estos
agentes generan unas ventas promedio de de \(43.5\) millones de pesos
con una desviación estándar de \(3.1\) millones de pesos.
Con
el fin de observar si el curso es o no efectivo, la empresa extrae una
muestra aleatoria independiente de \(15\) agentes que no asistieron a la
capacitación y encontró que las ventas promedio generadas y su
desviación estándar para estos agentes fue de \(40.8\) y \(2.3\)
millones de pesos respectivamente.
Si es posible suponer que
las poblaciones se distribuyen normalmente con varianzas iguales a
\(5.6\) millones de pesos\(^2\) para quienes se capacitaron y a \(4.3\)
millones de pesos\(^2\) para quienes no se capacitaron, construya un
intervalo de confianza del \(90\%\) para la diferencia entre los
promedios de ventas de los dos grupos. Es posible pensar que los cursos
de capacitación mejoran el promedio de ventas sobre quienes no
recibieron estos cursos?
Solución
En este ejercicio estamos interesados en construir un intervalo de
confianza bilateral para la diferencia entre el promedio de ventas de
las personas que asisten a un curso de capacitación, respecto a las
personas que no asisten a dicho curso, y para ello debemos revisar la
información presentada en el enunciado.
En donde, se observa
que nos dan el valor de las medias y desviaciones estándar muestrales
para cada uno de los grupos, además nos menciona que las poblaciones se
distribuyen normalmente con varianzas poblacionales conocidas e iguales
a \(5.6\) millones de pesos\(^2\) para quienes se capacitaron y a
\(4.3\) millones de pesos\(^2\) para quienes no se capacitaron, y por
tanto estamos en la situación
y por tanto como el intervalo es bilateral, el calculo que debemos hacer
tendrá la forma \[\begin{align*}
(\bar{X}_C-\bar{X}_S) \pm Z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2_C}{n_C}+\frac{\sigma^2_S}{n_S}}
\end{align*}\]
Para realizar el cálculo requerimos de las media muestrales
\(\bar{X}_C=43.5\) y \(\bar{X}_S=40.8\), las varianzas poblacionales
\(\sigma^2_C=5.6\) y \(\sigma^2_S=4.3\), los tamaños de muestrales
\(n_C=12\) y \(n_S=15\), el nivel de confianza \(1-\alpha=0.90\) y el
valor crítico \(Z_{\frac{\alpha}{2}=0.05}=1.644854\) calculado a partir
del nivel de confianza. Al reemplazar en el intervalo tenemos que
\[\begin{align*}
&(43.5-40.8) \pm 1.644854\sqrt{\frac{5.6}{12}+\frac{4.3}{15}} \\
&2.7 \pm 1.644854(0.8679478) \\
&2.7 \pm 1.427647 \\
&1.272353 < \mu_C - \mu_S < 4.127647
\end{align*}\]
Entonces podremos afirmar con un nivel de confianza del \(90\%\), de que
la diferencia entre el promedio de ventas de las personas que asisten a
un curso de capacitación, respecto a las personas que no asisten a dicho
curso de capacitación, se encuentra entre \(1.272353\) y \(4.127647\)
millones de pesos.
Ahora, para saber si la capacitación mejora
o no las ventas hay que tener en cuenta la posición en la que se
encuentre el intervalo para la diferencia entre \(\mu_C - \mu_S\).
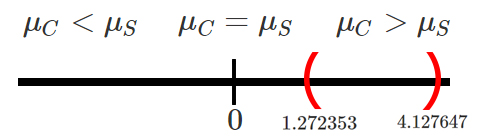En donde se observa que la totalidad del intervalo se encuentra
localizado en la sección que es mayor a \(0\), lo cual indica que para
todo el intervalo de confianza del \(90\%\) el promedio de ventas del
grupo que recibió un curso de capacitación \(\mu_C\) es mayor al
promedio de quienes no recibieron capacitación \(mu_S\), y por tanto, se
podrá concluir que la capacitación si mejora el promedio de ventas y se
recomendará a la empresa que envíe a capacitación al resto de empleados.
Ejercicio
La gobernación de Antioquia, desea construir un nuevo puente para
comunicar el municipio de Itagüí con Envigado, y para ello tiene dos
posibles ubicaciones en los cuales puede llevar a cabo dicho proyecto.
Para decidir en cual de las dos ubicaciones llevar a cabo el proyecto
decide tomar muestras aleatorias de cada ubicación y mirar en cual de
los dos hay mayor aflucencia de vehículos.
De la ubicación
\(A\) se decide tomar una muestra aleatoria de \(22\) días y de la
ubicación \(B\) de \(28\) días encontrando respectivamente que el número
promedio de vehículos para cada ubicación fue de \(2359\) y \(2147\)
vehículos, con una desviación estándar de \(143\) y \(301\) vehículos.
Si puede asumirse que el número de vehículos en las dos zonas
se distribuye aproximadamente normal con varianzas iguales, construya un
intervalo de confianza del \(90\%\) para la diferencia promedio del
número de vehículo que transita por cada ubicación. Es posible pensar
que hay diferencias significativas entre el número de vehículos que
transita por cada ubicación? En cuál de las dos zonas aconsejaría a la
gobernación llevar a cabo la construcción del puente?.
Solución
En este enunciado estamos interesados en construir un intervalo de
confianza del \(90\%\) para la diferencia promedio del número de
vehículo que transita por cada ubicación. En donde, el intervalo de
confianza será bilateral debido a que no especifican que se debe
calcular el límite superior o inferior solamente. Para saber cuál es el
intervalo de interés, debemos revisar la información presentada en el
enunciado.
En el enunciado se aprecia que nos dan las medias y
desviaciones estándar muestrales para cada una de las ubicaciones,
obtenidos a partir de muestras de tamaños \(22\) y \(28\),
respectivamente, tal que, los vehículos fueron \(\bar{X}_A=2359\) y
\(\bar{X}_B=2147\), mientras que las desviaciones estándar fueron
\(S_A=143\) y \(S_B=301\). Además, se menciona que el número de
vehículos en las dos zonas se distribuye normalmente con varianzas
desconocidas pero iguales, y por tanto estaremos en la siguiente
situación
y por tanto como el intervalo es bilateral, el calculo que debemos hacer
tendrá la forma \[\begin{align*}
(\bar{X}_A-\bar{X}_B) \pm t_{\frac{\alpha}{2}, n_A+n_B-2}S_p\sqrt{\frac{1}{n_A}+\frac{1}{n_B}}
\end{align*}\]
En donde observamos que entre otros valores, requerimos calcular el
valor de la desviación estándar conjunta \(Sp\), la cual está dada por
\[\begin{align*}
Sp^2 &= \frac{(n_A-1)S^2_A + (n_B-1)S^2_B}{n_A+n_B-2} \\
&= \frac{(22-1)143^2 + (28-1)301^2}{22 + 28 - 2} \\
&= 59909.5
\end{align*}\] y por tanto \[\begin{align*}
Sp &= \sqrt{Sp^2} \\
&= \sqrt{59909.5} \\
&= 244.7642
\end{align*}\]
Ahora, los valores adicionales que se requieren para realizar el cálculo
del intervalo de confianza serán, las medias muestrales
\(\bar{X}_A=2359\) y \(\bar{X}_B=2147\), y los tamaños muestrales
\(n_A=22\) y \(n_B=28\), el nivel de confianza \(1-\alpha=0.90\) y el
valor crítico \(t_{\frac{\alpha}{2}=0.05, n_A+n_B-2 = 48}=1.677224\). Al
reemplazar estos valores en el intervalo de interés obtenemos que
\[\begin{align*}
&(2359-2147) \pm 1.677224(244.7642)\sqrt{\frac{1}{22}+\frac{1}{28}} \\
&212 \pm 1.677224(244.7642)(0.2849014)\\
&212 \pm 116.959 \\
&95.041 < \mu_A - \mu_B < 328.959
\end{align*}\]
Por tanto, con un nivel de confianza del \(90\%\) se tendrá que la
diferencia promedio del número de vehículo que transita por cada
ubicación se encontrará entre \(95.041\) y \(328.959\) vehículos al día.
Ahora, para saber si existe diferencias significativas entre
el número de vehículos que transitan por cada ubicación debemos tener en
cuenta la posición en la que se encuentre el intervalo para la
diferencia entre \(\mu_A - \mu_B\).
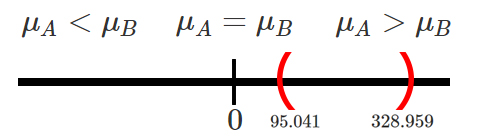En donde se observa que el intervalo encontrado se encuentra por encima
de \(0\), el cual simboliza que el número promedio de vehículos que
transitan por la ubicación \(A\) es superior que el número promedio de
vehículos que transitan por la ubicación \(B\), tal que \[\begin{align*}
\mu_A > \mu_B \quad =>\quad \mu_A - \mu_B > 0
\end{align*}\]
y por tanto, con un nivel de confianza del \(90\%\) es posible afirmar
que existen diferencias significativas entre el número de vehículos que
transitan por las dos ubicaciones, y por tanto se debería aconsejar a la
gobernación de Antioquia que construya el puente en la ubicación \(A\)
debido a que es por esta ubicación por donde hay mayor afluencias de
vehículos.
Ejercicio
Suponga que la Universidad de Antioquia adelanta un estudio sobre el
salario de sus egresados y desea comparar si es cierta la creencia que
las mujeres ganan en promedio menos dinero que los hombres.
Para comprobar si las creencias son ciertas, un grupo de investigación
de la Universidad toma una muestra representativa de \(250\) mujeres y
\(270\) hombres egresados de la Universidad y se les pregunta sobre cuál
es el salario que ganan actualmente, obteniendo en su investigación que
las mujeres ganan en promedio \(2.3\) millones de pesos con una
desviación estándar de \(0.7\) millones de pesos, mientras que los
hombres ganan en promedio \(2.6\) millones de pesos con una desviación
estándar de \(1.2\) millones de pesos.
Si el grupo de
investigación encuentra que los salarios no se distribuyen normalmente,
calcule el límite superior para la diferencia promedio del salario de
sus egresados hombres y egresados mujeres. Emplee un nivel de confianza
de \(80\%\).
Solución
En este enunciado estamos interesados en calcular el límite superior
para la diferencia promedio entre el salario de hombres y mujeres que
egresaron de la Universidad, la cual está dada por \(\mu_H - \mu_M\),
empleando para ello un nivel de confianza del \(80\%\). Ahora, para
identificar el intervalo de interés, debemos revisar la información
presentada por el grupo de investigación de la Universidad.
El
cual a partir de una muestra de \(250\) mujeres y \(270\) hombres,
encontró unos salarios promedios iguales a \(2.3\) y \(2.6\), con
desviaciones estándar de \(0.7\) y \(1.2\), respectivamente. Además
encuentra que los salarios no se distribuyen normalmente, y al no
mencionar cuales son las varianzas poblacionales, se asume que éstas no
son conocidas, y por tanto estaremos en la siguiente situación dado que
los tamaños muestrales son mayores a \(30\).
y por tanto al ser un intervalo unilateral derecho (límite superior), el
calculo que debemos hacer tendrá la forma \[\begin{align*}
\mu_H - \mu_M < (\bar{X}_H-\bar{X}_M) + Z_{\alpha}\sqrt{\frac{S^2_H}{n_H}+\frac{S^2_M}{n_M}}
\end{align*}\]
en donde se observa que al ser unilateral derecho, el intervalo solo
cuenta con la suma de la resta de medias muestrales y el término de
error, además de que, el valor crítico solo será para el valor
\(\alpha\), y no \(\alpha/2\) como es el caso de los intervalos
bilaterales.
Ahora, al reemplazar los valores encontrados por
el grupo de investigación \(n_H=270\), \(\bar{X}_H=2.6\), \(S_H=1.2\)
para los hombres, \(n_M=250\), \(\bar{X}_M=2.3\), \(S_M=0.7\) para las
mujeres, el nivel de confianza \(1-\alpha = 0.80\) y el valor crítico
\(Z_{\alpha=0.2}=0.8416212\), tendremos que \[\begin{align*}
&\mu_H - \mu_M < (2.6-2.3) + 0.8416212\sqrt{\frac{1.2^2}{270}+\frac{0.7^2}{250}} \\
&\mu_H - \mu_M < 0.3 + 0.8416212(0.08540101)\\
&\mu_H - \mu_M < 0.3 + 0.0718753 \\
&\mu_H - \mu_M < 0.3718753
\end{align*}\]
Por tanto, se tendrá que el valor máximo que se espera tener parar la
diferencia entre los salarios promedio de hombres y mujeres es de
\(0.3718753\) millones de pesos, lo anterior con un nivel de confianza
del \(80\%\).
Ejercicio
Se realiza un estudio con el fin de comparar el rendimiento de
combustible en kilómetros por galón para dos tipos de motores \(A\) y
\(B\). Suponga que se decide realizar un total de \(47\) experimentos
con el motor \(A\) y \(56\) experimentos con el motor \(B\), encontrando
para cada caso, un rendimiento promedio de gasolina de \(44\) y \(48\)
kilómetros, respectivamente, con desviaciones estándar de \(8.3\) y
\(6.6\), respectivamente.
Basados en la información anterior,
calcule el límite inferior para la diferencia promedio entre los
rendimiento de combustible en kilómetro por galón de gasolina para los
motores \(B\) y \(A\), empleando un nivel de confianza del \(88\%\).
Suponga que los rendimientos de los combustibles no poseen una
distribución normal, pero se tiene que las varianzas son conocidas e
iguales a \(38.44\) y \(57.76\) para los motores \(A\) y \(B\)
respectivamente.
Solución
En este caso estamos interesados en calcular el límite inferior de un
intervalo de confianza del \(88\%\) para la diferencia promedio entre el
rendimiento de combustible en kilómetros por galón de gasolina que
ofrecen dos tipos de motores \(B\) y \(A\), tal que , \(\mu_B - \mu_A\),
y para calcular este límite inferior debemos revisar la información que
poseemos.
Del enunciado se menciona que los rendimientos de
combustible no poseen una distribución normal, pero se menciona que las
varianzas poblacionales son conocidas e iguales a \(\sigma^2_A=38.44\) y
\(\sigma^2_B=57.56\) para las maderas \(A\) y \(B\). En consecuencia,
tendremos que el intervalo de interés será el siguiente
y como estamos interesados en el límite inferior, el calculo que debemos
hacer tendrá la forma \[\begin{align*}
(\bar{X}_B-\bar{X}_A) - Z_{\alpha}\sqrt{\frac{\sigma^2_B}{n_B}+\frac{\sigma^2_A}{n_A}}
\end{align*}\]
Para realizar el cálculo del intervalo, se aprecia que requerimos de los
tamaños muestrales \(n_A=47\) y \(n_B=56\), las medias muestrales
\(\bar{X}_A=44\), y \(\bar{X}_B=48\), las varianzas poblacionales
\(\sigma^2_A=38.44\) y \(\sigma^2_B=57.56\), el nivel de confianza
\(1-\alpha=0.88\) y el valor crítico \(Z_{\alpha=0.12}=1.174987\). Al
reemplazar estos valores en el intervalo de interés obtenemos que
\[\begin{align*}
& (48-44) - 1.174987\sqrt{\frac{57.56}{56}+\frac{38.44}{47}} \\
& 4 - 1.174987(1.358576)\\
& 4 - 1.596309 \\
& 2.403691 < \mu_B - \mu_A
\end{align*}\]
y por tanto, se tendrá un con un nivel de confianza del \(88\%\), que el
límite inferior para la diferencia promedio entre los rendimiento de
combustible en kilómetro por galón de gasolina para los motores \(B\) y
\(A\) será de \(2.403691\) kilómetros.
Ejercicio
Suponga que se contrata a un grupo de investigación de la Universidad de
Antioquia para que realice un análisis de tensión sobre la unión pegada
con una resina experimental a dos clases diferentes de madera. Para
realizar el estudio, el grupo de investigación toma una muestra
aleatoria de \(18\) uniones pegadas con la resina especial a la madera
\(A\) y encontró que la tensión promedio de corte y desviación estándar
fueron de \(1130_{psi}\) y \(420_{psi}\), respectivamente. Por su parte,
toman una muestra aleatoria de \(12\) uniones pegadas con la resina
especial a la madera \(B\), encontrando que la tensión promedio de corte
y desviación estándar fueron de \(1010_{psi}\) y \(380_{psi}\).
Si se asume que la tensión sobre la unión pegada con la resina
experimental en cada clase de madera se distribuye aproximadamente
normal con varianzas diferentes. Construya un intervalo de confianza del
\(92\%\) para la diferencia de tensión promedio de corte para las dos
marcas de madera.
Solución
En este enunciado estamos interesados en construir un intervalo de
confianza del \(92\%\) para la diferencia entre los promedio a la
tensión sobre la unión pegada con una resina experimental para dos
clases de madera \(A\) y \(B\). En este caso, el intervalo de confianza
que se empleará será bilateral dado que no nos mencionan que se realice
el cálculo del límite superior o inferior para la diferencia. Para saber
cuál es el intervalo de interés, debemos revisar la información
calculada por el grupo de investigación.
De los datos
calculados por el grupo de investigación, encontramos que se realizó una
selección de \(18\) y \(12\) uniones para las maderas \(A\) y \(B\)
respectivamente, para las cuales se encontró de forma respectiva unas
medias muestrales de \(1130_{psi}\) y \(1010_{psi}\) junto a unas
desviaciones estándar de \(420_{psi}\) y \(380_{psi}\). Además, se
menciona de que las dos poblaciones se distribuyen de forma
aproximadamente normal con varianzas diferentes y en consecuencia se
tendrá el siguiente caso
y por tanto como el intervalo es bilateral, el calculo que debemos hacer
tendrá la forma \[\begin{align*}
(\bar{X}_A-\bar{X}_B) \pm t_{\frac{\alpha}{2}, \nu}\sqrt{\frac{S^2_A}{n_A}+\frac{S^2_B}{n_B}}
\end{align*}\]
En donde se observa que entre otros valores, requerimos calcular el
valor de los grados de libertad \(\nu\), tal que
\[\begin{align*}
\nu &= \frac{\left(\frac{S^2_A}{n_A} + \frac{S^2_B}{n_B}\right)^2}{\frac{(S^2_A/n_A)^2}{n_A-1} + \frac{(S^2_B/n_B)^2}{n_B-1}} \\
&= \frac{\left(\frac{420^2}{12} + \frac{380^2}{18}\right)^2}{\frac{(480^2/12)^2}{12-1} + \frac{(380^2/18)^2}{18-1}} \\
&= \frac{476694444}{18813149} \\
&= 25.33837
\end{align*}\]
Al calcular el valor techo de \(\nu\) tendremos que \[\begin{align*}
\nu &= 25.33837 \\
\lceil \nu \rceil &= \lceil25.33837\rceil \\
\lceil \nu \rceil &= 26
\end{align*}\]
y por tanto. se tendrá que los grados de libertad asociados a la
distribución \(t\) serán iguales a \(\nu= 26\). Ahora, los valores
adicionales que se requieren para realizar el cálculo del intervalo de
interés serán los tamaños muestrales \(n_A=12\) y \(n_B=18\), las medias
muestrales \(\bar{X}_A=1130\), y \(\bar{X}_B=1010\), las desviaciones
estándar muestrales \(S_A=420\) y \(S_B=380\), el nivel de confianza
\(1-\alpha=0.92\) y el valor crítico
\(t_{\frac{\alpha}{2}=0.04, \nu = 26}=1.821863\). Al reemplazar estos
valores en el intervalo de interés obtenemos que \[\begin{align*}
& (1130-1010) \pm 1.821863\sqrt{\frac{420^2}{12}+\frac{380^2}{18}} \\
& 120 \pm 1.821863(150.7389)\\
& 120 \pm 274.6256 \\
& -154.6256 < \mu_A - \mu_B < 394.6256
\end{align*}\]
De lo anterior, se concluye que con una confianza del \(92\%\), la
diferencia promedio entre la tensión promedio de corte entre las maderas
\(A\) y \(B\) se encontrará entre \(-154.6256_{psi}\) y
\(394.6256_{psi}\).
Ahora, como el intervalo es bilateral,
podemos verificar si existen o no diferencias significativas entre la
tensión promedio de corte de dos tipos de madera, y para ello debemos
verificar la posición en la que se encuentra el intervalo de confianza
para la diferencia entre \(\mu_A - \mu_B\).
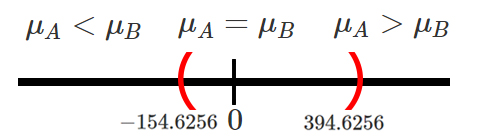En donde se observa que el intervalo calculado contiene el valor de
\(0\), el cual representa la igualdad entre la tensión promedio de corte
de dos tipos de madera, tal que \[\begin{align*}
\mu_A = \mu_B \quad =>\quad \mu_A - \mu_B = 0
\end{align*}\]
y por tanto, con un nivel de confianza del \(92\%\) no será posible
afirmar que existen diferencias significativas entre la tensión promedio
de corte de dos tipos de madera.
Intervalos de confianza para una proporción $p$
Sea $X_1,X_2, \ldots, X_n$ una muestra aleatoria iid de tamaño
$n$, tal que $X\sim b(n,p)$ entonces si $n$ es suficientemente
grande tal que $n\geq30$, y la proporción desconocida $p$ no se
encuentre cercana a $0$ o $1$, tal que $np>5$ y $n(1-p)>5$,
entonces un intervalo de confianza para la proporción $p$ es de la
forma 
Ejercicio
Suponga que se realiza un estudio sobre los costos que han tenido proyectos de renovación de parques en la ciudad de Medellín, encontrando que los costos asociados a \(20\) proyectos que se han llevado a cabo en la ciudad, en millones de pesos, fueron de
| 1780 | 2933 | 1220 | 1278 | 1170 | 1032 | 1245 | 2070 | 2040 | 1289 |
| 1531 | 980 | 1730 | 1380 | 2243 | 1687 | 1422 | 1731 | 1435 | 2080 |
Basados en la información anterior, construya un intervalo de confianza del \(97\%\) para la verdadera proporción de proyectos que poseen costos superiores a \(1900\) millones de pesos.
Solución
En este caso estamos interesados en el cálculo de un intervalo de
confianza del \(97\%\) para la proporción de proyectos que poseen costos
superiores a \(1900\) millones de pesos.
En donde, al no
mencionar un límite de confianza en particular se deberá realizar el
cálculo de un intervalo bilateral, el cual para el caso de una
proporción tiene la estructura
mostrando que el intervalo bilateral para el caso de una proporción está
dado por \[\begin{align*}
\hat{p} \pm Z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}
\end{align*}\]
En donde se observa que requerimos de la proporción muestral para
realizar el cálculo, y por tanto se deberá proceder a realizar su
cálculo, localizando en cuales valores muestrales se localiza un éxito,
el cual está dado por aquellos costos que posean un valor superior a
\(1900\) millones de pesos, y para ello, denotaremos como \(1\) aquellas
observaciones que sean superiores a \(1900\) millones de pesos, y \(0\)
aquellas observaciones que no cumplan la condición, tal que
\[\begin{align*}
\underset{0}{1780} \quad \underset{1}{2933} \quad \underset{0}{1220} \quad \underset{0}{1278} \quad \underset{0}{1170} \quad \underset{0}{1032} \quad \underset{0}{1245} \quad \underset{1}{2070} \quad \underset{1}{2040} \quad \underset{0}{1289} \\
\underset{0}{1531} \quad \underset{0}{980} \quad \underset{0}{1730} \quad \underset{0}{1380} \quad \underset{1}{2243} \quad \underset{0}{1687} \quad \underset{0}{1422} \quad \underset{0}{1731} \quad \underset{0}{1435} \quad \underset{1}{2080}
\end{align*}\] Al contar el número de éxitos, observamos que tenemos un
total de \(x=5\) éxitos en un total de \(n=20\) muestras, y por tanto,
podemos aplicar la fórmula de frecuencia relativa para calcular la
proporción muestral de egresados que poseen salarios superiores a
\(1900\) millones, tal que \[\begin{align*}
\hat{p} &= \frac{\text{# éxitos}}{\text{Total ensayos}} \\
&= \frac{x}{n} \\
&= \frac{5}{20} \\
&= 0.25
\end{align*}\]
Ahora, al emplear este valor junto con el nivel de confianza
\(1-\alpha=0.97\) y el valor crítico
\(Z_{\frac{\alpha}{2}=0.015}=2.17009\), para calcular el intervalo de
confianza de interés obtendremos que \[\begin{align*}
& 0.25 \pm 2.17009\sqrt{\frac{0.25(1-0.25)}{20}} \\
& 0.25 \pm 2.17009(0.09682458)\\
& 0.25 \pm 0.2101181 \\
& 0.0398819 < p < 0.4601181
\end{align*}\]
Por tanto, con una confianza del \(97\%\) se concluye que la verdadera
proporción de proyectos que poseen costos por encima de \(1900\)
millones de pesos, se encontrará entre \(3.99\%\) y \(46.01\%\).
Intervalos de confianza para diferencia de proporciones $p_1-p_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_2}$ dos muestras aleatorias iid de
tamaños $n_1$, y $n_2$, tal que $X_{1}\sim b(n,p)$ y
$X_{1}\sim b(n,p)$. Entonces si $n_1$ y $n_2$ son suficientemente
grandes tal que $n_1, n_2 \geq30$, y las proporciones desconocidas
$p_1$ y $p_2$ no se encuentran cercanas a $0$ o $1$, tal que
$n_1p_1>5$, $n_2p_2>5$, $n_1(1-p_1)>5$ y $n_2(1-p_2)>5$,
entonces un intervalo de confianza para la diferencia de proporciones
$p_1-p_2$ es de la forma
Ejercicio
Una empresa de computación decide realizar un cambio en el proceso de
fabricación de uno de los componentes que requiere en sus portátiles, y
está en interesado en saber si dicho cambio ofrece una mejora
significativa en la rendimiento que sus equipos ofrecen.
Para
determinar si el cambio en el proceso de fabricación mejora el
rendimiento que sus equipos ofrecen, deciden tomar una muestra de
equipos antes y después de la implementación del nuevo proceso de
fabricación y se evalúa la velocidad de procesamiento para la ejecución
de un programa determinado. Suponga que se encuentra que \(120\) de
\(500\) computadores fabricados con el método actual ofrece un
rendimiento superior al promedio, mientras que, \(220\) de \(700\)
computadores fabricados con el nuevo método ofrece un rendimiento
superior al promedio.
Basados en la información obtenida,
calcule un intervalo de confianza del \(99\%\) para la verdadera
diferencia entre las proporciones de equipos que ofrecen un rendimiento
superior al promedio entre el proceso de fabricación actual y el nuevo.
Es posible pensar que el nuevo proceso si mejora el rendimiento promedio
de los equipos de cómputo?
Solución
En este enunciado estamos interesados en construir un intervalo de
confianza del \(99\%\) para la diferencia entre la proporción de equipos
que son fabricados mediante un proceso de fabricación nuevo y aquellos
que son fabricados con un proceso de fabricación actual, en donde, se
debe construir un intervalo de confianza bilateral debido a que no nos
preguntan por un límite en específico.
Para llevar a cabo el
cálculo debemos revisar la información que poseemos. En primer lugar
observamos que nos hablan de los tamaños de muestra para cada una de las
poblaciones en donde el tamaño de muestra para los equipos fabricados
mediante el proceso de fabricación nuevo fue de \(n_N= 500\), mientras
que, el tamaño de muestra para lo equipos fabricados mediante el proceso
de fabricación actual es de \(n_A=700\).
Adicionalmente, se
presenta para cada valor de la muestra, el número de equipos que
ofrecieron una velocidad de procesamiento superior al promedio, siendo
dichos valores para los equipos fabricados con el proceso nuevo y actual
\(x_N=120\) y \(x_A=220\), respectivamente. Con estos valores es posible
realizar el cálculo de las proporciones muestrales para las dos
poblaciones, tal que para el caso de los equipos que fueron construidos
con el nuevo procedimiento tenemos que \[\begin{align*}
\hat{p}_N &= \frac{\text{# de equipos nuevos con rendimiento superior}}{\text{Total equipos nuevos evaluados}} \\
&= \frac{x_N}{n_N} \\
&= \frac{220}{700} \\
&= 0.3142857
\end{align*}\] mientras que, para los equipos que fueron construidos con
el procedimiento actual tenemos que \[\begin{align*}
\hat{p}_A &= \frac{\text{# de equipos actuales con rendimiento superior}}{\text{Total equipos actuales evaluados}} \\
&= \frac{x_A}{n_A} \\
&= \frac{120}{500} \\
&= 0.24
\end{align*}\] Ahora, dado que el intervalo que nos piden es bilateral,
y tenemos que los tamaños muestrales para cada población son
suficientemente grandes, tendremos que el intervalo de interés es de la
forma
y por tanto como el intervalo de interés es de la forma, el calculo que
debemos hacer tendrá la forma \[\begin{align*}
(\hat{p}_N-\hat{p}_A) \pm Z_{\alpha}\sqrt{\frac{\hat{p}_N(1-\hat{p}_N)}{n_N}+\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}}
\end{align*}\]
En donde se observa que entre los valores ya calculados para las
proporciones muestrales, se requiere del nivel de confianza
\(1-\alpha=0.99\) y el valor crítico \(Z_{\alpha=0.01}=2.326348\). Al
reemplazar estos valores en el intervalo de interés obtenemos que
\[\begin{align*}
& (0.3142857-0.24) \pm 2.326348\sqrt{\frac{0.3142857(1-0.3142857)}{700}+\frac{0.24(1-0.24)}{500}} \\
&0.0742857 \pm 2.326348 (0.02593592) \\
&0.0742857 \pm 0.06033598 \\
&0.01394972 < p_N - p_A < 0.1346217
\end{align*}\]
Dado el resultado anterior, se concluye con una confianza del del
\(99\%\) que la diferencia entre la proporción de equipos que son
fabricados mediante un proceso de fabricación nuevo y aquellos que son
fabricados con un proceso de fabricación actual se encontrará entre
\(1.39\%\) y \(13.46\%\).
Ahora, como el intervalo es
bilateral, podemos verificar si existen o no diferencias significativas
entre la proporción de equipos que son fabricados mediante el nuevo
proceso de fabricación y aquellos que son fabricados mediante el proceso
actual, y para ello debemos verificar la posición en la que se encuentra
el intervalo de confianza para la diferencia entre \(p_N - p_A\).
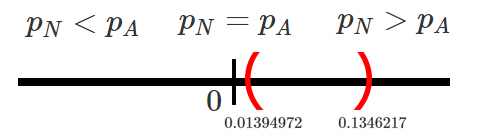En donde se observa que el intervalo calculado se encuentra sobre el
valor de \(0\), el cual representa la igualdad entre las dos
proporciones, tal que \[\begin{align*}
p_N = p_A \quad =>\quad p_N - p_A = 0
\end{align*}\]
y por tanto, podremos afirmar con un nivel de confianza del \(99\%\) que
la proporción de equipos que ofrece un rendimiento superior al promedio
y son fabricados mediante el nuevo proceso, es superior a la proporción
de aquellos fabricados mediante el proceso actual.
Intervalos de confianza para una varianza $\sigma^2$
Sea $X_{1}, X_{2}, \ldots, X_{n}$ una muestra aleatoria de una
problación normal de tamaño $n$ conmedias $\mathbb{E}(X)=\mu$ y
varianza desconocidas $Var(X)=\sigma_1^2<\infty$, entonces un
intervalo de confianza del $100(1-\alpha)\%$ para la varianza
desconocida $\sigma^2$ estará dada por
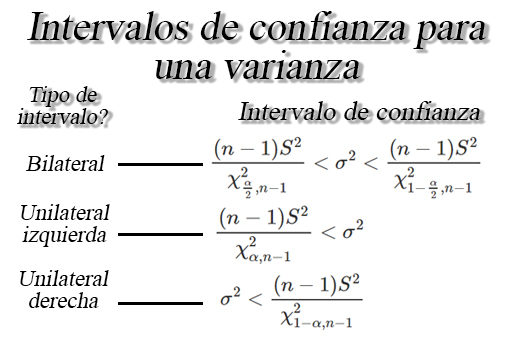
Ejercicio
Suponga que se realiza un estudio sobre los costos que han tenido proyectos de renovación de parques en la ciudad de Medellín, encontrando que los costos asociados a \(20\) proyectos que se han a cabo en le ciudad, en millones de pesos, fueron de
| 1780 | 2933 | 1220 | 1278 | 1170 | 1032 | 1245 | 2070 | 2040 | 1289 |
| 1531 | 980 | 1730 | 1380 | 2243 | 1687 | 1422 | 1731 | 1435 | 2080 |
Si es posible supone que el costo de construir cualquier parque se distribuyen aproximadamente normal, calcule un intervalo de confianza para la variabilidad de los costos de construir cualquier parque, empleando un nivel de confianza del \(95\%\).
Solución
En este punto nos mencionan que se tiene interés en calcular un
intervalo de confianza para la variabilidad de los costos de construir
cualquier parque. En donde al no mencionar si se está interesado en el
límite superior o inferior, se tendrá que el intervalo será bilateral,
tal que
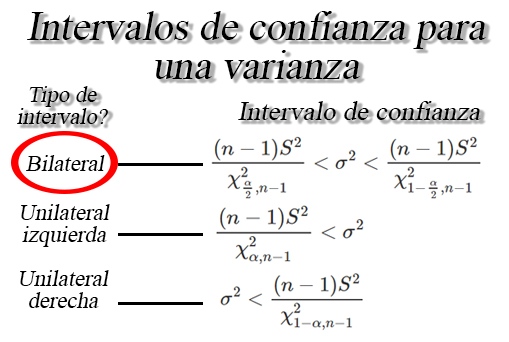en donde se aprecia que el intervalo bilateral para una varianza posee
la estructura \[\begin{align*}
\frac{(n-1)S^2}{\chi^2_{\frac{\alpha}{2}, n-1}}< \sigma^2 <\frac{(n-1)S^2}{\chi^2_{1 -\frac{\alpha}{2}, n-1}}
\end{align*}\]
En donde se observa que para realizar el cálculo del intervalo, se
requiere de la varianza muestral \(S^2 = 230541.2\), el nivel de
confianza \(1-\alpha=0.95\), los valores críticos
\(\chi^2_{\frac{\alpha}{2}=0.025, n-1=19}=32.85233\) y
\(\chi^2_{1-\frac{\alpha}{2}=0.975, n-1=19}=8.906516\) y el tamaño
muestral \(n=20\).
Al reemplazar dichos valores en el
intervalo de confianza, se tendrá que \[\begin{align*}
\frac{(n-1)S^2}{\chi^2_{\frac{\alpha}{2}, n-1}} &< \sigma^2 <\frac{(n-1)S^2}{\chi^2_{1 -\frac{\alpha}{2}, n-1}} \\
\frac{(20-1)230541.2}{32.85233}&< \sigma^2 <\frac{(20-1)230541.2}{8.906516} \\
133332.5 &< \sigma^2 < 491806.5
\end{align*}\]
Lo cual significa que la desviación estándar estará entre
\[\begin{align*}
133332.5 &< \sigma^2 < 491806.5\\
\sqrt{133332.5} &< \sqrt{\sigma^2} < \sqrt{491806.5}\\
365.1472 &< \sigma < 701.2892\\
\end{align*}\]
De lo anterior, se podrá concluir con un nivel de confianza del \(95\%\)
que el verdadero valor para la desviación estándar de los costos de
construcción de cualquier parque estará entre \(365.1472\) y
\(701.2892\) millones de pesos.
Intervalos de confianza para razón de varianzas $\sigma^2_1/\sigma^2_2$
Sea $X_{1,1}, X_{1,2}, \ldots, X_{1,n_1}$ y
$X_{2,1}, X_{2,2}, \ldots, X_{2,n_1}$ dos muestras aleatorias normales
de tamaños $n_1$, y $n_2$ con medias $\mathbb{E}(X_{1})=\mu_1$ y
$\mathbb{E}(X_{2})=\mu_2$, y varianzas desconocidas
$Var(X_{1})=\sigma_1^2<\infty$ y $Var(X_{2})=\sigma^2_2<\infty$,
respectivamente, entonces un intervalo de confianza del
$100(1-\alpha)\%$ para $\sigma^2_1/\sigma^2_2$ estará dada por
Ejercicio
Se aplican pruebas a \(10\) cables conductores soldados a un dispositivo semiconductor con el fin de determinar su resistencia a la tracción. Las pruebas demostraron que para romper la unión se requiere las libras de fuerza que se listan a continuación.
| Sin Encapsulado | 19.8 | 12.7 | 13.2 | 16.9 | 10.6 | 18.8 | 11.1 | 14.3 | 17.0 | 12.5 |
Otra conjunto de \(8\) cables conductores que forman otro dispositivo, se encapsulan y se prueban para determinar si el encapsulado aumenta la resistencia a la tracción, obteniendo para este caso se requirieron las siguientes libras de fuerza para romper la unión
| Con Encapsulado | 24.9 | 22.9 | 23.6 | 22.1 | 20.3 | 21.6 | 21.9 | 22.5 |
Si se supone que las resistencias a la tracción se distribuyen normalmente, construya un intervalo del \(90\%\) para la razón de varianzas entre la variabilidad de los cables sin encapsulado y la variabilidad de los cables con encapsulado. Es posible afirmar que la variabilidad de de los cables con encapsulado es superior a los cables sin encapsulado?
Solución
En este punto nos mencionan que se tiene interés en calcular un
intervalo de confianza para el cociente de las varianzas asociadas a la
resistencia a la tracción para cables sin encapsulado y cables con
encapsulado. Además nos mencionan que la resistencia a la tracción hasta
la ruptura se distribuye normalmente, y por tanto deberemos calcular el
siguiente intervalo
en donde se aprecia que el intervalo bilateral para la razón de
varianzas posee la estructura \[\begin{align*}
\frac{S^2_C}{S^2_S}\frac{1}{f_{\alpha/2, n_C-1, n_S-1}} < \frac{\sigma^2_C}{\sigma^2_S} < \frac{S^2_C}{S^2_S}f_{\alpha/2, n_S-1, n_C-1}
\end{align*}\]
En donde se observa que para realizar el cálculo del intervalo, se
requiere de los varianzas muestrales \(S^2_S\) y \(S^2_C\), el nivel de
confianza \(1-\alpha\) y los valores críticos
\(f_{\alpha/2, n_C-1, n_S-1}\) y \(f_{\alpha/2, n_S-1, n_C-1}\).
Para realizar el cálculo de las varianzas muestrales, se emplean
los datos muestrales y los tamaños de muestra \(n_C=8\) y \(n_S=10\),
tal que al realizar el cálculo obtenemos
\[\begin{align*}
S^2_C = 1.378146 \quad \text{ y } \quad S^2_S = 3.231254
\end{align*}\]
Por su parte, al buscar los valores críticos para un nivel de
significancia \(1-\alpha=0.90\) y tamaños muestrales \(n_C=8\) y
\(n_S=10\) tenemos que
\[\begin{align*}
f_{\alpha/2 = 0.05, n_C-1 = 7, n_S-1 = 9} = 3.292746\\
f_{\alpha/2 = 0.05, n_S-1 = 9, n_C-1 = 7} = 3.676675
\end{align*}\]
Una vez calculados los valores necesarios para calcular el intervalo de
confianza, se procede a su cálculo, tal que \[\begin{align*}
\frac{1.378146}{3.231254}\frac{1}{3.292746} &< \frac{\sigma^2_C}{\sigma^2_S} < \frac{1.378146}{3.231254}3.676675 \\
0.1295287 &< \frac{\sigma^2_C}{\sigma^2_S} < 1.56812
\end{align*}\]
Por tanto, se podrá concluir con un nivel de confianza del \(90\%\) que
el verdadero valor para el cociente de varianzas entre la variabilidad
de los cables sin encapsulado y la variabilidad de los cables con
encapsulado, se encontrará entre \(0.1295287\) y \(1.56812\).
Ahora, para verificar si existen o no diferencias significativas entre
las varianzas de resistencia a la tracción de los cables encapsulados o
sin encapsular, debemos verificar la posición en la que se encuentra el
intervalo de confianza para la razón de varianzas
\(\sigma^2_C/\sigma^2_S\).
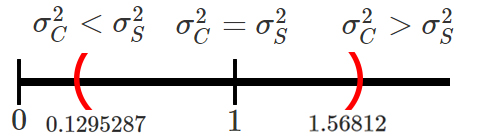En donde se observa que el intervalo calculado contiene el valor de
\(1\), el cual representa la igualdad entre la varianza de los dos tipos
de cable, tal que \[\begin{align*}
\sigma^2_C = \sigma^2_S \quad =>\quad \frac{\sigma^2_C}{\sigma^2_S} = 1
\end{align*}\]
y por tanto, con un nivel de confianza del \(90\%\) no será posible
afirmar que la variabilidad de la resistencia a la tracción de los
cables encapsulados o sin encapsular sean diferentes, y por tanto, debe
asumirse que éstos son iguales.
Análisis de Regresión
El análisis de regresión es una técnica estadística que se emplea para investigar y modelar la relación existente entre variables.
Existen numerosas aplicaciones del análisis de regresión, las cuales se dan en casi cualquier campo de estudio como lo es en ingeniería, economía, biología, medicina, ciencias sociales, entre otras, y por tanto puede ser considerada como la técnica estadística más usada en la práctica.
Para entender este tipo de relación, se suponen inicialmente dos
variables, la primera variable será la variable $Y$ la cual es
variable dependiente o variable respuesta, mientras que la segunda
variable será la variable $X$ la cual es la variable independiente o
variable explicativa.
El objetivo será estudiar la relación asociada entre $Y$ y $X$ (la
cual no es necesariamente de causa-efecto), y para ello miraremos los
siguientes casos de estudio.
-
Caso 1 (Diseño experimental controlado): Se realiza un
estudio en un supermercado para observar la relación existente entre el
espacio asignado para la exhibición de licores y las ventas semanales de
licores que se realizan. Suponga que durante \(15\) semanas se decide
distribuir de forma aleatoria el espacio disponible para la exhibición,
usando como referencia el número de estanterías iguales a \(3\), \(5\) y
\(7\). Los resultados para las \(15\) semanas se registran a
continuación.
Espacio asignado Ventas semanales 3 491 7 534 3 495 3 500 5 496 7 527 5 491 3 476 5 512 5 492 7 546 7 532 5 492 3 461 7 529 -
Interés - Objetivos
- Investigar la relación existente entre las ventas semanales y el espacio asignado.
- Determinar si hay una relación significativa entre el espacio asignado a los licores y las ventas semanales.
- Hacer la estimación de las ventas semanales cuando se asigna un espacio para exhibición de licor de \(7\) estanterías.
- Predecir el valor de las ventas semanales si para la semana siguiente se asigna un espacio de \(4\) estanterías para exhibir licor.
-
Caso 2 (Mediciones Repetidas): Un estudiante de gestión
socioeconómica de proyectos quiere observar si hay una relación entre el
gasto en campañas publicitarias y las donaciones recibidas para la
construcción de parques y bibliotecas para sectores de la población con
bajos recursos. Para realizar el estudio se toma como referencia \(10\)
meses en los cuales hicieron gastos en publicidad y obtuvieron los
siguientes datos en millones de pesos
Gasto en Publicidad Donaciones recibidas 40 385 20 400 25 395 20 365 30 475 50 440 40 490 20 420 50 560 40 525 -
Interés - Objetivos
- Investigar la relación existente entre las ventas semanales y el espacio asignado.
- Ajustar un modelo que permita explicar las donaciones recibidas en función del gasto en publicidad.
- Predecir el valor de las donaciones realizadas en caso de gastar en publicidad \(53\) millones de pesos.
-
Caso 3 (Datos Históricos): Un perito desea determinar
si existe alguna relación entre el costo de una propiedad y el valor
registrado en el predial. Para ello selecciona \(10\) propiedades de una
base de datos y registra el valor de la propiedad para verificar el
valor registrado en el predial obteniendo los siguientes resultados en
millones de pesos
Costo propiedad Valor predial 214.199 112.361 284.061 238.541 239.673 159.144 269.327 212.431 192.689 74.433 250.846 178.492 260.795 196.032 246.879 172.886 238.412 156.830 223.949 191.174 -
Interés - Objetivos
- Ajustar un modelo de regresión que explique el valor comercial de la propiedad en función del valor del predial
- Predecir el valor de una propiedad cuyo valor en el predial es de \(180\) millones de pesos.
Regresión Lineal Simple
Si se supone que la relación entre $Y$ y $X$ es lineal, un modelo
adecuado estaría dado por
\begin{align*} Y=\beta_0 + \beta_1 X+ \varepsilon \quad \quad (I) \end{align*}
donde
$\beta_0$y$\beta_1$: son dos constantes desconocidas denominadas parámetros del modelo, estimados a partir de los datos.$\beta_0$representa el intercepto.$\beta_1$representa la pendiente.$\varepsilon$representa al componente de error aleatorio denominado error estadístico, el cual explica por qué el modelo de regresión lineal simple no ajusta exactamente los datos.
Nota: Es de anotar que el término de error $\varepsilon$ contiene
todos los efectos de otras variables que no fueron consideradas en el
modelo, errores de medición u otras consideraciones no tenidas en cuenta
por el investigador.
Supuestos del modelo de regresión lineal simple
- Se tiene una muestra aleatoria de
$n$parejas$(y_1, x_1), (y_2, x_2), \ldots, (y_n, x_n)$, en donde el objetivo principal del análisis de regresión es encontrar la recta que mejor ajuste a los pares de observaciones, y por tanto se supone que las parejas satisfacen el modelo$(I)$, tal que\begin{align*} y_i=\beta_0 + \beta_1 x_i+ \varepsilon_i \quad \text{ para } i =0,1,2, \ldots, n \quad \quad (II) \end{align*}donde$y_i$es la i-ésima observación de la variable$Y$, dado que$X$es igual a$x_i$. - Del modelo
$(II)$suponga que las$\varepsilon_i$son variables aleatorias independientes con media$\mathbb{E}(\varepsilon_i)=0$y varianza$Var(\varepsilon_i)=\sigma^2$, de tal forma que\begin{align*} \mathbb{E}(y_i)=\beta_0 + \beta_1 x_i+ \mathbb{E}(\varepsilon_i) = \beta_0 + \beta_1 x_i \end{align*}y\begin{align*} Var(y_i)=Var(\varepsilon_i) = \sigma^2 \end{align*}en donde, si además se cumple que$\varepsilon_i\sim N(0,\sigma^2)$, entonces se tendrá que\begin{align*} y_i\sim N(\beta_0+\beta_1x_i, \sigma^2) \end{align*}
Estimación de parámetros
El objetivo de un modelo de regresión será entonces estimar los
parámetros $\beta_0, \beta_1, \sigma^2$ del modelo lineal, y para ello
puede recurrirse a diferentes métodos, entre los cuales destaca el
método de Máxima Verosimilitud y el método de mínimos cuadrados.
Método de Máxima Verosimiliud
Bajo el supuesto de que
$\varepsilon \stackrel{iid}{\sim} N(0,\sigma^2)$, entonces
$y_i|x_i \stackrel{iid}{\sim} N(\beta_0 + \beta_1 x_i, \sigma^2)$,
luego la función de verosimilitud asociada a los pares $(y_1, x_1)$,
$(y_2, x_2)$, $\ldots$, $ (y_n,x_n)$ está dada por
\begin{align*} L(\beta_0, \beta_1, \sigma^2; (y_i, x_i)) &= \prod_{i=1}^n f(y_i; \beta_0, \beta_1, \sigma^2)\\ &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi}\sqrt{\sigma^2}}e^{-\frac{1}{2}\frac{(y_i - \beta_0 - \beta_1 x_i)^2}{\sigma^2}} \end{align*}
Entonces, al maximizar la función de probabilidad tal como se enseño en
la
Clase
08 se encontrará que los estimadores de $\beta_0$, $\beta_1$ y
$\sigma^2$ que maximizan $L(\cdot)$ están dados por
\begin{align*} \hat{\beta}_0&=\bar{Y} - \hat{\beta}_1\bar{X}\\ \hat{\beta}_1&=\frac{S_{xy}}{S_{xx}}= \frac{\sum_{i=1}^n (x_i - \bar{X})(y_i - \bar{Y})}{\sum_{i=1}^{n}(x_i - \bar{X})^2} = \frac{\sum_{i=1}^{n}(x_i-\bar{X}) y_i}{\sum_{i=1}^{n} (x_i - \bar{X})^2}\\ \hat{\sigma}^2&= \frac{\sum_{i=1}^{n} (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)^2}{n} \end{align*}
Método de Mínimos Cuadrados
Sea una muestra aleatoria $(y_1, x_1), (y_2, x_2), \ldots, (y_n, x_n)$
a partir de la cual se desea ajustar el siguiente modelo
\begin{align*} y_i=\beta_0 + \beta_1 x_i+ \varepsilon_i \end{align*}
donde $\varepsilon_i$ es una variable aleatoria desconocida con
distribución de probabilidad independiente e idénticamente distribuida
con media $\mathbb{E}(\varepsilon_i)=0$ y varianza
$Var(\varepsilon_i)=\sigma^2$.
Entonces si denotamos a $\hat{\beta}_0, \hat{\beta}_1$, los
estimadores de los parámetros $\beta_0, \beta_1$, entonces la recta de
regresión estimada será
\begin{align*} \hat{y_i}=\hat{\beta}_0 + \hat{\beta}_1 x_i \end{align*}
donde $\hat{y}_i$ es el estimador de $\mathbb{E}(y_i|x=x_i)$.
Entonces la diferencia entre $y_i$ y $\hat{y_i}$ se conoce como
error de estimación del ajuste $e_i$ y está dado por
\begin{align*} e_i = y_i - \hat{y}_i = y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i \end{align*}
Supuestos
$e_i\sim N(0,\sigma^2_e)$, varianza constante (homocedasticidad)$cov(e_i. e_j)=0$para todo$i \neq j$.
A partir de la ecuación anterior será posible encontrar los estimadores
$\hat{\beta}_0$ y $\hat{\beta}_1$ mediante la minimización de la
suma de los cuadrados de los errores.
\begin{align*} SCE=\sum_{i=1}^n e_i^2 = \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \sum_{i=1}^n (y_i -\hat{\beta}_0 - \hat{\beta}_1 x_i)^2 \end{align*}
de la forma
\begin{align*} \frac{\partial SCE}{\partial \hat{\beta}_i} = 0 \end{align*}
Al resolver el sistema de ecuaciones se obtendrá que
\begin{align*} \hat{\beta}_1 &= \frac{\sum_{i=1}^n (x_i-\bar{X})(y_i-\bar{Y})}{\sum_{i=1}^n (x_i-\bar{X})^2} = \frac{S_{xy}}{S_{xx}}\\ \hat{\beta}_0 &= \bar{Y} - \hat{\beta}_1\bar{X} \end{align*}
Note que
- Los EMV para
$\beta_0$y$\beta_1$coinciden con los estimadores de mínimos cuadrados. - Observe que
$\hat{\beta}_0$y$\hat{\beta}_1$pueden ser reescritos como
\begin{align*} \hat{\beta}_1 &= \sum_{i=1}^{n} y_ic_i \qquad \text{ donde } c_i=\frac{(x_i-\bar{X})}{\sum_{i=1}^{n}(x_i - \bar{X})^2}\\ \hat{\beta}_0 &= \sum_{i=1}^{n} y_i di \qquad \text{ donde } d_i=\left(\frac{1}{n} - c_i\bar{X}\right) \end{align*}
Además, se puede probar que
$\sum_{i=1}^{n}c_i=0$$\sum_{i=1}^{n}d_i=1$$\sum_{i=1}^{n}c_ix_i=1$$\sum_{i=1}^{n}d_ix_i=0$$\sum_{i=1}^{n}c_i^2=\frac{1}{\sum_{i=1}^{n} (x_i-\bar{X})^2} = \frac{1}{S_{xx}}$$\sum_{i=1}^{n}d_i^2=\frac{\sum_{i=1}^{n}x_i^2}{n\sum_{i=1}^{n} (x_i-\bar{X})^2} = \frac{\sum_{i=1}^{n}x_i^2}{nS_{xx}}$
Propiedades de $\hat{\beta}_0, \hat{\beta}_1$
A continuación se presentan algunas propiedades que cumplen los
estimadores de los parámetros $\hat{\beta}_0, \hat{\beta}_1$. La
demostración corre por cuenta del estudiante.
$\mathbb{E}(\hat{\beta}_0) = \beta_0$$\mathbb{E}(\hat{\beta}_1) = \beta_1$$Var(\hat{\beta}_0) = \sigma^2 \left[\frac{1}{n} + \frac{\bar{X}^2}{S_{xx}}\right]$$Var(\hat{\beta}_1) = \frac{1}{S_{xx}}\sigma^2$
Nota
Dado que el método de mínimos cuadrados no posee un estimador para la
varianza $\sigma^2$, se emplea entonces un estimador insesgado el cual
estará dado por
\begin{align*} \sigma^2_e &=\frac{1}{n-2}\sum_{i=1}^n e^2_i \\ &= \frac{1}{n-2}\sum_{i=1}^n (y_i - \hat{y}_i)^2 \\ &= \frac{S_{yy} - \hat{\beta}_1 S_{xy}}{n-2} \end{align*}
Prueba de hipótesis
Note que $\hat{\beta}_0$ y $\hat{\beta}_1$ son combinaciones
lineales de $y_i$, que son normales e independientes, entonces por
propiedades de la distribución normal se obtiene que
\begin{align*} \hat{\beta}_0 &\sim N\left(\beta_0, \left[\frac{1}{n} + \frac{\bar{X}^2}{S_{xx}}\right]\sigma^2_e\right) \\ \hat{\beta}_1 &\sim N\left(\beta_1, \frac{\sigma^2_e}{S_{xx}}\right) \end{align*}
Entonces, para realizar el contraste de hipótesis $\beta_0$ y
$\beta_1$ de la forma
\begin{align*} H_0: \beta_0 = \beta_{00} \quad & \quad H_0: \beta_1 = \beta_{10}\\ H_1: \beta_0 \neq \beta_{00} \quad & \quad H_1: \beta_1 \neq \beta_{10}\\ \end{align*}
se tendrá que los estadísticos de prueba serían de la forma
\begin{align*} t_{\hat{\beta}_{0}}= \frac{\hat{\beta}_0 - \beta_{00}}{\sqrt{\left[\frac{1}{n} + \frac{\bar{X}^2}{S_{xx}}\right]\sigma^2_e}} \quad & \quad t_{\hat{\beta}_{1}}= \frac{\hat{\beta}_1 - \beta_{10}}{\sqrt{\frac{\sigma^2_e}{S_{xx}}}} \end{align*}
y para tomar la decisión si se rechaza o no la hipótesis se emplean la
región crítica la cual está dada por
\begin{align*} RC:\{t|t < -t_{\frac{\alpha}{2}, n-2} \quad ó \quad t > t_{\frac{\alpha}{2}, n-2}\} \end{align*}
en donde si $t_{\hat{\beta}_{i}} \in RC$ para $i=0,1$, se rechaza
$H_0$. Mientras que el P-valor está dada por
\begin{align*} \text{P-valor}= 2\mathbb{P}(t_{n-2}\geq |t_{\hat{\beta}_i}|) \quad \text{ para } i = 0,1 \end{align*}
en donde si P-valor es menor al nivel de significancia $\alpha$,
entonces se rechaza $H_0$.
Nota
- Usualmente se quiere probar si
$\beta_{0}=0$y$\beta_{1}=0$, ya que se quiere probar a significancia de los parámetros. - Observe que rechazar
$H_0:\beta_{1}=0$, en la prueba de significancia, permite afirmar que la relación entre las variables$Y$y$X$se pueden aproximar mediante una linea recta. - Si no se rechaza
$H_0:\beta_{1}=0$, significa que independiente del valor de$X$, el valor de$Y$será el mismo, y por tanto, no habrá una relación lineal entre$Y$y$X$.
Intervalo de confianza
El intervalo de confianza par $\beta_0$ está dado por
\begin{align*} \hat{\beta}_0 - t_{\frac{\alpha}{2}, n-2} \sqrt{\left(\frac{1}{n}+\frac{\bar{X}^2}{S_{xx}}\right)\sigma^2_{e}} < \beta_0 < \hat{\beta}_0 + t_{\frac{\alpha}{2}, n-2} \sqrt{\left(\frac{1}{n}+\frac{\bar{X}^2}{S_{xx}}\right)\sigma^2_{e}} \end{align*}
para el caso de $\beta_1$, el intervalo de confianza está dado por
\begin{align*} \hat{\beta}_1 - t_{\frac{\alpha}{2}, n-2} \sqrt{\frac{\sigma^2_{e}}{S_{xx}}} < \beta_1 < \hat{\beta}_1 + t_{\frac{\alpha}{2}, n-2} \sqrt{\frac{\sigma^2_{e}}{S_{xx}}} \end{align*}
Nota
Si el Intervalo de Confianza de $\beta_1$ no contiene el cero, se
puede afirmar que la variable $Y$ está relacionada linealmente con la
variable independiente $X$. En caso contrario, no existe relación
lineal entre $X$ y $Y$, es decir, la variable $X$ no es adecuada
para predecir el comportamiento de $Y$.
Analisis de varianza
Una forma equivalente de hacer la prueba de significancia de la
regresión $H_0:\beta_1=0$ vs $H_1:\beta_1\neq0$ es a partir del
análisis de varianza, donde se descompone la varianza total de $Y$
($SCT$) en dos fuentes, la variabilidad explicada por el modelo
($SCR$) y la variabilidad no explicada por el modelo ($SCE$).
$SCT = \sum_{i=1}^n (y_i-\bar{Y})^2$$SCR = \sum_{i=1}^n (\hat{y}_i-\bar{Y})^2$$SCE = \sum_{i=1}^n (y_i-\hat{y}_i)^2$
Observe que las diferencias de las $y_i$ con a su media $\bar{Y}$
pueden escribirse como
\begin{align*} (y_i - \bar{Y}) = (\hat{y}_i - \bar{Y}) + (\underbrace{y_i - \hat{y_i}}_{e_i}) \end{align*}
lo cual puede reescribirse como
\begin{align*} SCT = SCR + SCE \end{align*}
al aplicar la función de sumatoria a ambos lados de la función.
Nota
a)Para llegar a la ecuación anterior se puede verificar que
\begin{align*} \sum_{i=1}^{n}(\hat{y}_i - \bar{Y})e_i = \sum_{i=1}^{n}(\hat{y}_i - \bar{Y}) (y_i - \hat{y_i}) \end{align*}
b)La expresiones de $SCT$, $SCR$ y $SCE$ pueden ser reescritas
como
\begin{align*} &SST = \sum_{i=1}^{n}y_i^2 - n\bar{Y}\\ &SSR = \hat{\beta}_1S_{xy} = \hat{\beta}_1^2 S_{xx}\\ &\text{y luego se podrá calcular }SCE \text{ como}\\ &SCE = SST - SSR \end{align*}
c)Cada suma de cuadrados tiene asociado un número de grados de libertad
diferentes, tal que
\begin{align*} \underbrace{SCT}_{n-1} = \underbrace{SCR}_{1} + \underbrace{SCE}_{n-2} \end{align*}
con base en lo anterior es posible construir estimadores independientes
de $\sigma^2$, usando la respectiva suma de cuadrados dividido sus
grados de libertad, tal que
\begin{align*} MSR = \frac{SCR}{1} \quad \quad MSE = \frac{SCE}{n-2} \end{align*}
finalmente se establece el estadítico de prueba bajo el supuesto de
normalidad
\begin{align*} F_c= \frac{SCR / 1}{SCE / n-2} \sim F_{1, n-2} \end{align*}
En donde el criterio de decisión estará dado, la región crítica, la cual
estará dada por
\begin{align*} RC:\{F|F>F_{\alpha, 1, n-2}\} \end{align*}
o el P-valor, el cual estará dado por
\begin{align*} \text{P-valor} = \mathbb{P}(F_{1,n-2} > F_c) \end{align*}
donde si P-valor es menor al nivel de significancia $\alpha$ se
rechaza la hipótesis nula y se concluye que el modelo lineal propuesto
es significativo para explicar el comportamiento $Y$.
Coeficiente de determinación
Una forma de medir la bondad del ajuste del modelo de regresión es
mediante el coeficiente de determinación $R^2$, el cual se define como
\begin{align*} R^2=\frac{SCR}{SCT} = 1 - \frac{SCE}{SCT} \end{align*}
y representa la proporción de variación total de $Y$, explicada por su
relación lineal con $X$.
Dado que $R^2$ se encuentra entre $0$ y $1$, entonces valores
cercanos a cero indican que la relación entre $X$ y $Y$ es muy
pobre, mientras que, valores cercanos a uno, indican que la recta
ajustada se aproxima relativamente bien a los puntos.
Nota: Un $R^2$ alto no garantiza necesariamente que el modelo
regresión lineal ajustado sea adecuado para los datos, debido que hay
factores que afectan a este valor, como lo es el número de datos usados.
Respuesta media y predicción de nuevas observaciones
Una importante utilidad del modelo de regresión es que nos permite la
estimación de la media de la distribución de $Y$ para un valor dado de
$X$, y además nos permite realizar predicciones sobre una nueva
variable $y_0$ correspondiente a un nivel especificado de variables
$x_0$.
Respuesta media
Considere un valor determinado $x = x_0$, y el objetivo será estimar
su respuesta media $\mathbb{E}(Y|x_0)$. La estimación puede ser
puntual o por intervalo, y donde, la estimación es válida solo para
valores de $x_0$ dentro del rango de valores originales de $X$, que
se usaron para ajustar el modelo.
Entonces el estimador puntual de la respuesta media de $Y$ dado
$x_0$
\begin{align*} \hat{y_0}= \hat{\mathbb{E}}(Y|x_0)= \hat{\beta}_0 + \hat{\beta}_1 x_0 \end{align*}
donde se puede probar que
\begin{align*} \mathbb{E}(\hat{y_0}) &= \beta_0 + \beta_1 x_0 \\ Var(\hat{y_0}) &= \hat{\sigma}^2_e\left[\frac{1}{n} + \frac{(x_0 - \bar{X})^2}{S_{xx}}\right] \end{align*}
Además, para un nivel de confianza del $100(1-\alpha)\%$ un intervalo
de confianza para la respuesta media será de la forma
\begin{align*} \hat{y}_0 \pm t_{\frac{\alpha}{2}, n-2} \sqrt{\hat{\sigma}^2_e\left[\frac{1}{n}+ \frac{(x_0 - \bar{X})^2}{S_{xx}}\right]} \end{align*}
Es de anotar que si se decide construir un intervalo de confianza para
todos los posibles valores de X, se obtendrán las bandas de confianza
del $100(1-\alpha)\%$ para la respuesta media $\beta_0+\beta_1x_i$
Predicción de nuevas observaciones
Suponga que $x_0$ es un valor de interés que para predecir, entonces
para obtener un valor único $y_0$, podremos utilizar la fórmula de la
recta de regresión tal que, al igual que en el caso de la respuesta
media la estimación puntual media de $Y$ dado $x_0$
\begin{align*} \hat{y_0}= \hat{\mathbb{E}}(Y|x_0)= \hat{\beta}_0 + \hat{\beta}_1 x_0 \end{align*}
Pero en este al ser un valor predicho tendremos que estimar la varianza
de la diferencia $\hat{y}_0 - y_0$, la cual tiene una media
\begin{align*} \mathbb{E}(\hat{y_0} - y_0) &=\mathbb{E}[\hat{\beta}_0+\hat{\beta}_1x_0] - (\beta_0 + \beta_1 x_0 +\varepsilon)] = 0 \end{align*}
y varianza
\begin{align*} Var(\hat{y_0} - y_0) &= \sigma^2\left[\frac{1}{n} + \frac{(x_0 - \bar{X})^2}{S_{xx}}\right] + \sigma^2\\ &=\sigma^2\left[1 + \frac{1}{n} + \frac{(x_0 - \bar{X})^2}{S_{xx}}\right]\\ &=\hat{\sigma}^2_e\left[1 + \frac{1}{n} + \frac{(x_0 - \bar{X})^2}{S_{xx}}\right]\\ \end{align*}
Entonces, un intervalo de confianza del $100(1-\alpha)\%$ para un
valor predicho $y_0$, se puede construir de la forma
\begin{align*} y_0 \pm t_{\frac{\alpha}{2}, n-2} \sqrt{\hat{\sigma}^2_e\left[1+\frac{1}{n}+ \frac{(x_0 - \bar{X})^2}{S_{xx}}\right]} \end{align*}
Es de anotar que si se decide construir un intervalo de confianza para
todos los posibles valores de X, se obtendrán las bandas de confianza
del $100(1-\alpha)\%$ para la predicción individual.