
La estadística en la evaluación socioeconómica de proyectos
La evaluación socioeconómica de proyecto es una herramienta de planeación que busca identificar, cuantificar y valorar los costos y beneficios generados por un proyecto en el bienestar de la sociedad y determinar el efecto y la rentabilidad de las inversiones sobre la población afectada por el proyecto, con el fin de decidir mediante juicios objetivos y técnicos la conveniencia de ejecutar dicho proyecto.
Thomas, Vidal, & Chacur (2008, p. 51) señala que para decidir si un proyecto es o no rentable en términos del ingreso nacional debe observarse los beneficios y los costos sociales anuales brutos del proyecto, en donde el primero se mide mediante el aumento que dicho proyecto provoque en el ingreso nacional, mientras que el segundo se mide mediante el ingreso nacional sacrificado por el hecho de haber efectuado este proyecto en lugar de otro, en donde el objetivo será que la rentabilidad del proyecto sea mayor o igual que el obtenido al ejecutar un proyecto alternativo.
Es aquí donde el análisis estadístico toma relevancia dentro de la evaluación de proyectos, puesto que, permite al investigador realizar análisis cualitativos o cuantitativos dentro de la gestión de un proyecto para la toma de decisiones, ya que al emplear herramientas estadísticas éste puede cuantificar el riesgo y la incertidumbre que tiene un proyecto, además de permitirle calcular diferentes probabilidades asociadas a partir de distribuciones de probabilidad.
Introducción a la Estadística
La Estadística es una herramienta ampliamente utilizada en diferentes disciplinas científicas, debido a su gran potencial para recolectar, analizar, interpretar, estimar y presentar de forma amigable, la información que se genera en las distintas áreas del conocimiento, para así poder argumentar y soportar de mejor manera las investigaciones realizadas, y/o mejorar los resultados obtenidos en la toma de decisiones.
Adicionalmente, la estadística tiene como ventaja respecto a otras áreas, que permite extraer información de variables tanto númerica como categórica de la población de interés o de una muestra de la misma, permitiendo al investigador establecer conclusiones acerca de la misma población, o de alguno de los parámetros que la conforman. Y es debido a ésto, que puede considerarse a la estadística como uno de los pilares fundamental dentro de la investigación científica teórica y aplicada.
En general, el análisis estadístico puede dividirse en dos partes:
- La Estadística descriptiva, la cual se encarga de resumir la información suministrada mediante el empleo de tablas, gráficas y medidas numéricas, junto con el análisis de las mismas, para facilitar la interpretación y la presentación de la información.
- La Inferencia estadística, la cual se encarga de la inferencias, modelamiento y predicción de la información, para facilitar la obtención de conclusiones y toma decisiones.
Estadística descriptiva
En general, la importancia del análisis estadístico radica en la resolución de problemas vinculados con datos, en donde la variabilidad de los mismos es quién guiará la importancia del empleo de diferentes técnicas para el manejo de la información. Desde este punto de vista, se discute en esta sección sobre la implementación de resúmenes de información, así como la presentación por medio de cuadros, diagramas o gráficos, cálculo y uso de medidas estadísticas de tendencia central, localización, variabilidad y forma.
Un aspecto importante a tener en cuenta al realizar análisis estadísticos, es señalado por Esquivel (2016, p. 29), el cual menciona que dentro de un análisis con información estadística, se debe tener en cuenta las siguientes etapas:
- Leer entre los datos: que consiste en llevar a cabo una lectura literal de la información, sin interpretar su contenido.
- Leer dentro de los datos: implica no solamente interpretar los datos sino integrarlos dentro del contexto.
- Leer más allá de los datos: significa tomar los datos como referente para identificar patrones que transciendan el grupo de datos observado, ya sea mediante la interpolación o extrapolación de resultados.
- Leer detrás de los datos: consiste en llevar a cabo un análisis crítico de la información que se estudia, esto implica analizar integralmente el problema, desde su origen, el tipo de dato que se utiliza, su validez y fiabilidad para analizar el problema y la posibilidad de generalizar los hallazgos.
Tipos de datos
En términos generales, los datos son cualquier pieza de información recolectada del fenómeno que se pretende analizar, y que, dependiendo de las características que posean, deben clasificarse dentro de una determinada categoría.
En términos generales, los datos son cualquier pieza de información recolectada del fenómeno que se pretende analizar, y que, dependiendo de las características que posean, deben clasificarse dentro de una determinada categoría junto a una determinada escala de medición.
- Cuantitativos: Son datos que pueden ser medidos o cuantificados.
Estos se subdividen en dos categorías:
- Discretos: Son aquellos datos que provienen de procesos que involucran conteos, y por tanto, solo pueden tomar valores enteros. Por ejemplo: Edad de una persona, número de estudiantes que perdieron un curso, cantidad de profesores que dictan seminarios
- Continuos: Son aquellos datos que provienen de procesos que involucran mediciones, y por tanto, solo pueden tomar cualquier valor real dentro de un intervalo. Por ejemplo: Temperatura de congelación del agua, Tiempo que dura una clase, Utilidad diaria de un negocio.
- Cualitativos: Son datos asociados a una cualidad o propiedad, y
por tanto, no pueden representarse numéricamente, a pesar de poder
caracterizarse alfanúmericamente.
- Nominal: Son aquellos factores que establecen etiquetas o categorías a los datos, sin estar sujetos a un orden específico. Por ejemplo: Partido político, Comuna de residencia, Tipo de animales en una granja
- Ordinal: Son aquellos factores que establecen etiquetas o categorías a los datos, junto a una estructura jerárquica. Por ejemplo: Estrato socioeconómico, Nivel de una enfermedad, Grado de escolaridad
Medidas estadísticas
Las medidas estadísticas tienen por objetivo resumir la información contenida en un conjunto de datos, en pocos valores numéricos que representan diferentes características. Estas medidas estadísticas nos darán información sobre la situación, dispersión, forma, asociación que posee un conjunto de datos de manera que sea posible captar rápidamente la estructura de los mismos.
Caso de estudio
Suponga que se está interesado en la construcción de una nueva vía
sur-norte cerca a la avenida Guayabal con el objetivo de reducir el
tráfico en dicha vía y la autopista Sur, y para ello se decide registrar
entre otras variables, el número de vehículos que transitan dicha vía
por día, tomando de referencia un total de $28$ días para realizar los
análisis, obteniendo los siguientes resultados
| 1142 | 1430 | 1005 | 1538 | 1116 | 1537 | 1307 | 1510 | 1522 | 1310 |
| 1088 | 1166 | 1365 | 1391 | 1195 | 1737 | 1452 | 1596 | 1588 | 1248 |
| 1097 | 1142 | 1365 | 1542 | 1609 | 1220 | 1260 | 1588 |
Otra variable de interés registrada para estos (28) días, es la del
material particulado $2.5$ $PM_{2.5}$, con el objetivo de medir de
cierta manera la contaminación generada en estos días, obteniendo los
siguientes resultados
| 23.45 | 22.9 | 11.62 | 30.1 | 28.17 | 21.51 | 28.72 | 34.29 | 31.08 | 24.26 |
| 24.08 | 19.81 | 25.46 | 27.98 | 24.63 | 20.21 | 29.6 | 20.9 | 19.93 | 23.02 |
| 18.84 | 19.39 | 32 | 30.32 | 27.42 | 27.75 | 22.8 | 31.49 |
Finalmente se decide registrar la zona en la cual fueron tomados los anteriores registros cada día, con el objetivo de tener una variable de control que permita asociar el número de vehículos y el material particulado, pues esta variable podría servir para identificar cuál es la zona más concurrida, más contamiante, y la cual podría ser un buen sector para iniciar las obras.
| 1 | 2 | 3 | 5 | 3 | 5 | 3 | 1 | 3 | 4 |
| 4 | 3 | 4 | 5 | 3 | 4 | 5 | 5 | 1 | 1 |
| 3 | 3 | 1 | 2 | 4 | 2 | 5 | 4 |
Medidas de tendencia central
Estas medidas tienen por objetivo cuantificar el comportamiento central
de un conjunto de observaciones. Si se define $x_1, x_2, \ldots, x_n$
como un conjunto de $n$ observaciones, entonces
Media
Es el promedio numérico de las $n$ observaciones.
\begin{align*} \bar{X}=\sum_{i=1}^n\frac{x_i}{n} \end{align*}
En Excel, puede calcularse el valor promedio de un conjunto de
observaciones mediante la función PROMEDIO().
Ejercicio caso de estudio
Calcule el número promedio de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
A partir de los datos se tiene entonces que el número promedio de automóviles que transitan por la avenida Guayabal es de \[\begin{align*} \bar{X} &= \sum_{i=1}^n\frac{x_i}{n}\\ &= \frac{1142 + 1430 + 1005 + \ldots + 1588}{28} \\ &= 1359.5 \end{align*}\] Lo anterior significa que, el número promedio de datos transitan por la avenida Guayabal en un día es igual a \(1359.5\) automóviles.
Mediana
Es el valor que ocupa el lugar central en un conjunto de datos, es
decir, el valor que divide el conjunto de observaciones en dos partes
que contienen el $50\%$ de las observaciones. Para realizar el cálculo
de la mediana es necesario ordenar inicialmente el conjunto de
observaciones de forma ascendente.
\begin{align*} \tilde{X}=\begin{cases}x_{\left[\frac{(n+1)}{2}\right]} & \text{si } n \text{ es impar}\\\frac{1}{2}\left(x_{\left[\frac{n}{2}\right]}+x_{\left[\frac{n}{2}+1\right]}\right) & \text{si } n \text{ es par}\end{cases} \end{align*}
donde $x_{\left[j\right]}$ representa la $j$-ésima observación
ordenada.
En Excel puede calcularse la mediana de un conjunto de
observaciones mediante la función MEDIANA().
Ejercicio caso de estudio
Calcule la mediana obtenida del número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
Inicialmente, se observa que el número de días registrados fue de \(28\), por lo cual, se tiene que \(n\) es un número par, haciendo que la ecuación empleada sea \[\begin{align*} \tilde{X} &= \frac{1}{2}\left(x_{\left[\frac{n}{2}\right]}+x_{\left[\frac{n}{2}+1\right]}\right) \\ &= \frac{1}{2}\left(x_{\left[\frac{28}{2}\right]}+x_{\left[\frac{28}{2}+1\right]}\right) \\ &= \frac{1}{2}\left(x_{\left[14\right]}+x_{\left[15\right]}\right) \end{align*}\] En donde se observa que debe localizarse la observación que ocupa la posición número \(14\) y \(15\) en los registros del número de vehículos que transitan por día luego de ordenarlas de menor a mayor. Realizando el ordenamiento se tendrá que
| 1005 | 1088 | 1097 | 1116 | 1142 | 1142 | 1166 | 1195 | 1220 | 1248 |
| 1260 | 1307 | 1310 | 1365 | 1365 | 1391 | 1430 | 1452 | 1510 | 1522 |
| 1537 | 1538 | 1542 | 1588 | 1588 | 1596 | 1609 | 1737 |
donde se observa que las observaciones \(14\) y \(15\) para el número de
vehículos que transitan sur-norte por la avenida Guayabal es
\(x_{[14]}=1365\) y \(x_{[15]}=1365\), respectivamente.
Con
dichos valores se realiza entonces, el cálculo de la mediana, tal que
De lo anterior se obtiene que el \(50\%\) inferior de los días transitan por la avenida Guayabal sur-norte a lo más \(1365\) vehículos, mientras que el \(50\%\) superior de los días transitan por la avenida Guayabal sur-norte al menos \(1365\) vehículos.
Moda
Es el valor que ocurre con mayor frecuencia en un conjunto de datos, es decir, es la observación que se repite con mayor frecuencia. Es de anotar que en un conjunto de observaciones, se puede tener más de una moda, en cuyo caso se dirá que el conjunto de datos es bimodal, trimodal o multimodal.
En Excel puede calcularse la moda de un conjunto de
observaciones mediante la función MODA.UNO() para calcular el valor
que más se repite, o la función MODA.VARIOS() para calcular una lista
con los valores que más se repiten para el caso bimodal, trimodal o
multimodal, guardando la función con la secuencia
Ctrl+Shift+Enter.
Ejercicio caso de estudio
Calcule la moda del número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
Para encontrar el número modal de automóviles, es necesario localizar el número de vehículos que más se repita por día. Con el fin de ilustrar cual es este valor, se presenta nuevamente la tabla ordenada con el número de vehículos que transitaron cada uno de los \(28\) días para facilitar su visualización.
| 1005 | 1088 | 1097 | 1116 | 1142 | 1142 | 1166 | 1195 | 1220 | 1248 |
| 1260 | 1307 | 1310 | 1365 | 1365 | 1391 | 1430 | 1452 | 1510 | 1522 |
| 1537 | 1538 | 1542 | 1588 | 1588 | 1596 | 1609 | 1737 |
De la tabla anterior, se observa que estamos ante una situación trimodal en la cual los valores \(1142\), \(1365\) y \(1588\) son el número de vehículos que más se repiten en para los días registrados, ya que estos se repiten dos veces en el conjunto de observaciones.
Medidas de localización
Estas medidas tienen por objetivo dividir un conjunto de datos ordenado
en partes iguales, entendidas estas como intervalos que contienen la
misma proporción de observaciones. Si se define
$x_{[1]}, x_{[2]}, \ldots, x_{[n]}$, como un conjunto de $n$
observaciones ordenadas en forma creciente, entonces
Percentil
Son los noventa y nueve valores $(j=1,2,\ldots,99)$, que dividen a
un conjunto de datos ordenados en cien partes iguales. Para ello, es
necesario calcular inicialmente una variable $h_j$ de posicionamiento
dado el cuartil $j$ de interés, tal que
\begin{align*} h_j = \frac{j(n-1)}{100} + 1 \quad \quad j=1,2,\dots,99 \end{align*}
y posteriormente, con éste valor se realiza el cálculo del cuartil de
interés
\begin{align*} P_j=x_{[\lfloor h_j\rfloor]} + \left((h_j - \lfloor h_j\rfloor) \times (x_{[\lfloor h_j\rfloor + 1]} - x_{\lfloor h_j\rfloor}) \right) \quad \quad j=1,2,\dots,99 \end{align*}
siendo $\lfloor h_j\rfloor$ el valor piso de $h_j$, es decir, el
entero de $h$ aproximando siempre hacia abajo.
En Excel puede calcularse el k-ésimo percentil de un conjunto
de observaciones mediante la función PERCENTIL.INC().
Ejercicio caso de estudio
Calcule el percentil \(95\) del número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
Para realizar el cálculo del percentil número \(j=95\), es necesario ordenar el número de automóviles que transitan por la avenida Guayabal por día, tal que
| 1005 | 1088 | 1097 | 1116 | 1142 | 1142 | 1166 | 1195 | 1220 | 1248 |
| 1260 | 1307 | 1310 | 1365 | 1365 | 1391 | 1430 | 1452 | 1510 | 1522 |
| 1537 | 1538 | 1542 | 1588 | 1588 | 1596 | 1609 | 1737 |
Con los datos ordenados, se realiza el cálculo para la variable de posicionamiento \(h_j\), con \(j=95\), dado que se posee un total de \(28\) observaciones, tal que \[h_{95} = \frac{95(28-1)}{100} + 1 = 26.65\] Al reemplazar el valor obtenido en la variable de posicionamiento, en la formula de percentiles, con \(j=95\), obtenemos que \[\begin{align*}P_{95} &=x_{\lfloor h_{95}\rfloor} + \left((h_{95} - \lfloor h_{95}\rfloor) \times (x_{[\lfloor h_{95}\rfloor + 1]} - x_{\lfloor h_{33}\rfloor}) \right) \\ &= x_{\lfloor 26.65\rfloor} + \left((26.65 - \lfloor 26.65\rfloor) \times (x_{[\lfloor v\rfloor + 1]} - x_{\lfloor 26.65\rfloor}) \right) \\ & = x_{[26]} + \left((26.65 - 26) \times (x_{[26+1]}-x_{[26]})\right) \\ &= x_{[26]} + \left(0.65 \times (x_{[27]}-x_{[26]})\right)\end{align*}\] En donde, \(x_{[26]}=1596\) y \(x_{[27]}=1609\), son las notas que ocupan la posición \(26\) y \(27\) en el conjunto de datos ordenados para el número de automóviles que transitan por la avenida Guayabal en un día. Finalmente, al reemplazar dichos valores en la ecuación de percentiles se tendrá que \[\begin{align*} P_{95} &= 1596 + \left(0.65 \times (1609-1596)\right)\\ P_{95} &= 1604.45 \end{align*}\] De lo anterior, se podrá concluir que el \(95\%\) inferior de los días transita una cantidad de automóviles menor o igual a \(1604.45\), mientras que el \(5\%\) superior de los días transita una cantidad mayor o igual a \(1604.45\).
Medidas de dispersión
Estas medidas tienen por objetivo determinar la dispersión o
variabilidad que posee un conjunto de observaciones, en donde, entre
mayor sean estas medidas, mayor será el grado de dispersión de los
datos. Si se define $x_1, x_2, \ldots, x_n$ como un conjunto de $n$
observaciones, entonces
Varianza
Mide la distancia media al cuadrado del conjunto de datos respecto a
la media
\begin{align*} S^2=\frac{1}{n-1}\sum_{i=1}^n{(x_i-\bar{X})^2} \end{align*}
En Excel puede calcularse la varianza de un conjunto de
observaciones mediante la función VAR.S().
Ejercicio caso de estudio
Calcule la varianza para el número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
Para realizar el cálculo de la varianza del número de automóviles que transitan por la avenida Guayabal por día, se emplea la fórmula de la varianza en donde se observa que se requiere el número promedio de automóviles, en donde se emplea el valor de la media \(\bar{X}=1359.5\), tal que \[\begin{align*} S^2 &= \frac{1}{n-1}\sum_{i=1}^n{(x_i-\bar{X})^2} \\ &= \frac{1}{28-1}\left[(1142 - 1359.5)^2 + \ldots + (1220 - 1359.5) ^2\right] \\ &= 39226.6296296 \end{align*}\] Es de anotar, que la interpretación de la varianza no tiene mucho sentido, debido a que la unidad de medición estará elevada al cuadrado, así que en general, los valores calculados se usan para realizar el cálculo de la desviación estándar.
Desviación estándar
Es la raíz cuadrada de la distancia media del conjunto de datos respeto
a la media, es decir, indica qué tan dispersos se encuentra el conjunto
de observaciones de su valor promedio.
\begin{align*} S=\sqrt{S^2} \end{align*}
En Excel puede calcularse la desviación estándar de un conjunto
de observaciones mediante la función DESVEST.M().
Ejercicio caso de estudio
Calcule la desviación estándar para el número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
La desviación estándar para el número de automóviles que transitan por la avenida guayaban en un día, puede ser calculada de forma simple mediante la raíz cuadrada de la varianza, que se calculó anteriormente, obteniendo que \[\begin{align*} S &= \sqrt{S^2} \\ &= \sqrt{39226.6296296} \\ &= 198.0571373 \end{align*}\] En donde, de los resultados obtenidos se tiene que, la dispersión que poseen los datos respecto a su valor promedio es de \(198.0571373\) para el número de automóviles que transitan la avenida Guayabal en un día. Esto quiere decir, que el número promedio de automóviles que transitan la avenida es de \(1359.5\) con una desviación estándar de \(198.0571373\).
Coeficiente de variación
Es la desviación estándar como un porcentaje de la media aritmética de
un conjunto de datos. Sirve para observar el grado de variabilidad que
tiene un conjunto de observaciones respecto a su promedio
\begin{align*} CV = \frac{S}{|\bar{X}|} \times 100\% \end{align*}
Entre las funciones base de Excel no hay ninguna función que
calcule el coeficiente de variación de un conjunto de observaciones de
forma directa, pero éste es fácil de calcular mediante el empleo de la
desviación estándar $S$ y el valor absoluto de la media $\bar{X}$,
los cuales pueden calcularse mediante las funciones DESVEST.M() y
PROMEDIO(), respectivamente.
Ejercicio caso de estudio
Calcule la desviación estándar para el número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
El coeficiente de variación refleja la variación porcentual que tiene un conjunto de observaciones respecto a su valor promedio, por tanto, al aplicar la ecuación del coeficiente de variación al número de automóviles que transitan por la avenida Guayabal en un día, se tiene que \[\begin{align*} CV &= \frac{S}{|\bar{X}|} \\ &= \frac{198.0571373}{|1359.5|} \times 100\% \\ &= 14.5683808 \% \end{align*}\] De lo anterior, se aprecia que la variación porcentual del número de automóviles en un día no es muy alto respecto a su media ya que el porcentaje de variación asciende solo hasta el \(14.5683808 \%\) y por tanto se tendrá que los datos no se encuentran muy dispersos respecto a su media.
Rango intercuartílico
Es la distancia o amplitud que hay entre el percentil $25$ y percentil
$75$, de un conjunto de datos. Éste muestra la amplitud del $50\%$
de los datos centrales de un conjunto de observaciones. Esta medida
puede ser tomada como una medida de variabilidad para la mediana.
\begin{align*} IQR = P_{75} - P_{25} \end{align*}
Entre las funciones base de Excel no hay ninguna función que
calcule el rango intercuartílico de un conjunto de observaciones de
forma directa, pero éste es fácil de calcular mediante el empleo del
percentil $75$ $P_{75}$ y percentil $25$, $P_{25}$, los cuales
pueden calcularse mediante la función PERCENTIL.INC().
Ejercicio caso de estudio
Calcule el rango intercuartílico para el número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
El rango intercuartílico se calcula mediante la diferencia de los
percentiles del \(75\%\) y del \(25\%\), y por ello se hace necesario
realizar el cálculo de dichos valores.
Entonces, al realizar el cálculo de los dos percentiles con la formula
anteriormente presentada se encontrará que \(P_{75}=1537.25\), mientras
que, \(P_{25}=1187.75\), y por tanto, al reemplazar en la formula del
rango intercuartílico se tendrá que \[\begin{align*}
IQR &= P_{75} - P_{25} \\
&= 1537.25 - 1187.75 \\
&= 349.5
\end{align*}\]
Mostrando que, al eliminar el \(50\%\) de los datos más extremos, se
obtiene un rango intercuartil de \(349.5\) para el número de vehículos
que transitan por la avenida Guayabal en un día.
Desviación absoluta mediana
Es una medida de la dispersión de un conjunto de observaciones respecto a su mediana
\begin{align*} MAD=b\times Me(|X_i-\tilde{X}|) \end{align*}
donde $b$ es una constante definida como $b=1/C_{3}$, con $C_{3}$
el valor del tercer cuartil de la distribución de interés (no el
obtenido de los datos) y con $Me(|X_i-\tilde{X}|)$ la mediana del
valor absoluto de la diferencia $X_i-\tilde{X}$. Además, si la
distribución es normal, entonces $b\approx1.4826$.
Entre las funciones base de Excel no hay ninguna función que
calcule la desviación absoluta mediana de un conjunto de observaciones
de forma directa, pero éste es fácil de calcular mediante el empleo de
las funciones para la mediana MEDIANA() y valor absoluto ABS().
Ejercicio caso de estudio
Calcule la desviación absoluta mediana del número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
Para realizar el cálculo de la desviación absoluta mediana para el número de vehículos que transitan por la avenida Guayabal en un día, es necesario inicialmente realizar el cálculo de \(|X_i-\tilde{X}|\) para cada uno de los días registrados, siendo \(\tilde{X}=1365\) el valor de la mediana calculada previamente. Entonces al realizar el cálculo de la diferencia absoluta y ordenando de mayor a menor se obtienen los siguientes datos
| 0 | 0 | 26 | 55 | 58 | 65 | 87 | 105 | 117 | 145 |
| 145 | 1307 | 170 | 172 | 173 | 177 | 199 | 223 | 223 | 223 |
| 223 | 231 | 244 | 249 | 268 | 277 | 360 | 372 |
Seguidamente, se realiza el cálculo de la mediana de los valores
obtenidos en la tabla anterior, en donde, dado que se tienen \(28\)
observaciones, entonces \(Me(|X_i-\tilde{X}|)\) para el número de
vehículos que transitan por la avenida Guayabal en un día es igual a
\[\begin{align*}
Me(|X_i-\tilde{X}|) &= \frac{1}{2}\left(|X_i-\tilde{X}|_{\left[\frac{n}{2}\right]}+|X_i-\tilde{X}|_{\left[\frac{n}{2}+1\right]}\right) \\
&= \frac{1}{2}\left(|X_i-\tilde{X}|_{\left[\frac{28}{2}\right]}+|X_i-\tilde{X}|_{\left[\frac{28}{2}+1\right]}\right) \\
&= \frac{1}{2}\left(|X_i-\tilde{X}|_{\left[14\right]}+|X_i-\tilde{X}|_{\left[15\right]}\right)
\end{align*}\]
donde se observa que las observaciones \(14\) y \(15\) para de la
diferencia absoluta respecto a la mediana es
\(|X_i-\tilde{X}|_{[14]}=172\) y \(|X_i-\tilde{X}|_{[15]}=173\),
respectivamente.
Con dichos valores se realiza entonces, el
cálculo de la mediana, tal que
\[\begin{align*}
Me(|X_i-\tilde{X}|) &= \frac{1}{2}(172+ 173) \\
&=172.5
\end{align*}\]
Ahora, al emplear este valor, y asumiendo que \(b=1.4826\), se tendrá
que la desviación absoluta mediana el número de vehículos que transitan
por la avenida Guayabal en un día es igual a
\[\begin{align*}
MAD &= b\times Me(|X_i-\tilde{X}|)\\
&= 1.4826 \times 172.5 \\
&= 255.7485
\end{align*}\] De lo anterior se obtiene que la mediana del número de
vehículo que transitan en un día por la avenida Guayabal sur-norte es de
\(1365\) vehículos, con una desviación absoluta mediana de \(255.7485\).
Medidas de forma
Estas medidas tienen por objetivo evidenciar si el conjunto de observaciones tiene o no una forma simétrica y observar su nivel de concentración.
Coeficiente de asimetría
Este valor permite identificar si el conjunto de datos se distribuye
uniformemente alrededor de las medidas de tendencia central.
\begin{align*} \gamma_1 = \frac{n}{(n-1)(n-2)}\frac{\sum_{i=1}^n{(x_i-\bar{X})^3}}{S^3} \quad \quad -\infty<\gamma_1<\infty \end{align*}
El signo de $\gamma_1$ indica la dirección de la asimetría.
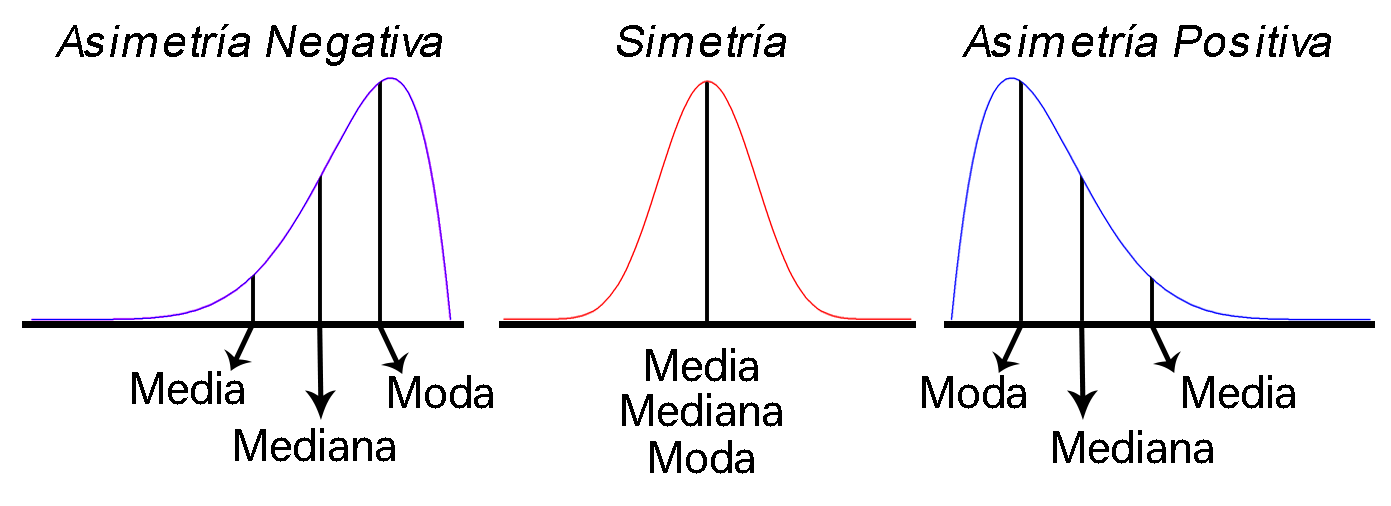
$\gamma_1>0$indica asimetría positiva, es decir, las observaciones se reúnen más en la parte izquierda de las medidas de tendencia central.$\gamma_1<0$indica asimetría negativa, es decir, las observaciones se reúnen más en la parte derecha de las medidas de tendencia central.$\gamma_1\sim0$indica simetría, es decir, existe aproximadamente la misma cantidad de observaciones a los dos lados de las medidas de tendencia central.
Representación tipos de Asimetría
En Excel puede calcularse la mediana de un conjunto de
observaciones mediante la función COEFICIENTE.ASIMETRIA().
Ejercicio caso de estudio
Calcule el coeficiente de asimetría del número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
El coeficiente de asimetría asociado al número de automóviles que transitan por la avenida Guayabal en un día depende del valor promedio \(\bar{X}= 1359.5\) y la desviación estándar \(S=198.0571373\). Por tanto al emplear los valores ya calculados previamente, se tendrá que el coeficiente de asimetría estará dado por \[\begin{align*} \gamma_{1} &= \frac{n}{(n-1)(n-2)}\frac{\sum_{i=1}^n{(x_i-\bar{X})^3}}{S^3}\\ &= \frac{28}{(27)(26)}\left[\frac{(1142 - 1359.5)^3 + \ldots + (1588 - 1359.5)^3}{198.0571373^3}\right] \\ &= -0.0106128 \end{align*}\] De lo anterior se observa que el coeficiente de asimetría es negativa pero cercana a \(0\), lo cual significa que el número de vehículos que transita por la avenida Guayabal en un día es aproximadamente simétrica con un leve sesgo hacia la izquierda, es decir, es un poco menos probable que ocurran valores inferiores a la media a que ocurran valores mayores.
Coeficiente de exceso de curtosis
Este valor permite observar el grado de concentración del conjunto de
datos
\begin{align*} \gamma_2 = \frac{n(n+1)}{(n-1)(n-2)(n-3)}\frac{\sum_{i=1}^n{(x_i-\bar{X})^4}}{S^4}-\frac{3(n-1)^2}{(n-2)(n-3)} \quad -2<\gamma_2<\infty \end{align*}
El signo de $\gamma_2$ indica el nivel de concentración.
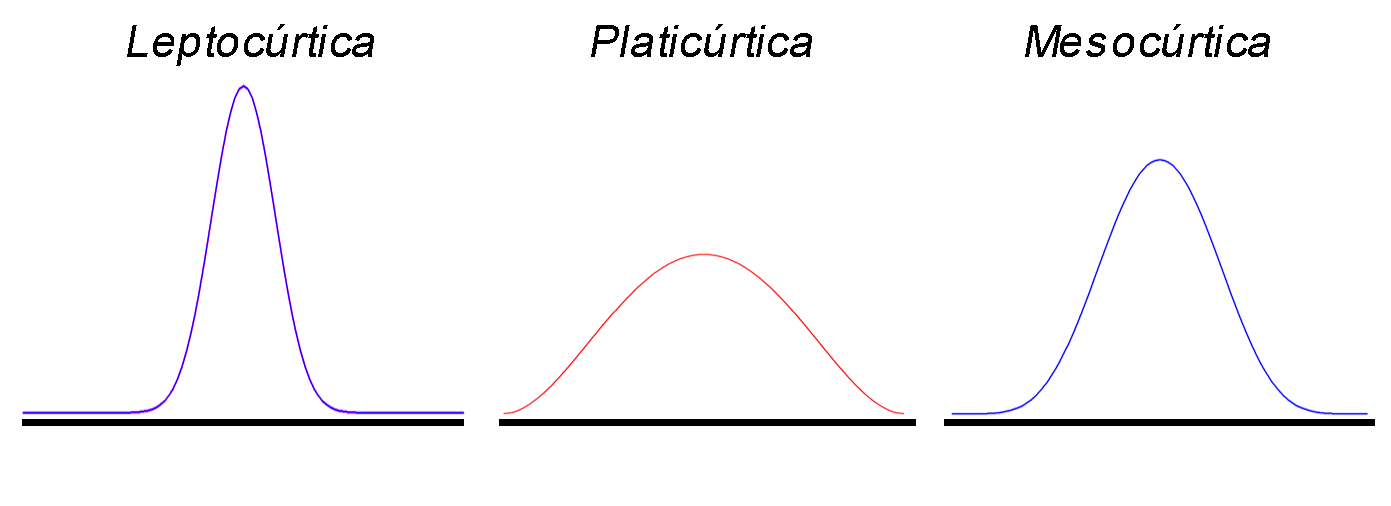
$\gamma_2>0$indica leptocurtosis, es decir, la forma de los datos es más en punta y posee colas menos anchas.$\gamma_2<0$indica platicurtosis, es decir, la forma de los datos es más plana y posee colas más anchas.$\gamma_2\sim0$indica mesocurtosis, es decir, tanto la punta como las colas son similares a la distribución normal.
Representación tipos de kurtosis
En Excel puede calcularse la mediana de un conjunto de
observaciones mediante la función CURTOSIS().
Ejercicio caso de estudio
Calcule el coeficiente de exceso de kurtosis del número de automóviles que transitan por la avenida Guayabal sur-norte en un día.
Solución
Similar al coeficiente de asimetría, el coeficiente de exceso de curtosis depende del valor promedio \(\bar{X}= 1359.5\) y la desviación estándar \(S=198.0571373\), del número de automóviles que transitan por la avenida Guayabal en un día, dando como resultado \[\begin{align*} \gamma_{2} &= \frac{n(n+1)}{(n-1)(n-2)(n-3)}\frac{\sum_{i=1}^n{(x_i-\bar{X})^4}}{S^4}-\frac{3(n-1)^2}{(n-2)(n-3)}\\ &= \frac{28(29)}{27}(26)(25)\left[\frac{(1142 - 1359.5)^4 + \ldots + (1142 - 1359.5)^4}{198.0571373^4}\right] - \frac{3(27)^2}{(26)(25)} \\ &= -1.1414707 \end{align*}\] A partir del valor calculado, se observa que el coeficiente de exceso de curtosis es menor que \(0\), y por tanto, se puede concluir que el número de automóviles que transitan por la avenida Guayabal en un día posee un comportamiento platicúrtico, es decir que el número de automóviles que transitan por día, poseen un comportamiento relativamente uniforme, debido a que su comportamiento es muy plano.
Medidas de asociación
Estas medidas tienen por objetivo estimar la magnitud con la que dos
fenómenos se relacionan, en donde, entre mayor sean estas medidas, mayor
será el grado de asociación que tendrán las variables. Si se define
$x_1, x_2, \ldots, x_n$ y $y_1, y_2, \ldots, y_n$ como dos conjuntos
de $n$ observaciones, entonces
Covarianza
Mide si existe o no dependencia lineal entre las variables, e indica el
grado de variación conjunta de dos variables respecto a sus medias
\begin{align*} S_{xy} = \frac{1}{n}\sum_{i=1}^n{(x_i-\bar{X})(y_i-\bar{Y})} \end{align*}
El signo de $S_{xy}$ indica el tipo de dependencia lineal que hay
entre las variables.
$S_{xy} > 0$indica que hay dependencia lineal positiva entre las variables, es decir, cuando aumenta una variable, la otra también aumenta.$S_{xy} < 0$indica que hay dependencia lineal negativa entre las variables, es decir, cuando aumenta una variable, la otra disminuye.$S_{xy} \approx 0$indica que no existencia dependencia lineal entre las dos variables.
En Excel puede calcularse la covarianza de dos conjunto de
observaciones mediante la función COVARIANZA.M().
Ejercicio caso de estudio
Calcule el covarianza que hay entre el número de automóviles que transitan la avenida Guayabal en un día y el \(CO_2\) generado en dichos días, para saber si existe o no dependencia lineal entre estas variables.
Solución
A diferencia de las anteriores medidas, el coeficiente de covarianza buscar observar si existe o no una dependencia lineal entre dos grupos de observaciones. Y para ello, se requiere los valores promedio asociados a las dos variables \(\bar{X}_{Vehículos}=1359.5\) y \(\bar{X}_{PM_{2.5}}=25.0617857\), obteniendo que la covarianza entre las variables es igual a \[\begin{align*} S_{Vehículos;\; PM_{2.5}} &= \frac{1}{n}\sum_{i=1}^n{(x_i-\bar{X})(y_i-\bar{Y})} \\ &= \frac{1}{28}\left[(1142-1359.5)(23.45- 25.0617857) + \ldots + (1588-1359.5)(31.49- 25.0617857)\right] \\ &= 391.427963 \end{align*}\] Dado que del coeficiente de covarianza, solo es posible interpretar el signo o cuando el valor está muy cercano a \(0\), se concluye entonces que existe una relación lineal positiva entre el número de vehículos que transitan por la avenida Guayabal y el material particulado \(2.5\) registrado en un día.
Correlación
Mide la fuerza de la dependencia lineal que hay entre variables, esta va
entre $-1$ y $1$
\begin{align*} \rho_{xy} = \frac{S_{xy}}{S_{x}S_{y}} \quad \quad -1<\rho_{xy}<1 \end{align*}
El valor de $\rho_{xy}$ indica el tipo y fuerza de la dependencia
lineal que hay entre las variables
$\rho_{xy} = 1$indica que existe dependencia lineal positiva exacta entre las variables, es decir, cuando aumenta una variable, la otra aumenta proporcionalmente en la misma cantidad. Este aumento es de la forma$Y = a + bX$, siendo$a$y$b$dos constantes, con$b>0$.$\rho_{xy} = -1$indica que existe dependencia lineal negativa exacta entre las variables, es decir, cuando aumenta una variable, la otra disminuye proporcionalmente en la misma cantidad. Este aumento es de la forma$Y = a + bX$con$a y b$dos constantes, y$b<0$.$\rho_{xy} = 0$No existe dependencia lineal entre las variables.
Además, se tendrá que si
$0.5 < \rho_{xy} \leq 1$fuerte correlación positiva entre$X$y$Y$.$0.3 < \rho_{xy} \leq 0.5$moderada correlación positiva entre$X$y$Y$.$0.1 < \rho_{xy} \leq 0.3$débil correlación positiva entre$X$y$Y$.$-0.1 \leq \rho_{xy} \leq 0.1$débil o ninguna correlación entre$X$y$Y$.$-0.3 \leq \rho_{xy} < -0.1$débil correlación negativa entre$X$y$Y$.$-0.5 \leq \rho_{xy} < -0.3$moderada correlación negativa entre$X$y$Y$.$-1 \leq \rho_{xy} < -0.5$fuerte correlación negativa entre$X$y$Y$.
En Excel puede calcularse la correlación de dos conjunto de
observaciones mediante la función COEF.DE.CORREL().
Ejercicio caso de estudio
Calcule la fuerza de la correlación que hay entre el número de automóviles que transitan la avenida Guayabal en un día y el \(CO_2\) generado en dichos días, para saber si existe o no dependencia lineal entre estas variables.
Solución
Similar al coeficiente de covarianza, el coeficiente de correlación buscar si existe o no una dependencia lineal entre dos grupos de observaciones, pero a diferencia de éste, el coeficiente de correlación muestra la fuerza de dicha relación. Por tanto, para realizar el cálculo del coeficiente de correlación entre el número de vehículos que transitan la avenida Guayabal en un día y el \(CO_2\) registrado, es necesario emplear el valor del coeficiente de covarianza \(S_{Vehículos;\; PM_{2.5}} = 391.427963\) y las desviaciones estándar calculadas para cada variable \(S_{Vehículos}= 198.0571373\) y \(S_{PM_{2.5}}=5.1145233\), tal que \[\begin{align*} \rho_{xy} &= \frac{S_{xy}}{S_{x}S_{y}} \\ &= \frac{391.427963}{(198.0571373)(5.1145233)} \\ & = 0.386417 \end{align*}\] Del resultado anterior se concluye, que hay existe una correlación positiva moderada entre el número de vehículos que transitan por la avenida Guayabal y el material particulado \(2.5\) registrado en un día, es decir que cuando aumenta una variable, también aumenta en menor proporción la otra variable.
Referencias
Esquivel, E. (2016). La enseñanza de la estadı́stica y la probabilidad, más allá de procedimientos y técnicas. Cuadernos de Investigación y Formación En Educación Matemática, 21–31.
Thomas, M., Vidal, R., & Chacur, A. (2008). Evaluación socioeconómica de proyectos con el método de opciones reales. Revista Ingenierı́a Industrial, 7(2).